

| English version |
|
|
| Mit den Tasten "dB" und "Faktor" neben den Eingabefeldern wird entschieden, von wo aus umgerechnet wird. Damit ist festgelegt, in welchem Feld die Eingabe über den Zahlentasten erscheint. Mit den Tasten "Feldgröße" und "Energiegröße" wird bestimmt, ob entweder 20 dB (Feldgröße, z. B. Spannung oder Schalldruck) oder 10 dB (Energiegröße, z. B. Leistung oder Intensität) dem Faktor bzw. dem Verhältnis "10" entspricht. |
Die Formeln für Spannung und Leistung
und ihre Pegel-Berechnung
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Bei dBm wurde als Bezugsleistung P0 = 1 Milliwatt = 0.001 Watt ≡ 0 dBm festgelegt.
 |
 |
|
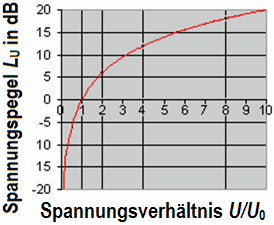
| Pegel der Feldgrößen |
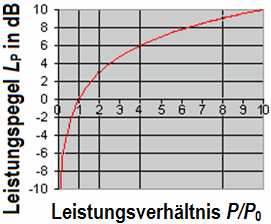
Pegel der Energiegrößen |
Schalldruck, Intensität und ihre Pegel
Umrechnungen und Berechnungen der Schallgrößen und ihre Pegel
Umrechnung: dBu in Volt, dBV in Volts, Volt in dBu und dBV
| Schallfeldgröße
Schalldruck, Schallschnelle, Amplitude, Schallauslenkung, Spannung, (Stromstärke, elektrischer Widerstand). Reziprokes Abstandsgesetz 1/r |
Schallenergiegröße Schallintensität, Schallenergiedichte, Schallenergie, Schallleistung, (elektrische Leistung). Reziprokes Quadratgesetz 1/r² |
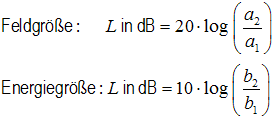
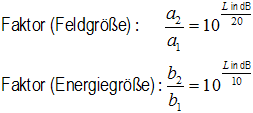
a1 bzw. b1 ist die jeweilige Bezugsgröße
a könnte z. B. eine Spannung U sein und b eine Leistung P. P ~ U2
| Schalldruck Schallfeldgröße |
Schalldruckpegel | 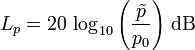 |
| Der Schalldruck p ist der Schallwechseldruck, der als Effektivwert angegeben wird und der dem statischen Druck pSt (Luftdruck) der umgebenden Luft überlagert ist. pges = pSt +p |
| Schallintensität Schallenergiegröße |
Schallintensitätspegel |
| Schallfeldgrößen: Schalldruck, Schallschnelle, Schallauslenkung, Amplitude. Feldgrößen, wie der Schalldruck werden immer als Effektivwert angegeben. Hierzu ist hauptsächlich die elektrische Spannung U proportional. Schallenergiegrößen: Schallintensität, Schallenergie, Schalll-Leistung, Schallenergiedichte. Hierzu ist hauptsächlich die elektrische Leistung P proportional. |
Abstandsgesetz für Feldgrößen und für Energiegrößen
| Lineare Feldgrößen, wie Volt und Schalldruck (dB-Wert) |
 |
| Die dazugehörende logarithmische Skala (Zahlenverhältnis) |
| Merke - Vergleich dB und dBA: Es gibt keine Umrechnungsformel von gemessenen dBA-Werten in Schalldruckpegel dBSPL oder umgekehrt. |
| Der Pegel der Ausgangsspannung ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 70,7% (Faktor = 0,7071), und der Pegel von −6 dB ist entsprechend 50% (= 1/2 = 0,5) der ursprünglichen Spannung. Dieses gilt für die Feldgröße Spannung bzw. Schalldruck. Der Pegel der Ausgangsleistung ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 50% (Faktor = 0.5) und der Pegel von −6 dB ist entsprechend 25% (= 1/4 = 0,25) der ursprünglichen Leistung. Dieses gilt für die Energiegröße Leistung bzw. Schallintensität. Man sollte versuchen, dieses zu verstehen. |
| Schalldruck und Schalldruckpegel 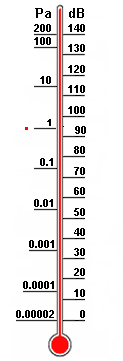 |
|
| Akustiker und Schallschützer ("Lärmbekämpfer") brauchen die Schall- intensität und die Schallleistung – jedoch benötigen Tontechniker und Sound-Designer ("Ohrenmenschen") diese Schallenergiegröße kaum. Daher sollte man sich eher um die Schallfeldgröße, den Schallwechseldruck kümmern und um den Pegel (Schalldruckpegel SPL) als Wirkung an den Trommelfellen des Gehörs und an den Membranen der Mikrofone, sowie der entsprechenden Audiospannung bzw. seinem Spannungspegel. |
| Leistung, ist wie alle Energiegrößen überwiegend eine berechnete Größe. |
|
In der analogen Tonstudiotechnik gibt es keine Leistungsanpassung. In Audio verwenden wir alleine Spannungsanpassung. |
| Die Bestimmungsgleichung für den Pegel von Feldgrößen (hier Spannung) ist: LU = 20 · log10(U/U0) in dB (Z1 = Z2), wobei U die zu messende Spannung und U0 der Bezugswert ist, zu dem U verglichen werden soll. Die Gleichung, um aus dem Pegel LU in Dezibel das Spannungsverhältnis U/U0 zu erhalten, ist U/U0 = 10(LU/20) Die Bestimmungsgleichung für den Pegel von Energiegrößen (hier Leistung) ist: LP = 10 · log10(P/P0) in dB, wobei P die zu messende Leistung und P0 der Bezugswert ist, zu dem P verglichen werden soll. Die Gleichung, um aus dem Pegel LP in Dezibel das Leistungsverhältnis P/P0 zu erhalten, ist: P/P0 = 10(LP/10) |
| Wir befassen uns mit der Tontechnik, also mit Audio und nicht mit Hochfrequenz (HF). Wir benötigen das Spannungsverhältnis, nicht das Leistungsverghältnis. Es stellt sich heraus, dass wenn man die gleiche Eingangs- und Ausgangsimpedanz hat, das Verhältnis der Spannungen somit exakt zwanzigmal der Logarithmus zur Basis zehn der Spannungsverhältnisse ausgedrückt werden kann. Wenn man eine Eingangsspannung von 0,1 Volt an einer 600-Ohm-Quelle hat und eine Spannung von 32 Volt an einer 600-Ohm-Last, dann ist die Spannungsverstärkung 20 × log 10 (32/0.1) = 20 x log (320 ) = 20 × 2,505 = 50 dB. Obwohl es nur korrekt ist, von Dezibel zu sprechen, wenn die Eingangs-und Ausgangs- Impedanz gleich ist, hat die Audio-Welt dieses (!) ignoriert, und wir sprechen von Spannungsverhältnissen ohne Rücksicht auf die Impedanz. Solch ein "Leistungsverstärker", der ein Eingangssignal von 1,5 V aus einer 1000-Ohm-Quelle benötigt, um eine Spannung von 30 Volt an 8 Ohm abzugeben, hat eine Verstärkung von 20 × log (30/1.5) = 20 × log (20) = 20 × 1,3 = 26 dB. Somit ist "dB" einfach eine andere Art ein Verhältnis zu schreiben. |
| Pegel-Änderung (dB) | Faktor-Änderung |
|---|---|
| 3 dB Anhebung ≡ | Doppelte Schallerergie:Faktor √2 |
| 3 dB Absenkung ≡ | Halbe Schallenergie: Faktor √0,5 |
| 6 dB Anhebung ≡ | Doppelter Schalldruck: Faktor 2 |
| 6 dB Absenkung ≡ | Halber Schalldruck: Faktor 0,5 |
| 10 dB Anhebung ≡ | Doppelte Lautstärke: Faktor 10 |
| 10 dB Absenkung ≡ | Halbe Lautstärke: Faktor 0,1 |
|
| Aus: http://www.bv-elbtal.de/html/was_ist_larm_.html |
| zurück |
Suchmaschine |
Startseite |