

| English version |
| Rechner mit freundlicher Genehmigung von DoctorProAudio.com Fülle das Feld oben aus und klicke auf die jeweilige Berechnungs-Taste darunter. Die Bezugs-Spannung für 0 dBu ist 0,775 Volt (0,77459667 V) und für 0 dBV sind es genau 1,0 Volt. Dabei ist V(eff) = V(RMS). Scrolle nach unten, um die dazugehörenden Formeln für Spannung und Leistung, sowie die Berechnung des absoluten Pegels zu finden. s-s = Spitze-Spitze. |
| Der Index bei dBu kommt von "u = unloaded" und bei dBV von "V = 1 Volt". Das "u" in dBu soll anzeigen, dass die Last "unspecified", also "unfestgelegt" oder "unabgeschlossen" sei und sie hochohmig ist. Was ist dBu? Ein log. Spannungsverhältnis mit einer Bezugsspannung von U0 = 0,7746 Volt ≡ 0 dBu Was ist dBV? Ein log. Spannungsverhältnis mit einer Bezugsspannung von U0 = 1,0000 Volt ≡ 0 dBV Der Homerecording-Pegel von −10 dBV bedeutet 0,3162 Volt, entsprechend −7,78 dBu Die 100%-Pegelmarke: +4 dBu für (USA) Pro Audio (1,228 V) oder +6 dBu für (ARD) Pro Audio (1,55 V) und −10 dBV (0,3162 V) für Consumer Audio (Heimtechnik). Der Verstärker-Maximalpegel nach ARD/IRT Pflichtenheft 5/3 ist +18 dBu; in USA ist der maximale unverzerrte Gain sogar +24 dBu. Heimtechnik mit einem Pegel von −10 dBV ist üblicherweise unsymmetrisch. Studiotechnik mit einem Pegel von +4 dBu = 0 VU ist immer symmetrisch. |
Skala: Pegel in dBu und dBV im Vergleich zur Spannung in V
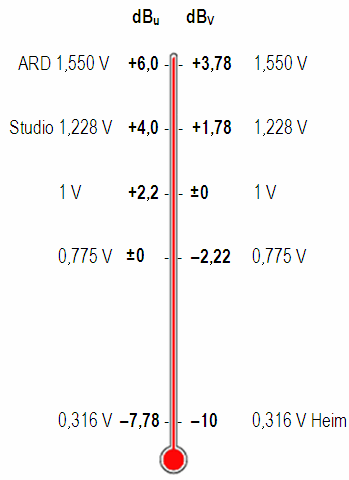 |
| Der Vollaussteuerungspegel 100% entsprechend +6 dBu (1,55 Volteff) ist der analoge Bezugspegel oder Referenzpegel vom IRT bzw. der ARD Rundfunk- und Fernsehanstalten. |
| Pegel in dBu |
Spannung in Volt |
Pegel in dBV |
|
| Studiopegel ARD | +6 | 1,550 | +3,78 |
| Studiopegel USA | +4 ● | 1,228 | +1,78 |
| Normpegel 1 Volt | +2,22 | 1 | 0 Bezug |
| Normpegel 0,775 Volt | 0 Bezug | 0,775 | −2,22 |
| Heimtechnik | −7,78 | 0,316 | −10 ● |
| Die Pegeldifferenz zwischen dem +4 dBu Studiopegel und dem −10 dBV Heimpegel ist Δ L = 11,78 dB (12 dB). Die Pegeldifferenz zwischen dem dBu-Pegel und dem dBV-Pegel ist Δ L = 2,2 dB. 0 dBV entsprechen 2,2 dBu oder 0 dBu entsprechen −2,2 dBV. Die Umrechnung von Pegel L (dBu) in Spannung (Volt) ist U = 0,775 · 10(L/20). Die Umrechnung von Spannung U (Volt) in Pegel (dBu) ist L = 20 · log (U/0,775). |
| Alle Feldgrößen, wie z. B. die elektrische Wechselspannung oder der Schallwechseldruck werden immer als Effektivwert (RMS) angegeben, ohne dass das extra gesagt werden muss. |
| Wichtige Gleichung (rechts) für sinusförmige Spannungen oder Ströme, die bei ohmschen Lasten die Berechnungen vereinfacht. |
| Pegel | 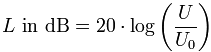 |
Spannung |
| Merke - Vergleich dB und dBA: Es gibt keine Umrechnungsformel von gemessenen dBA-Werten in Schalldruckpegel dBSPL oder umgekehrt. Auch ist eine Umrechnung von "dBA in Volt" and zurück nicht möglich. Berechnung ist nur bei Messung einer einzelnen Frequenz möglich. |
| Audiogeräte zeigen in ihren Datenblättern häufig A-bewertete Pegel – weil das mit unserem Gehör übereinstimmen würde − sondern weil damit beispielsweise Brummkomponenten versteckt werden können, die sonst ein Datenblatt schlechter aussehen lassen. Worte an helle Köpfe: Immer fragen, was ein Hersteller wohl zu verbergen hat, wenn die A-Frequenzbewertung angegeben wird. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
Wir verwenden keine dBm in der Tontechnik. Das gehört zur Leistung, die hier |
![]()
Erklärung: Was ist "dBFS"? (Digital Audio)
dBFS - Der digitale Aussteuerungspegel
| Analoge Pegel und digitale Pegel sind unterschiedliche Welten. |
♦ Oft gepostete Fragen: "dBFS und dBu - Wie sind die Skalen zueinander?"
und "Kann mir bitte jemand helfen dBFS nach dBu umzurechnen?"
oder "0 dBFS entsprechen analog wieviel dB?"
Niemals sind analoge Signalpegel in Bezug auf dBFS auszudrücken.
Wenn dieses befolgt wird, dann wird man niemanden verwirren.
| Es gibt keinen dB- nach dBFS Umrechner Merke – Vergleich dBFS und dBu: Es gibt keine feste Norm, wie z. B. –20 dBFS = +4 dBu = 0 dBVU. Die digitale Spitzenwert-Skala passt nicht zur analogen Effektivwert-Skala. Das sind zwei unterschiedliche Welten. |
| dBu sind Volt - die man mit einem Voltmeter misst. Analog-Audio: positive and negative Spannung. dBFS ist dagegen eine binäre Zahl. Digital-Audio: Nullen und Einsen. |
|
There is no such thing as peak volts dBu *) Es gibt keine Pegel als Spitzen-Volt dBu It is incorrect to state peak voltage levels in dBu. Es ist falsch, Spitzenspannungspegel in dBu anzugeben. |
Alle dBFS müssen mit einem Minuszeichen anfangen. Es gibt nicht so etwas wie +6 dBFS.
Hier gibt es wirklich keinen genormten Bezugswert (Referenz). |
| Hinweis: Die Aussteuerungsrichtlinien der EBU mit −9 dBFS sind nicht anzuwenden, wenn man nicht gerade für die europäischen Rundfunk und Fernsehanstalten arbeitet. Wer seine CD-Master auf "digital" −9dBFS aussteuert, der sollte sich nicht über zu leise CDs wundern. Bis nach ganz oben sind wirklich nutzlos 9 dB freigelassen. |
| Das Thema zu dBFS: Headroom bzw. Aussteuerungsreserve (Übersteuerungsreserve) Siehe dort ganz unten die Ergänzung von Eberhard Sengpiel. |
| Weitere empfehlenswerte Artikel zum Thema "Lautheit und Aussteuerungspegel": 10 things you need to know about ... EBU R 128 - the EBU loudness recommendation Florian Camerer: Loudness On the way to nirvana - audio levelling with EBU R 128 Die komplizierte Diskussion ist noch lange nicht beendet: (radioforen.de) Aussteuerungstechnik im Rundfunk - fortgesetzte Falschinterpretationen |
| LUFS = Loudness Units relative to Full Scale Lautheits-Einheiten relativ zu digitalem Vollpegel. |
Die Formeln für Spannung und Leistung
und die Berechnung des absoluten Pegels
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Bei dBm wurde als Bezugsleistung P0 = 1 Milliwatt = 0,001 Watt ≡ 0 dBm festgelegt
Tabelle zur Umrechnung von Spannungs- und Leistungsverhältnis in Dezibel dB
Tabelle der Schalldruckpegel und der entsprechenden Schalldruck- und Schall-Intensitäts-Werte
Umrechnen von Faktor oder Verhältnis in Pegelwert (Dezibel dB)
Die Wellenform-Parameter einer "230 V Sinus-Wechselspannung" (Effektivwert) werden hier angegeben:
Effektivspannung, Scheitelspannung und Spannung Spitze-Spitze
| Durchschnitts-Spannung | Effektiv-Spannung (Ueff) | Scheitelspannung Us = (Û) | Spannung Spitze-Spitze (Uss) |
| 0 Volt | 230 Volt = Ueff = ~u | 325 Volt = √2 · Ueff = 0,5 · Uss | 650 Volt = 2 · √2 · Ueff = 2 · Us |
| 0 Volt | 117 Volt = Ueff = ~u | 165 Volt = √2 · Ueff = 0,5 · Uss | 330 Volt = 2 · √2 · Ueff = 2 · Us |
| Der Effektivwert Ueff einer Wechselspannung U(t) = U0 · f(t) ist so definiert, dass die effektive Gleichstromleistung Ueff2 / R = Ueff · Ieff an einem Ohmschen Widerstand der mittleren Ohmschen Leistung der vorliegenden Wechselspannung an demselben Widerstand entspricht. |
Der Scheitelfaktor (crest factor) beschreibt das Verhältnis von
Spitzenspannung Û zum Effektivwert der Spannung Ueff.
Die Effektivspannung Ueff wird oft vom Englischen her mit URMS bezeichnet.
RMS = root mean square = Quadratischer Mittelwert = Effektivwert.
Spannungsumrechnungen
| Spannung | Ueff = ~u | Us | Uss |
| Effektivwert RMS Ueff = | − | 0,7071 · Us | 0,3535 · Uss |
| Scheitelwert (peak) Us = | 1,414 · Ueff | − | 0,5000 · Uss |
| Spitze-Spitze-Wert Uss = | 2,828 · Ueff | 2.000 · Us | − |
Nach DIN-Norm soll der Spitze-Spitze-Wert jetzt Spitze-Tal-Wert genannt werden.
Unterschiedliche Spannungspegel
| Pegel | Pegel L in dB | Spannung (Effektivwert = RMS) | Voltage peak-to-peak |
| Europäischer Studiopegel - ARD Rundfunkpegel | +6 dBu | 1,55 V | 4,38 V |
| Internationaler Studiopegel - USA | +4 dBu | 1,228 V | 3,47 V |
| Heimtechnikpegel (Consumergeräte) | −10 dBV | 0,3162 V ≡ −7,78 dBu | 0,894 V |
| Schalldruckpegel (bei der Hörschwelle) | 0 dB | 2·10−5 Pa ≡ 0 dBSPL | 5,66×10−5 Pa |
| Bezugsstudiopegel re 0.775 Volt | 0 dBu | 0,7746 V | 2,19 V |
| Bezugsstudiopegel re 1 Volt | 0 dBV | 1,0000 V | 2,828 V |
Internationale Bezugswerte (Referenz)
| Physikalische Größe | Bezugswert | Pegeleinheit | Bemerkung |
| Spannung | U0 = 0,775 V | ≡ 0 dBu | Audio, NF-Technik, kein Impedanz-Bezug! |
| Spannung | U0 = 1 V | ≡ 0 dBV | Audio NF-Technik, USA |
| Spannung | U0 = 1·10−6 V | HF-Empfänger-Verstärker-Technik - Bezugswert 1 µV | |
| Spannung | U0 = 0,224 V | HF-Technik - Bezugswert 1 mW an R = 50 Ω | |
| Spannung | U = 1,55 V | Studiopegel +6 dBu, ARD - Bezugswert 0,7746 V | |
| Spannung | U = 1,228 V | Studiopegel +4 dBu, USA - Bezugswert 0,7746 V | |
| Spannung | U = 0,3162 V | Heimtechnikpegel −10 dBV - Referenz 1,0 V ≡ −7,78 dBu | |
| Schalldruck | p0 = 2·10−5 Pa | ≡ 0 dB | Hörschwelle ("Schallfeldgröße"), Sound Pressure Level SPL |
| Schallschnelle | v0 = 5·10−8 m/s | ≡ 0 dB | |
| Schallintensität | I0 = 1·10−12 W/m2 | ≡ 0 dB | Schmerzschwelle ("Schallenergiegröße") bei etwa 1 W/m2 |
| Leistung | P0 = 1 W | ≡ 0 dBW | Die Referenzimpedanz ist hierbei immer anzugeben |
| Leistung | P0 = 1 mW | ≡ 0 dBm | R = 600 Ω (Telefon) oder R = 50 Ω (Antenne) |
| Elektrische Feldstärke | E0 = 1·10−6 V/m |
| Dezibel (dB) Rechner Dezibel stellen den zehnfachen Logarithmus eines Leistungsverhältnisses dar. Das Dezibel wandelt Multiplikations- und Divisionsrechnungen in einfache Additions- und Subtraktionsrechnungen um. Dieser Rechner rechnet zwischen Dezibel, Spannungsverstärkung (oder Stromverstärkung) um. Einfach eine Zahl in ein Feld eingeben und der the Rechner wird die anderen beiden Felder ausfüllen. Gleichungen: Pegel in dB: L = 20 · log (V1/V2) = 10 · log (P1/P2) |
| Das dBm ist ein logarithmisches Leistungsmaß bezogen auf 1 mW; es ist also leistungsbezogen. Es kann in Spannung umgerechnet werden, wenn die Last (Impedanz) bekannt ist. Typisch sind als Last 600 Ohm oder 50 Ohm. Gleichung: Pegel in dBm: LP = 10 · log (P / 0,001) |
| Einfache Faustregel: Bei Arbeiten mit Leistung ist: 3 dB das Doppelte und 10 dB das 10-fache. Beim Arbeiten mit Spannung oder Strom ist: 6 dB das Doppelte und 20 dB das 10-fache. |
| Warum wird die Bandbreite und die Grenzfrequenz mit dem Pegel "−3 dB" angegeben? Warum nehmen wir immer 3 dB nach unten beim Pegel eines Filters? Halbwertsbreite = Full width at half maximum - FWHM. Das ist der Punkt, an dem die Energie (Leistung) auf den Wert ½ gesunken ist oder auf 0,5 = 50 Prozent der ursprünglichen Leistung als Energiegröße, entsprechend (−)3 dB = 10·log(0,5). Ein (−)3 dB Leistungsabfall ist ein Abfall um 50% auf 50%. Die Spannung ist dabei auf den Wert √(½) gesunken oder auf 0,7071 = 70,71 Prozent der ursprünglichen Spannung als Feldgröße, entsprechend (−)3 dB = 20·log(0,7071). Ein (−)3 dB Spannungsabfall ist ein Abfall um 29,29% auf 70,71%. |
| (−)3 dB bedeutet ½ (die Hälfte) der Leistung. Da die elektrische Leistung proportional zum Quadrat der Spannung ist, ergibt sich ein Wert von 0,7071 oder 70,71% der Durchlass-Spannung. √½ = 1/√2 = √0,5 = 0,7071. P ~ U2, also 0,5 ~ 0,70712. |
| Tontechniker und Sound-Designer ("Ohrenmenschen") verwenden gern die (Schall-)Feldgröße, darum heißt es: Die Grenzfrequenz eines Geräts (Mikrofon, Verstärker, Lautsprecher) ist diejenige Frequenz, bei welcher der Ausgangsspannungspegel auf einen Wert von (−)3 dB unter den Eingangsspannungspegel (0dB) gesunken ist. ● (−)3 dB entspricht dem Faktor √½ = 1/√2 = 0,7071. Das ist 70,71% der Eingangsspannung. Akustiker und Schallschützer ("Lärmbekämpfer") drücken dieses mit der (Schall-)Energiegröße etwas anders aus: Die Grenzfrequenz eines Geräts (Mikrofon, Verstärker, Lautsprecher) ist diejenige Frequenz, bei welcher der Ausgangsleistungspegel auf einen Wert von (−)3 dB unter den Eingangsleistungspegel (0 dB) gesunken ist. ● (−)3 dB entspricht dem Faktor ½ = 0,5. Das ist 50% der Eingangsleistung (die Hälfte). |
| Merke: Power gain - also Leistungsverstärkung - ist in der Audiotechnik (Tontechnik) nicht üblich. Selbst Leistungsverstärker für Lautsprecher verstärken keine Leistung. Sie verstärken die Audio-Spannung, welche die Schwingspule bewegt. |
| Schallfeldgröße
Schalldruck, Schallschnelle, Amplitude, Schallauslenkung, Spannung, (Stromstärke, elektrischer Widerstand). Reziprokes Abstandsgesetz 1/r |
Schallenergiegröße Schallintensität, Schallenergiedichte, Schallenergie, Schallleistung, (elektrische Leistung). Reziprokes Quadratgesetz 1/r² |
| Merke: Schallfeldgröße (Schalldruck p, elektrische Spannung U) ist nicht Schallenergiegröße (Schallintensität I, Schallleistung Pak). I ~ p2 bzw. P ~ U2. Bisweilen hört man auch die Aussage: Die Grenzfrequenz liegt dort, wo der Pegel L, um (−)3 dB gesunken ist. Was immer der Anwender uns damit genauer mitteilen will: Pegel ist Pegel oder dB ist dB. |
| zurück |
Suchmaschine |
Startseite |