Level calculator decibels converter dB calculator audio engineering impedance bridging matching thd percent % - sengpielaudio.com
 
Deutsche Version UK-flag s/w - sengpielaudio.com D-flag - sengpielaudio.com
 
How to calculate decibels? - dB calculator
● The decibel  calculator  (dB) - a valuable tool ●

dB
factor (ratio)
field size energy size
 
             

With "dB" and "ratio" near the input boxes, we decide what is
calculated and which box is the input.
With size of a "field" and size of "energy" we decide if it is 20
times (field quantity, e.g. volts) or 10 times (energy quantity, or
power quantity, e.g. watts) in the formula.
The bar changes plus and minus, when dB is chosen.
It makes the reciprocal, when factor (ratio) is chosen.

Room Modes - sengpielaudio.com

The formulas for voltage and power
and the level calculation

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Voltage V (audio) 
volts		  ↔  Voltage level LV (audio) 
dBu
Formula voltage   Formula voltage level
Reference voltage V0 = 0.7746 volt ≡ 0 dBu
Voltage V  
volts		  ↔  Voltage level LV 
dBV
Formula voltage   Formula voltage level
Reference voltage V0 = 1 volt ≡ 0 dBV
Electric power P  
watts		  ↔  Electric Power level LP 
dB
Formula power   Formula power level
Reference power P0 = 1 watt ≡ 0 dB

dBm indicates that the reference power is P0 = 1 milliwatt = 0.001 watt ≡ 0 dBm.

Electric power P (telephone)  
watts		  ↔  Electric Power level LP 
dBm
Formula power telephone   Formula power level
Reference power P0 = 1 milliwatt (mW) = 0.001 W ≡ 0 dBm
Voltage Ratio and Voltage Level - sengpielaudio.com            Power Ratio and Power Level - sengpielaudio.com
Level of field quantity
Formula Voltage		            Level of energy quantity
Formula power level

Sound pressure, sound intensity, and their levels:
Conversions and calculations of sound quantities and their levels

Sound field quantities    AnimatedLaughingSmiley
Sound pressure, sound or particle velocity,
particle displacement or displacement amplitude,
(voltage, current, electric resistance).
Inverse Distance Law 1/r		         Sound energy quantities
Sound intensity, sound energy density,
sound energy, acoustic  power.
(electrical power).
Inverse Square Law 1/r²

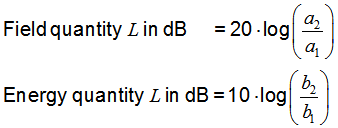
Pegel in dB

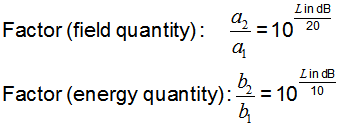
Faktor

a1 and b1 is the reference
'a' could be a voltage V and 'b' could be a power P.    P ~ V2

 Sound pressure 
 Sound field size		 Formula sound pressure           Sound pressure level  Formula sound pressure level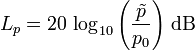

Reference sound pressure p0 = 20 μPa = 2 × 10-5 Pa ≡ 0 dB
Field sizes as the sound pressure, will always be shown as RMS value.
The sound pressure p is the sound pressure that is specified as an rms value and of the
static pressure pSt (air pressure) of the surrounding air is superimposed. ptotal = pSt + p

Sound intensity 
Sound energy size 		 Formula intensity  Sound intensity level  Formula intensity level
Reference sound intensity I0 = 1 × 10−12 W/m2 ≡ 0 dB

Sound field sizes: sound pressure, particle velocity, particle amplitude. Field sizes,
such as the sound pressure are always expressed in RMS.
This is mainly proportional to the electric voltage V.
Sound energy sizes: sound intensity, sound energy, sound energy density, acoustic power.
This is mainly proportional to the electric power P.

Decibel scale for linear field sizes, like volts and sound pressures
dB-Ratio - sengpielaudio.com
The logarithmic scale (ratio)

 
 Note - Comparing dB and dBA: There is no conversion formula for
 measured dBA values to sound pressure level dBSPL or vice versa. 
 

3 dB mean voltage related to a ratio of the factor √ 2 = 1.4142 or 1 / √ 2 = 0.7071.
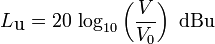
Voltage level

3 dB mean power (energy) related to a ratio with the factor 2 (doubling) or 0.5 (half).
Power level

 
The level of the output voltage level is 0 dB, that is 100% (factor or ratio = 1).
The level of −3 dB is equivalent to 70.7% (factor = 0.7071), and the level of
−6 dB is equivalent to 50% (factor = 1/2 = 0.5) of the initial voltage.
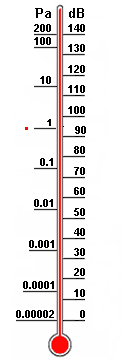This applies to the field quantity voltage or sound pressure.
 
The level of the output power level is 0 dB, that is 100% (factor or ratio = 1).
The level of −3 dB is equivalent to 50% (factor = 0.5) and the level of
−6 dB is equivalent to 25% (factor = 1/4 = 0.25) of the initial power.
This applies to the energy quantity power or sound intensity.
 
Try to understand this.
 

 Sound pressure and
 sound pressure level 

      sound pressure
Note: The radiated sound power (sound intensity) is the cause
and the sound pressure is the effect,
where the sound engineer is particularly interested in the effect.
The effect of temperature and sound pressure:
Sound pressure and Sound power – Effect and Cause.
 
 
Acousticians and sound protectors ("noise fighters") need the sound
intensity (acoustic intensity) – but sound engineers and sound
designers ("ear people") don't need that sound energy quantity.
 
Who is involved in audio engineering, should rather take care of the
sound field quantity, that is the sound pressure or the sound pressure
level (SPL) as an effect at the eardrums of our hearing and on the
membranes of the microphones and the corresponding audio voltage
and its voltage level.
 
 
If we are a technician checking the sound quality by listening with our hearing,
think of the sound waves that move our eardrums by the effect of the sound
pressure as sound field size. That is why there is the advice:
In sound recording try to avoid the use of sound power and sound intensity as
sound energy sizes.
 
How many decibels (dB) is the sound energy W = I×t×A in1 J = W×s?
This question is asked quite rare. For calculations we use more the sound
energy sizes: sound energy density, w orE = I / c in J/m3, sound intensity I =
Pac/A in W/m², and sound power Pac in W = J/s and their corresponding levels.
 
 
Acousticians and sound protectors ("noise fighters") need the sound
intensity (acoustic intensity) – but as a sound engineer and sound
designer ("ear people") you don't need that sound energy quantity.
 
Who is involved in audio engineering, should rather take care of the
sound field quantity, that is the sound pressure or the sound pressure
level (SPL) as an effect at the eardrums of our hearing and on the
diaphragms of the microphones and the corresponding audio voltage
and its voltage level.
 
 
Effect and Cause − Sound pressure and Sound power
 
Conversion of Factor or Ratio to Level Value (Decibels dB)
 
The human perception of loudness (Factor, Ratio, Gain)
 
Converting Decibel to Percentage (%) and Distortion to Decibel
 
 
Power is like all energy sizes primarily a calculated value.
 
 
 
In sound engineering there is no Power matching or Impedance matching.
In audio we use only Voltage bridging or high Impedance bridging.
 
 
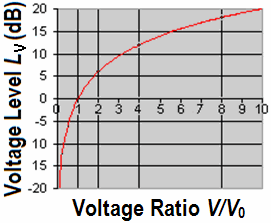
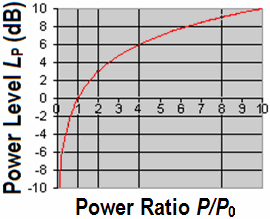
Charts: Conversion of voltage or power ratios to decibels dB
 
Decibel (dB) level conversion to volt
 
Conversion: Voltage V to Level dB, dBu, dBV, and dBm
 
The defining equation for the level in decibels for field sizes (here voltage) is:
LV = 20 × log10(V/V0)   (dB)      (Z1 = Z2)
where V is the voltage being measured, and V0 is the reference to which V is being compared.
 
The equation for obtaining voltage ratio V/V0 from the level LV in dB is:
V/V0 = 10(LV/20)
 
The defining equation for the level in decibels for energy sizes (here power) is:
LP = 10 × log10(P/P0)   (dB)
where P is the power being measured, and P0 is the reference to which P is being compared.
 
The equation for obtaining power ratio P/P0 from the level LP in dB is:
P/P0 = 10(LP/10)
 
We do audio, not RF.
We usually want to know VOLTAGE ratio, not POWER ratio.
 
It turns out that if we have the same impedance level for one voltage and another, the ratio of
the voltages can be accurately expressed as twenty times the log to base ten of the voltage
ratios.So if we have an input voltage of 0.1 V from a 600 ohm source, and we get an output
power of 32 V into a 600 ohms load, the voltage ratio is
20 × log 10 (32/0.1) = 20 × log (320) =
20 × 2.505 = 50 dB.
 
Although it is only correct to speak of decibels in instances where the input and output
impedances are the same, the audio world has ignored that (!), and we speak of voltage ratios
without regard to the impedance. So a "power amplifier" which needs an input of 1.5 V from a
1000 ohms source to give an output of 30 V into 8 ohms is spoken of as having a gain of
20 × log (30/1.5) = 20 × log (20) = 20 × 1.3 = 26 dB. So "dB" is simply another way to write
"ratio of".
 
Change in dB Change in factor
  3 dB increase  ≡  Sound energy doubled: factor √2
  3 dB decrease ≡  Sound energy halved: factor √0.5
  6 dB increase  ≡  Sound pressure doubled: factor 2
  6 dB decrease ≡  Sound energy halved: factor 0.5
10 dB increase  ≡  Loudness perception doubled: factor of 10
10 dB decrease ≡  Loudness perception halved: factor of 0.1
 
Loudness - Sound Pressure - Sound Intensity
 
From: http://www.bv-elbtal.de/html/was_ist_larm_.html
 
 
 
back weiter Search Engine zurück home start