

| English version |
Fülle das graue Feld oben aus und klicke auf die jeweilige Berechnen-Taste darunter.
1 Pascal = 1 Pa = 1 N/m2.
| Der atmosphärische Druck ist nicht das Gleiche wie der Schalldruck. Schalldruck oder Schalldruckpegel ist die lokale Druckänderung vom Mittelwert des Atmosphärendrucks verursacht durch eine Schallwelle. Der Schalldruck p ist der Wechseldruck, der dem statischen Luftdruck überlagert ist. Der Standard-Luftdruck ist 101 325 Pascal = 1 013,25 hPa = 101,325 kPa. ● 1 000 000 µPa = 1 Pa = 1 N/m2 ≡ 94 dBSPL (und 1 bar = 105 Pa) 20 000 000 µPa = 20 Pa = 20 N/m2 ≡ 120 dBSPL 1 µPa = 10−6 Pa = 10−6 N/m2 ≡ −26 dBSPL 1 kPa = 103 Pa = 1 000 Pa = 1 000 N/m2 ≡ 154 dBSPL SPL = Sound Pressure Level (SIL = Sound Intensity Level) |
| Schalldruck p (Effektivwert) als Schallfeldgröße: Die Hörschwelle wurde als Bezugsschalldruck p0 = 20 µPa = 2 · 10−5 Pa festgelegt. Sie entspricht bei f = 1 kHz dem Schalldruckpegel Lp = 0 dB. Schallintensität I als Schallenergiegröße: Die Hörschwelle wurde auch als Bezugsschallintensität I0 = 10−12 W/m2 berechnet. Sie entspricht bei f = 1 kHz dem Schallintensitätspegel LW = 0 dB. Schalldruck p = √ (I × Z0) Schallintensität I = p2 / Z0 Schallkennimpedanz Z0 = 400 N·s/m3 |
Was ist denn Schallpegel?
| Eine Reduktion des Schallleistungspegels der Schallquelle um 6 dB führt zu einer Reduktion des Schalldruckpegels und des Schallintensitätspegels am Ort des Empfängers von ebenfalls 6 dB, auch wenn die Schallleistung selbst auf den Faktor 0,25 – der Schalldruck aber auf den Faktor 0,5 und die Schallintensität auf den Faktor 0,25 abgefallen ist. DerReferenzwert (Bezugswert) für den Schallpegel wurde so gewählt, dass sich bei einer Schallkennimpedanz von Z0 = ρ · c = 400 N·s/m3 für den Schallintensitätspegel der gleiche Wert ergibt wie für den Schalldruckpegel. Wir sprechen daher einfach vom "Schallpegel" und lassen offen, ob Schalldruckpegel oder Schallintensitätspegel gemeint ist.
|
| Schalldruck und Schalldruckpegel 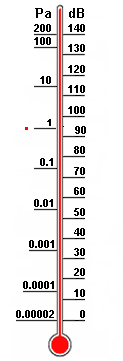 |
|
| Der Schalldruck (Wechseldruck) ist ein dynamischer Druck. Dagegen ist der Luftdruck (atmosphärischer Gleichdruck) ein statischer Druck. Dem statischen Luftdruck ist der dynamische Schalldruck überlagert. |
Schalldruck, Schallintensität und ihre Pegel
| Der folgende Rechner zeigt die häufig gewünschte direkte Umrechnung von Schalldruck in Schallintensität und zurück mit der Schallkennimpedanz von Luft Z0 = 400 N·s/m3. Der Schallpegel wird in dB (Dezibel) angegeben. |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Während der Schalldruckpegel in Luft mit dem Schallintensitätspegel übereinstimmt, wenn als Bezugs-Schallkennimpedanz Z0 = 400 N·s/m³ gewählt wird, ist das beim entfernungsunabhängigen Schallleistungspegel nicht der Fall. |
| Schalldruck und Schallleistung − Wirkung und Ursache |
| Hinweis: Da der Schallleistungspegel schwierig zu messen ist, misst man üblicherweise den Schalldruckpegel in dB. Eine Verdoppelung des Schalldrucks erhöht den Schalldruckpegel um 6 dB. |
| Subjektiv empfundene Lautstärke (Lautheit), objektiv gemessener Schalldruck (Spannung) und theoretisch berechnete Schallintensität (Schallleistung) |
| Psychoakustik: Zusammenhang zwischen sone und phon |
Schallpegeländerung und der Faktor (Gain)
Sei genau: Der doppelte Schalldruck, die doppelte Schallleistung oder die doppelte Schallintensität
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Schalldruckpegel und Schalldruck
| "Schallpegel" kann der Schalldruckpegel in dB-SPL oder der Schall-Intensitätspegel in dB-SIL sein. Für Pa sprich: Pascal. Das ist die Größe für den Druck p = Kraft F durch Fläche A. Der Bezugs-Schalldruck ist p0 = 20 µPa = 2 × 10−5 Pa. Die BezugsSchallintensität ist I0 = 10−12 W/m2. DAGA und auch DIN fordern die Angabe des Schallpegels allein in dB. Das angehängte SPL kommt aus USA und ist hier bei Akustikern verpönt. In Wikipedia wird das SPL hinter dB sofort beseitigt. Die häufig benutzte Bezeichnung "Intensität des Schalldrucks" ist nicht richtig. Dafür sind "Größe", "Stärke", "Kraft", "Wirksamkeit", "Amplitude", oder "Pegel" zu nehmen. "Schallintensität" ist Schallleistung pro Flächeneinheit, während "Druck" ein Maß für Kraft pro Flächeneinheit ist. Intensität als Energiegröße ist nicht gleich Druck als Feldgröße oder Quellengröße. |
Schalldruck ist nicht Intensität
| Unterscheide: Schalldruck p ist eine "Schallfeldgröße" und Schallintensität I ist eine "Schallenergiegröße". Selten wird dieses in der Lehre scharf genug getrennt und bisweilen sogar unrichtig gleichgesetzt. Aber I ~ p2. |
| Zu beachten ist, dass die Berechnung I ~ p2 für fortschreitende ebene Wellen seine Gültigkeit hat. Hieraus erkennt man, dass die Schallintensität niemals mit dem Schalldruck gleichgesetzt werden darf. Der Schalldruck ist immer der Schallwechseldruck als Effektivwert. Die Schalldruckamplitude ist der Scheitelwert oder Spitzenwert des Schalldrucks. Die Lautstärke (Lautheit) als psychoakustische Empfindung wird überwiegend durch den Schalldruck p bestimmt und als Schalldruckpegel Lp in dB angegeben. |
Pegel-Vergleich beim Schalldruck und bei der Schallintensität
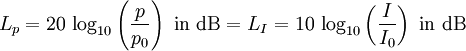 |
| Hinweis: Membranen der Mikrofone und die Trommelfelle unserer Ohren werden durch den Schallwechseldruck als Schallfeldgröße bewegt. Die Schallintensität ist jedoch eineSchallenergiegröße. |
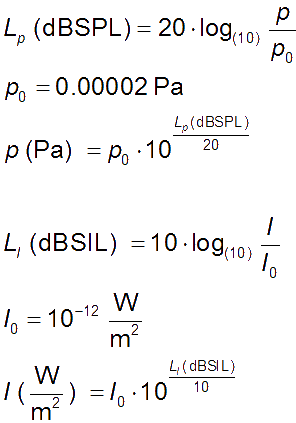
Bezugswerte (Hörschwelle): p0 = 20 µPa = 2 · 10−5 oder auch I0 = 10−12 Watt/m2.
| Schalldruck gehört zu den Schallfeldgrößen. Der Schalldruck nimmt mit 1/r von der Schallquelle ab! Das ist nicht reziprok und quadratisch, das ist umgekehrt proportional: p ~ 1 / r. |
|
| Intensität = Leistung / Fläche I = P/A = P/(4πr2) Pegeldämpfung ist 6 dB pro Abstandsverdopplung r |
| Abstandsdämpfung: Änderung des Schallpegels Δ L mit der Entfernung r Nachhilfe für alle, die falsch gelernt haben, dass der Schalldruck quadratisch mit der Entfernung abnimmt |
| Wenn bei einer Schallpegelmessung der Abstand zur Schallquelle nicht angegeben ist, dann ist das Messergebnis absolut sinnlos. Siehe z. B. "Schreiwettbewerb": http://homepages.fh-regensburg.de/~scs39082/wettbewerbe/schreiwettbewerb.html Merke: Je näher am Mund: umso mehr Pegel, umso lauter. Ist doch klar. ... und ohne dBA-Filter zeigen sich noch eindrucksvollere Pegelwerte. |
Vergleiche Schallleistungspegel und Schalldruckpegel im Abstand von der Quelle
Tabelle der Schalldruck- und Schallintensitätspegel
![]()
Schalldruck, Intensität und ihre Pegel
|
Schall unter Wasser siehe ganz unten.
| Von der Intensität des Schalldrucks zu sprechen ist Unsinn. Schalldruck und Schallintensität sind wirklich nicht das Gleiche. Missbrauche nicht das Wort "Intensität", es sei denn, hier ist wirklich die "Leistung pro Fläche" als W/m2 gemeint. Sage richtiger dafür "Größe", "Stärke" oder "Pegel". "Amplitude" gehört jedoch eher zu den Schallfeldgrößen. |
| Schallintensität = Schalldruck · Schallschnelle Schallintensität = (Kraft / Fläche) · (Schallauslenkung / Zeit) Schallintensität = Schallenergie/ (Fläche · Zeit) = Schallleistung / Fläche. I = p · v = (F / A) · (ξ / t) = E / (A · t) = Pak / A. |
| Merke - Vergleich dB und dBA: Es gibt keine Umrechnungsformel von gemessenen dBA-Werten in Schalldruckpegel dBSPL oder umgekehrt. |
| Die Hörschwelle bei 0 dB SPL ohne Frequenzbewertung kann bei breitbandigen Geräuschen nicht das Gleiche sein, wie 0 dBA mit Frequenzbewertung. Nur bei einem reinen Sinuston von 1 kHz sind beide Werte gleichzusetzen. Es gibt keine "dBA"-Angabe für die Hörschwelle beim menschlichen Hören. Bei weißem Rauschen im Audioband von 20 Hz bis 20 kHz soll der Unterschied zwischen dB und dBA etwa 2 dB betragen. |
| Audiogeräte zeigen in ihren Datenblättern häufig A-bewertete Pegel − nicht weil das mit unserem Gehör übereinstimmen würde − sondern weil damit beispielsweise Brummkomponenten versteckt werden können, die sonst ein Datenblatt schlechter aussehen lassen. Worte an helle Köpfe: Immer fragen, was ein Hersteller wohl zu verbergen hat, wenn die A-Frequenzbewertung angegeben wird. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
Schallmessung Bewertungsfilter - Berechnung Frequenz f in dBA
Wo liegt die Schmerzschwelle? Folgende runde Werte werden in der Audio-Literatur angegeben:
| Schalldruckpegel Lp |
Schalldruck p |
| 140 dBSPL | 200 Pa |
| 137,5 dBSPL | 150 Pa |
| 134 dBSPL | 100 Pa |
| 120 dBSPL | 20 Pa |
| Mit Schmerzgrenze, auch Schmerzempfindungsschwelle oder Schmerzschwelle, bezeichnet man in der Akustik die niedrigste Stärke eines Reizes, was vom Gehör als schmerzhaft empfunden wird. Solch ein Lärmpegel ist ganz gewiss schädlich. Wegen der unterschiedlichen Empfindlichkeit der Menschen kann kann es eben keine genaue Wertangabe geben. |
| Schalldruckpegel und zulässige Einwirkungszeit (Richtlinien) Wie lange kann jemand einen bestimmten Schallpegel aushalten, bevor ein Hörschaden eintritt? |
| Schalldruckpegel | Schalldruck | Erlaubte Einwirkungszeit |
| 115 dB | 11,2 Pa | 0,46875 Minuten (~30 sec) |
| 112 dB | 7,96 Pa | 0,9375 Minuten (~1 min) |
| 109 dB | 5,64 Pa | 1,875 Minuten (< 2 min) |
| 106 dB | 3,99 Pa | 3,75 Minuten (< 4 min) |
| 103 dB | 2,83 Pa | 7,5 Minuten |
| 100 dB | 2,00 Pa | 15 Minuten |
| 97 dB | 1,42 Pa | 30 Minuten |
| 94 dB − − − − − − − | 1,00 Pa − − − | 1 Stunde − − − − − − − − − − |
| 91 dB | 0,71 Pa | 2 Stunden |
| 88 dB | 0,50 Pa | 4 Stunden |
| 85 dB | 0,36 Pa | 8 Stunden |
| 82 dB | 0,25 Pa | 16 Stunden |
| Anerkannte Richtlinien für eine empfohlene zulässige Einwirkungszeit (Einwirkdauer) bei einer kontinuierlich zeitlich-gewichteten durchschnittlichen Lärmbelastung, nach NIOSH-AINSI und CDC. Für alle 3 dB Schalldruckpegel (SPL) über 85 dB ist die zulässige Einwirkungszeit jeweils halbiert, bevor Schäden am Gehör auftreten können. NIOSH = National Institute for Occupational Safety and Health CDC = Centers for Disease Control and Prevention. OSHA = Occupational Safety and Health Administration. NIOSH verwendet die 8-Stunden-Einwirkung von Rauschen bei 85 dBA und eine Verdopplungsrate von 3 dBA, um die Lärmdosis zu bestimmen. OSHA verwendet die 8-Stunden-Einwirkung von Rauschen bei 90 dBA und eine Verdopplungsrate von 5 dBA, die weniger Arbeitnehmer über ihre gesamte Lebensarbeitszeit schützt. Dieses stellt möglicherweise nicht die einzige weltweite Sichtweise dieses Themas dar. Lärm ist ein zunehmendes Problem für die öffentliche Gesundheit und kann folgende negativen gesundheitlichen Auswirkungen haben: Schwerhörigkeit, Schlafstörungen, Herz-Kreislauf- und psychophysiologische Probleme, Leistungsabfall und negatives sozialen Verhalten. Der Mensch empfindet und beurteilt Schallereignisse nach: Einwirkungsdauer, spektraler Zusammensetzung, zeitlicher Struktur, Schallpegel, Informationsgehalt und subjektiver Einstellung. |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Umrechnung: Schalldruck, Schallschnelle, Schallimpedanz und Intensität
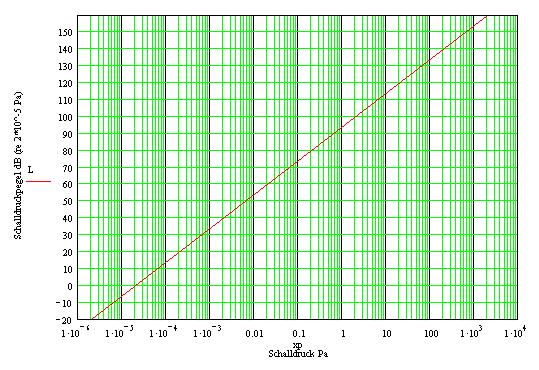
| Der Schalldruck p, als Schallfeldgröße, nimmt nach dem 1/r-Gesetz ab, während die Schallintensität I, als Schallenergiegröße nach dem 1/r²-Gesetz abnimmt. Das wird häufig nicht verstanden. Der Beweis dieses Fehlwissens ist hier zu sehen: |
| Schallfeldgröße
Schalldruck, Schallschnelle, Amplitude, Schallauslenkung, Spannung, (Stromstärke, elektrischer Widerstand). Reziprokes Abstandsgesetz 1/r |
Schallenergiegröße Schallintensität, Schallenergiedichte, Schallenergie, Schallleistung, (elektrische Leistung). Reziprokes Quadratgesetz 1/r² |
| Schall(wechsel)druck ist die Veränderung des Drucks verursacht durch eine Schallwelle. Schallleistung ist die Menge an Energie, die in einer Schallwelle enthalten ist. Es ist bedauerlich, dass die Begriffe "Leistung" und "Energie" in der Akustik vielfach verwechselt werden. Sie sind überhaupt nicht das Gleiche. Energie ist die Fähigkeit, etwas zu verrichten. Leistung ist die Menge an Energie, die pro Zeiteinheit verwendet wird. |
 |
Wichtig zu merken: 1 Pa = 1 N/m2 ≡ 94 dBSPL und
Unser Gehör ist direkt für den Schalldruck empfindlich. Der Schallwechseldruck bewegt |
1 bar = 105 Pa.
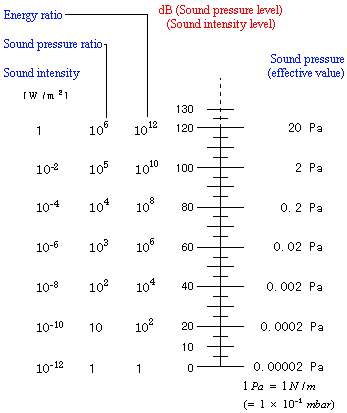 |
| Bei der Angabe eines absoluten Pegels zur Kennzeichnung des Schalldruckpegels wird immer häufiger der aus englischsprachigen Ländern kommende Zusatz "SPL" (sound pressure level) benutzt, z. B. 94 dBSPL. Diese Gewohnheit wurde hier manchmal übernommen. Beispiele: * Hörschwelle: 0,00002 Pa = 20 µPa = 2 · 10-5 Pa, entsprechend 0 dB (SPL) * Schmerzschwelle: etwa 150 Pa, entsprechend 137,5 dB (SPL) * "normal laut" empfundener Klang oder Geräusch: etwa 0,1 Pa = 74 dB (SPL) Häufig irritiert in Büchern das gemeinte Klein-p des Schalldrucks (pressure) geschrieben als Groß-P, das jedoch der Schallleistung (power) vorbehalten ist. |
| Wie nimmt der Schallpegel mit der Schallquellenentfernung ab? Dämpfung des Schallpegels mit dem Schallquellenabstand http://www.sengpielaudio.com/Rechner-entfernung.htm |
| Die Intensität I ist als Leistung pro Flächeneinheit definiert. Die Oberfläche der Kugel ist A = 4 π r2, so dass der Schallleistungspegel Pak, der durch jeden Quadratmeter Oberfläche geht I = Pak / A = Pak / 4 π r2 ist. Man sieht also, dass für eine gleichförmig abstrahlende Schallquelle, die Intensität umgekehrt proportional zum Quadrat der Entfernung r von der Quelle abnimmt: I2 / r12 = I1 / r22. Da aber die Intensität proportional zum Quadrat des Schalldrucks ist, können wir schreiben: p2 / p1 = r1 / r2. Hieraus ist zu erkennen, dass der Schalldruck umgekehrt proportional zum Abstand r von der Quelle abnimmt. Wird der Abstand verdoppelt, so nimmt der Schalldruck um den Faktor 2und die Schallintensität um den Faktor 4 ab. Mit anderen Worten, der Schallpegel verringert sich um (−)6 dB. |
|
Häufig verwirrt es und wird verwechselt, dass der Schalldruck p als Schallfeldgröße mit 1/r mit der Entfernung abnimmt aber die Schallintensität I als Schallenergiegröße jedoch mit 1/r2. I ist proportional p2. Schallfeldgrößen: Schalldruck, Schallschnelle, Schallauslenkung. Hierzu sind proportional die elektrische Spannung, der elektrische Strom und der elektrische Widerstand. Schallenergiegrößen: Schallintensität, Schallenergie, Schallenergiedichte, Schallleistung. Hierzu ist die elektrische Leistung proportional. Intensität bezeichnet umgangssprachlich die Weise, mit der etwas betrieben wird: intensiv, gedrängt, konzentriert. Intensität ist aber speziell in der Physik und in der Akustik ein wichtiger Fachausdruck allein für die Energie. Das Wort Intensität wird recht häufig unrichtig für Stärke, Kraft, Amplitude und Pegel verwendet. Darum sollte der Ausdruck Intensität auch nur genommen werden, wenn wirklich die (Strahlungs-) Energie gemeint ist. In der Tonaufnahmetechnik mit Mikrofonen ist so gut wie immer die Stärke, die Kraft, die Amplitude oder der Pegel gemeint und wirklich nur als seltene Ausnahme einmal die Schallintensität (Energie). Selbst die "Intensitäts"-Stereofonie arbeitet nicht mit den Intensitäten, sondern mit den linearen Schalldruckunterschieden, auch Schalldruckdifferenzen genannt. Was bewegt denn die Mikrofonmembranen und die Trommelfelle? Es ist schlicht der Schallwechseldruck und nicht die gedankenlos dahergesagte Schallintensität. Der Schalldruck ist die in Abhängigkeit von der Zeit und dem Ort erfolgende Druckänderung Δ p als Überlagerung zum atmosphärischen Druck. Der Schallwechseldruck "wirkt" auf die Trommelfelle des Gehörorgans und ist somit für die Schallempfindung maßgeblich. |
| Zusammenhang der akustischen Größen (Schallgrößen) Pegel und Bezugswerte der Schallgrößen - Umrechnungen und Formeln Vergleichende Darstellung von Schallgrößen und Schallenergiegrößen |
Schallpegel-Vergleichstabelle
| Änderung des Schallpegels und die dazugehörende Änderung des Faktors bei Lautstärke (Lautheit), Schalldruck (Spannung) und Schallintensität (Leistung) Wieviel dB Pegeländerung ist zweimal, halb oder viermal so laut? Wieviel dB erscheinen doppelt so laut zu sein? Hier sind die unterschiedlichen Faktoren. |
| Pegel- Änderung |
Lautstärke Lautheit |
Spannung Schalldruck |
Schallleistung Schallintensität |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31,6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2,0 = Verdopplung | 3,16 = √10 | 10 |
| +6 dB | 1,52 fach | 2,0 = Verdopplung | 4,0 |
| +3 dB | 1,23 fach | 1,414 fach = √2 | 2,0 = Verdopplung |
| - - - - ±0 dB - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - |
| −3 dB | 0,816 fach | 0,707 fach | 0,5 = Halbierung |
| −6 dB | 0,660 fach | 0,5 = Halbierung | 0,25 |
| −10 dB | 0,5 = Halbierung | 0,316 | 0,1 |
| −20 dB | 0,25 | 0,100 | 0,01 |
| −30 dB | 0,125 | 0,0316 | 0,001 |
| −40 dB | 0,0625 | 0,0100 | 0,0001 |
| Log. Größe | Psychogröße | Feldgröße | Energiegröße |
| dB- Änderung |
Lautstärke- faktor |
Amplituden- faktor |
Leistungs- faktor |
| Merke: Für eine 10 dB Pegeländerung brauchen wir zehnmal mehr Leistung vom Verstärker. Diese Erhöhung des Schallpegels um 10 dB bedeutet eine Erhöhung des Schalldrucks um den Faktor 3,16. Die psycho-akustische Lautstärke bzw. Lautheit ist eine subjektive Empfindungsgröße. |
| Merke: Eine Anhebung des Schallpegels um 6 dB entspricht der Verdopplung des Schalldrucks. Eine Erhöhung des Schallpegels um 3 dB entspricht der Verdopplung der Schallintensität. Eine Anhebung des Schallpegels um 6 dB entspricht der Vervierfachung der Schallintensität. Eine Erhöhung des Lautstärkepegels um 10 dB soll der Empfindung doppelter Lautstärke entsprechen. Die subjektiv empfundene "Lautstärke" bzw. der "Lautstärkepegel" und der Kunstbegriff "Lautheit" ist als Empfindungsgröße des menschlichen Hörempfindens nicht mit der objektiven Messgröße Schalldruck in einen Topf zu werfen. |
| Merke - Der Schalldruck als Schallfeldgröße ist nicht das Gleiche, wie die Schallintensität als Schallenergiegröße. |
Zusammenhang zwischen Lautstärke und Lautheit - sone und phon
Häufig vorkommende falsche Behauptungen mit Schallgrößen
im Zusammenhang mit dem Abstand von der Schallquelle.
Der Schalldruck nimmt von einer Punktschallquellemit 1/r nach dem Abstandsgesetz ab.
Falsche Abnahme vom Schalldruck mit der Entfernung zur Schallquelle − ohne Quadrat! p ~ 1 / r
| Richtige Version | Falsche Formulierung |
| Der Schalldruck (Amplitude) nimmt bei zuneh- mender Entfernung von der Schallquelle mit 1/r ab. Das ist das reziproke Abstandsgesetz 1/r. |
Der Schalldruck (Amplitude) nimmt bei zuneh- mender Entfernung umgekehrt proportional mit dem Abstand-Quadrat, also mit 1/r2 ab. Sehr falsch |
| Der Schalldruckpegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/2 (50 %) des Schalldruck-Anfangswerts. |
Der Schalldruckpegel nimmt bei zunehmender Entfernung von der Schallquelle mit (−)3 dB je Abstandsverdopplung ab. falsch |
| Die Schallintensität (Energie) nimmt bei zunehmender Entfernung von der Quelle mit 1/r2 ab. Das ist das reziproke Quadratgesetz 1/r2. |
Die Schallintensität (Energie) nimmt bei zuneh- mender Entfernung von der Schallquelle umgekehrt proportional mit dem Abstand 1/r ab. falsch |
| Der Schallintensitätspegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/4 (25 %) des Intensitäts-Anfangswerts. |
Der Schallintensitätspegel nimmt bei zunehmender Entfernung von der Schallquelle mit (−)3 dB je Abstandsverdopplung ab. falsch |
Schalldruck ist nicht Schallintensität
| Weder die Schallleistung, noch der Schallleistungspegel nimmt bei Verdopplung des Abstands um einen Wert bzw. um irgendwelche dBs ab. Weshalb ist das so? Der Schallleistungspegel quantifiziert die gesamte von einem Objekt als Schall abgestrahlte Energie. Anders als der Schalldruck ist die Schallleistung unabhängig von der Entfernung zum Objekt, dem umgebenden Raum und anderen Einflüssen. |
| Unterscheide: Schalldruck p ist eine "Schallfeldgröße" und Schallintensität I ist eine "Schallenergiegröße". Selten wird dieses in der Lehre scharf genug getrennt und bisweilen sogar unrichtig gleichgesetzt. Aber I ~ p2. |
| Frage: Wie geht denn die Abnahme der Schallleistung mit der Entfernung?" Antwort:" April - April. Die Schalleistung Pak nimmt nicht mit der Entfernung von der Schallquelle ab." Der Schallleistungspegel bzw. die Schallleistung ist fest an die Schallquelle gebunden. Die Schallleistung ist von der Entfernung wirklich unabhängig. Schalldruckpegel und Schallintensiätspegel verringern gleichermaßen mit der Entfernung von der Schallquelle ihren Dezibel-Wert. Jedoch hat die Schallleistung bzw. der Schallleistungspegel nichts (!) mit der Entfernung von der Schallquelle zu tun. Gedankenhilfe: Eine 100-Watt-Glühlampe hat in 1 m und in 10 m Entfernung wirklich immer die gleichen 100 Watt, die von der Lampe ständig abgestrahlt (emittiert) wird. Diese Watt ändern sich nicht mit der Entfernung. Eine häufige Frage: "Ist die Schallleistung entfernungsabhängig oder abstandsabhängig?" Die klare Antwort ist: "Nein, weder noch." |
Schalldruck und Schallpegel unter Wasser
| Einfach den Wert links oder rechts eingeben. Rechner arbeitet in beiden Richtungen des ↔ Zeichens. |
| Umrechnung der dB zwischen Luft und Wasser |
| Der Bezugspegel von 0 dB ≡ 1 µPa Druck wurde 1970 von der USA-Marine für Schall in Wasser (Wasserschall) festgelegt. Der Schalldruckpegel von 0 dB in Luft oder Gasen (Luftschall) entspricht einem Schalldruckpegel von 26 dB in Wasser. Für eine identische Quellen-Intensität in Wasser und in Luft, muss der Schalldruck im Wasser etwa 1200 mal größer sein als in Luft. Weiterhin werden Luftschalldruckpegel oft als frequenzbewertete Schalldruckpegel angegeben, um den Frequenzgang des menschlichen Gehörs zu berücksichtigen. Für die Bewertung des Einflusses von Schall in Flüssigkeiten (Wasserschall) auf Meerestiere ist das jedoch kein sinnvoller Bezugsmaßstab. Die schwierige Vergleichbarkeit von Schallpegelangaben für Luftschall und Wasserschall sorgt bei der Diskussion über die Schädlichkeit von Sonaren und Echoloten und bei Geräuschen von Meerestieren immer für ziemliche Verwirrung. Als wichtigste Messgröße für den Wasserschall wird wie beim Luftschall der "Schalldruckpegel" verwendet. Obwohl formal die gleichen Methoden verwendet werden, sind Wasserschall- und Luftschallpegel nur schwer vergleichbar und führen bei Laien immer wieder zu schwerwiegenden Missverständnissen. Pegel sind logarithmische Größen und nur sinnvoll zu interpretieren, wenn die jeweils verwendeten Bezugswerte beachtet werden. Als Bezugswert für den Schalldruckpegel wird beim Luftschall 20 µPa gewählt, beim Wasserschall dagegen 1 µPa. Der Bezugswert beim Luftschall wurde in Anlehnung an die menschliche Hörschwelle gewählt und entspricht bei Ausbreitung einer ebenen Welle im Medium Luft einem Schalldruck von etwa 2 · 10−5 Pascal (20 µPa). Dieser Referenzschalldruck entspricht einer Schall-Intensität von etwa 10−12 W/m². Bekanntlich ist Wasser wesentlich härter als Luft, so dass bei gleicher Intensität die akustisch relevante Partikelgeschwindigkeit wesentlich kleiner, dafür aber der Schalldruck größer ist. Aus diesem Grund ist ein Vergleich der Schalldrücke ohnehin wenig aussagekräftig. Wenn man schon vergleichen will, sollte man eher die Energieflussdichte (Intensität) heranziehen. Weil messtechnisch der Schalldruck besser zugänglich ist, zieht man ihn trotzdem vor. Der dabei verwendete Referenzdruck von 1 µPa entspricht einer Schall-Intensität von etwa 0,65 · 10−18 W/m². Die Beziehungen zwischen Schalldruck und Schall- Intensität sind aber auch einerseits vom Luftdruck, andererseits von Temperatur und Salzgehalt des Wassers abhängig. Näherungsweise unterscheiden sich gleiche Pegelangaben für Luft und Wasser bei ihrem jeweiligen Referenzdruck in ihrem Pegel um etwa 62 dB. Für eine - ohnehin fragliche - Vergleichbarkeit der Pegel sind also vom Wasserschall etwa 62 dB abzuziehen. Der große Unterschied des Pegels von Schall in Luft und die Pegelangabe des Schalls unter Wasser in Dezibel (dB) wird selten erkannt und deutlich erklärt. |
Wie ist Schall in Wasser unterschiedlich
im Vergleich zu Schall in der Luft?
| Ein Vergleich von Schallpegeln in Luft gegenüber Schallpegeln in Wasser muss sehr sorgfältig durchgeführt werden. Luft und Wasser haben zueinander einen unterschiedlichen Referenzschalldruck von 26 dB. Aufgrund der Differenz der Impedanz (die Steifigkeit und Dichte des Mediums) zwischen Luft und Wasser, ist ungefähr ein 3.500 Mal größerer Leistungspegel (36 dB) in der Luft erforderlich, um einen entsprechenden Druckpegel in Wasser zu erzeugen. Durch Kombination beider Werte wird ein Korrekturfaktor von 26 dB + 36 dB = 62 dB zwischen den beiden Skalen erforderlich. Daher muss 62 dB von einem Geräuschpegel in Wasser abgezogen werden, um eine äquivalente akustische Intensität in Luft zu erzeugen. Es ist irreführend, die Dezibelwerte der Geräusche des Unterwasser-Sound mit den Dezibel- Werten von in der Luft gehörten Geräuschen zu vergleichen. |
| Mikrofone, die unter Wasser angewendet werden heißen Hydrophone. Man kann diese bei DPA bekommen. Übliche Mikrofone müssen dabei unbedingt vor Wasser geschützt werden. Einfallsreiche Tontechniker ziehen bei Außenaufnahmen im Regen oder unter Wasser im Schwimmbad praktischer Weise ein Kondom über ein handelsübliches Kleinmikrofon. Das ist kein Witz. Die schlaffe Latex-Haut dichtet die Mikrofonkapsel wasserdicht ab und allein die reine Druckänderung (Skalar) wird übertragen - jedoch ist dieser Trick nur bei reinen Druckempfängern anwendbar, also bei Mikrofonen mit Charakteristik Kugel. Bei Druckgradientenempfängern, wie z. B. bei Mikrofonen mit Richtcharakteristik Niere, funktioniert dieses mit dem "Verhüterli" nicht, denn die Druckgradientenbewegung (Vektor- Druckunterschied vor und hinter der Membran) ist heftig gestört. Bei allen Tipps in "YouTube" zu Methoden ein Mikrofon wasserdicht zu machen, wird immer vergessen zu erklären, dass es eben nicht ordentlich bei "Nierenmikrofonen" und anderen Druckgradientenempfängern funktionieren kann. Man weiß es halt nicht besser; siehe: YouTube: Waterproofing a microphone with a condom Der Rat, ein Soundfieldmikrofon für eine Surround-Sound-Aufnahme unter Wasser mit einem Kondom zu verwenden, musste als unsinnig erkannt werden, denn Druckgradientenempfänger verlieren dadurch völlig ihre Wirkung. |
| Merke: Nur Mikrofone mit Kugelcharakteristik funktionieren mit "Verhüterli" unter Wasser. |
| Die internationalen Druckeinheiten Mehr Umrechnung von Druckeinheiten Umrechnung der Druckeinheiten |
| Frage: Wie groß ist der Standard-Abstand, um den Schalldruckpegel von einer Schallquelle zu messen? Es gibt keinen genormten Abstand. Er hängt von der Größe der Schallquelle und dem Schallpegel ab. |
Bewerteter Schall wird nicht in phon, sondern in dB(A) angegeben.
| Umwandlung von Schall-Einheiten Schallintensität: Bezugsschallintensität I0 = 10−12 W/m2 (Hörschwelle) Bezugsschallintensitätspegel LI0 = 0 dB-SIL (Hörschwellen-Pegel) Berechnen der Schallintensität I bei Eingabe des Schallintensitätspegels LI: I = I0·10(L/10) in W/m2 = 10−12·10^(LI / 10) in W/m2. Berechnen des Schallintensitätspegels LI in dB bei Eingabe von Schallintensität I in W/m2: LI = 10·log (I / I0) in dB = 10·log (I / 10−12) in dB. Schalldruckpegel Bezugsschalldruck p0 = 20 µPa = 2·10−5 Pa (Hörschwelle) Bezugsschalldruck Lp0 = 0 dB-SPL (Hörschwellen-Pegel) Berechnen des Schalldrucks p bei Eingabe des Schalldruckpegels Lp: p = p0·10^(Lp / 20) in Pa (= N/m2) = 2·10−5·10^(Lp / 20) in Pa (N/m2). Berechnen des Schalldruckpegels Lp in dB bei Eingabe des Schalldrucks p in Pa: Lp = 20·log (p / p0) in dB = 20·log (p / 2×10−5) in dB. Wie addiert man zwei Schallintensitätspegel LI1 = 50 dB und LI2 = 65 dB? Raus aus dem Pegel und zurück zum Zahlenverhältnis (Energiegröße). (Die Bezugs-Schallintensität wird hier nicht benötigt.) I1 = 10^(LI1/10) = 10^(50/10) = 100000. I2 = 10^(LI2/10) = 10^(65/10) = 3162277. Beide Werte werden addiert. Man erhält I = I1 + I2 = 3262277. Nun zurück zum Pegel: LI = 10 · log (3262277) = 65,13 dB. Für große Unterschiede über 10 dB, nimmt man nur den höchsten Wert. Wie addiert man zwei Schalldruckpegel Lp1 = 50 dB und Lp1 = 65 dB? Raus aus dem Pegel und zurück zum Zahlenverhältnis (Feldgröße). (Der Bezugs-Schalldruck wird hier nicht benötigt.) p1 = 10^(Lp1/20) = 10^(50/20) = 316. p2 = 10^(Lp2/20) = 10^(65/20) = 1778. Pythagoras: p = √ (p12+p22) = √ (3162 + 17782) = 1806. Nun zurück zum Pegel: Lp = 20 · log (1806) = 65,13 dB. Für große Unterschiede über 10 dB, nimmt man nur den höchsten Wert. |
| Was ist der größte Schalldruck? Wie viele Dezibel hat das lauteste Geräusch? |
| Eine typische falsche Aussage: "Lärmpegel können nicht lauter als 194 dB sein." Liegt das Ende bei 194 dB? Öfter wird diese Wahrnehmungsschwelle als physikalische Grenze diskutiert. Schall ist nichts weiter als eine Störung des Luftdrucks und 194 dB ist theoretisch die gleiche Größe wie der Luftdruck selbst. Der Schall muss dabei verzerrt sein. Ein lauterer Lärm ist schon möglich, jedoch stark verzerrt. Das ist eben Chaos. Dieser hohe Schalldruck zerstört alle Mess-Mikrofone und auch Menschen, beispielsweise in der Nähe des Zentrums einer nuklearen Explosion. Kein Gehörschutz (Ohrenschützer oder Ohrstöpsel) kann uns dann noch helfen. |
| Information über den Hörpegel - Hearing Level (HL) Sinustöne werden als audiometrische Schwellen in dB HL ausgedrückt. |
| Frequenz | dB SPL | dB HL |
| 250 Hz | +15.0 | 0.0 |
| 500 Hz | +9.0 | 0.0 |
| 1000 Hz | +3.0 | 0.0 |
| 2000 Hz | −3.0 | 0.0 |
| 4000 Hz | −4.0 | 0.0 |
| 8000 Hz | +13.0 | 0.0 |
| zurück |
Suchmaschine |
Startseite |