

| English version |
| Alle diese Pegel haben die gleiche Maßeinheit: das Dezibel (dB). Allgemein wird der Begriff
"Schallpegel" für diese Pegelgrößen verwendet. Bei der Kennimpedanz der Luft wird üblicherweise der runde Wert Z = 400 N·s/m³ (Pa·s/m) eingesetzt. Dann stimmt der "Schallpegel" als Dezibel-Wert, also der Schalldruckpegel Lp und der Intensitätspegel LI genau überein. Die Schallleistung ist die pro Sekunde von der Schallquelle ständig abgegebene Schallenergie. Eine Schallquelle hat eine konstante Schallleistung, die sich nicht ändert, wenn sie in eine andere Raumumgebung abstrahlt (emittiert). Die Schallleistung ist eine theoretische Größe, die nicht messbar ist. Sie wird berechnet und in Watt angegeben und als Schallleistungspegel LW in dB. Eine Schallquelle erzeugt Schallleistung und diese erzeugt Schalldruckschwankungen in der Luft. Die Schallleistung ist dafür die raum- und entfernungsunabhängige Ursache, während der Schalldruck die entfernungsabhängige Wirkung ist. |
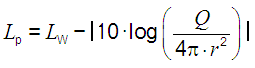 |
| In r = 1 m Entfernung ist der Schalldruckpegel (SPL) einer Punktschallquelle um 11 dB geringer als ihr Schallleistungspegel (SWL), wenn Q = 1, also die volle Kugel-Abstrahlung gegeben ist. |
| Für Q = 1 (volle Kugel-Abstrahlung) ist der Schallleistungspegel gleich groß wie der Schalldruckpegel oder der Schallintensitätspegel, wenn der Abstand von der Schallquelle r = 0.2821 m = √ (1/(4·π)) m beträgt. |
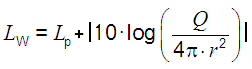 |
| Die Schallleistung bzw. der Schallleistungspegel haben absolut nichts mit der Entfernung zu tun. Gedankenhilfe: Eine 100 Watt-Glühlampe emittiert ständig die gleiche Leistung. Das ist so - egal ob in 1 m, in 10 m oder selbst in 100 m Abstand. Diese emittierten Watt ändern sich nicht mit der Entfernung (Abstand, Distanz). Die Schallleistung ist die entfernungsunabhängige Ursache während der Schalldruck die entfernungsabhängige Wirkung ist. |
 |
 |
| Häufig wird behauptet, dass Schalldruckpegel = SPL, Schallintensitätspegel = SIL und Schallleistungspegel = SWL nicht vergleichbar sind. SPL wird in Pascal oder N / m2 gemessen; Schallintensität ist Energie und wird in W / m2 gemessen und Schallleistungspegel wird in Watt gemessen. Kaum bekannt ist, dass der Schallleistungspegel (ohne (!) Abstandsmaß r) der gleiche ist wie der Schalldruckpegel und der Intensitätspegel bei einer Entfernungvon der Schallquelle bei Rundumabstrahlung Q = 1 von r = 0,2821 m. 1 Watt Schalleistungspegel = 120 dB Schallintensität bei r = 0,2821 m: Pak = 1 Watt / (4π · r2) = 1 Watt, d. h. (4π · r2) = 1 und r = √(1/4π). 10 · log (1/10−12) = 120 dB Schalldruckpegel SPL bei 0,2821 m = SWL − (20 · log (r) − 11) = 120 − (20 · log (0,2821) − 11) = 120 dB Wie können diese also nicht vergleichbar sein? Der Schallintensitätspegel und der Schalldruckpegel in einem Abstand von 1 Meter von der Quelle im Freifeld ist 11 dB weniger als der Schallleistungspegel der Quelle. SIL = SPL = SWL − 11 dB or LI = Lp = LW − 11 dB. Die akustische Impedanz von Luft ist Z0 = 400 Pa×s/m. |
| Unterscheide: Schalldruck p ist eine "Schallfeldgröße" und Schallintensität I ist eine "Schallenergiegröße". Selten wird dieses in der Lehre scharf genug getrennt und bisweilen sogar unrichtig gleichgesetzt. Aber I ~ p2. |
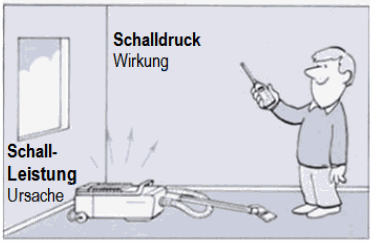
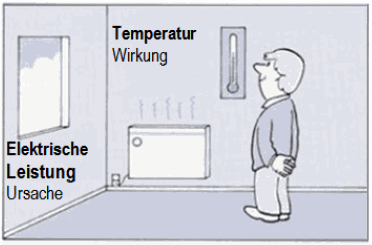
| Wichtig: Der Schalldruckpegel ist nicht mit Schallleistungspegel zu verwechseln! Die dB-Werte beim Schalldruckpegel sind immer an die Entfernung zur Schallquelle gebunden; dagegen haben die dB-Werte beim Schallleistungspegel keine Beziehung zum Abstand von der Schallquelle. Frage: Wie geht denn die Abnahme der Schallleistung mit der Entfernung?" Antwort:" April - April. Die Schalleistung Pak nimmt nicht mit der Entfernung von der Schallquelle ab." Der Schallleistungspegel bzw. die Schallleistung ist fest an die Schallquelle gebunden. Die Schallleistung ist von der Entfernung wirklich unabhängig. Schalldruckpegel und Schallintensiätspegel verringern jedoch gleichermaßen mit der Entfernung von der Schallquelle ihren Dezibel-Wert. Jedoch hat die Schallleistung bzw. der Schallleistungspegel nichts (!) mit der Entfernung von der Schallquelle zu tun. Gedankenhilfe: Eine 100-Watt-Glühlampe hat in 1 m und in 10 m Entfernung wirklich immer die gleichen 100 Watt, die von der Lampe ständig abgestrahlt (emittiert) wird. Diese Watt ändern sich nicht mit der Entfernung. Eine häufige Frage: "Ist die Schallleistung entfernungsabhängig oder abstandsabhängig?" Die klare Antwort ist: "Nein, weder noch." |
 |
 |
| Schallleistung und Schallleistungspegel |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Die Schallleistung ist weder raumabhängig noch entfernungsabhängig. |
Direkte Umrechnung von Schalldruck in Schallintensität und zurück
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Während der Schalldruckpegel in Luft mit dem Schallintensitätspegel übereinstimmt, wenn als Bezugs-Schallkennimpedanz Z0 = 400 N·s/m³ gewählt wird, ist das beim entfernungsunabhängigen Schallleistungspegel nicht der Fall. |
Gleicher Schallpegel bei Abstand (Entfernung) r = √(Q / 4π)
| Geometrie |
Richtungs- faktor Q |
Gleicher Schallpegel bei Entfernung r |
r dB |
| Keine Fläche in der Nähe der Schallquelle; strahlt akustische Energie in alle Richtungen; Vollkugel |
1 | √(1/4π) = 0.2821 m | 11 |
| Schallquelle dicht an einer ebenen Fläche; strahlt akustische Energie als die Hälfte einer Kugel |
2 | √(1/2π) = 0.3989 m | 8 |
| Zwei benachbarte ebene Flächen senkrecht zu einander, strahlt akustische Energie als ein Viertel einer Kugel |
4 | √(1/π) = 0.5642 m | 5 |
| In einer Ecke; strahlt akustische Energie als ein Achtel einer Kugel |
8 | √(2/π) = 0.7979 m | 2 |
 |
 |
 |
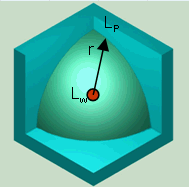 |
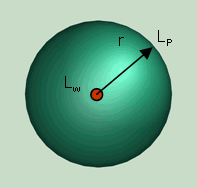
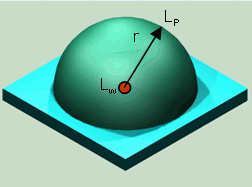
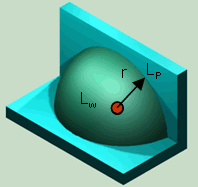
| Vollkugel Q = 1 Halbkugel Q = 2 Viertelkugel Q = 4 Achtelkugel Q = 8 |
| Für die praktisch vorkommenden Raumwinkel gelten die folgenden Beziehungen zwischen dem Schallleistungs- und dem Schalldruckpegel Für Q = 1 ist LW = Lp + [20 log10 (r)] + 11 dB (voll) Für Q = 2 ist LW = Lp + [20 log10 (r)] + 8 dB (halb) Für Q = 4 ist LW = Lp + [20 log10 (r)] + 5 dB (viertel) Für Q = 8 ist LW = Lp + [20 log10 (r)] + 2 dB (achtel) Lp = mittlerer Schalldruckpegel auf der Hüllfläche bzw. für den häufigsten Fall der Halbkugelabstrahlung r = 1 m: LW = Lp + 8 dB |
| Kugelförmige Freifeld Schallausbreitung, Q = 1 |
|
Der Schalldruck in einem kugelförmigen Abstand von einer Quelle mit einem bekannten Schallleistungspegel kann ausgedrückt werden als: 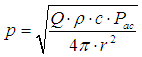 (1) (1)wobei p = Schalldruck in Pa = N/m2 ρ = Luftdichte in kg/m3: 1,2041 kg/m3 bei 20°C c = Schallgeschwindigkeit in m/s: 343,42 m/s bei 20°C Pac = Schallleistung in W π = 3.14159 r = Abstand von der Schallquelle in m Q = Richtungsfaktor (Kugel = 1, Halbkugel = 2) Richtungsfaktor = directivity index - directivity factor - directivity coefficient |
| Für eine kugelförmige Schallausbreitung (Q = 1) in einem Abstand von r = √(1/4π) = 0.2821 m ist der Dezibel-Wert des Schalldruckpegels gleich dem des Schallleistungspegels. |
| Halbkugelförmige Freifeld Schallausbreitung, Q = 2 |
| Der Richtungsfaktor Q hängt von mehreren Parametern ab − dem Ort
und der Richtung der Schallquelle, dem umgebenden Raum usw. Der Schalldruckpegel Lp kann logarithmisch ausgedrückt werden: Lp = 20 · log (p/p0) = 20 · log ((Q · ρ · c · Pac/(4π · r2))1/2/p0) = 20 · log (1/r (Q · ρ · c · Pac/(4π))1/2/p0) (2) wobei Lp = Schalldruckpegel in dB p0 = 2 · 10−5 - Bezugs-Schalldruck in Pa Merke: Für jede Verdopplung des Abstands von der Schallquelle wird der Schalldruckpegel Lp um 6 dB geringer. |
| Für eine halbkugelförmige Schallausbreitung (Q = 2) in einem Abstand von r = √(1/2π) = 0.3989 m ist der Dezibel-Wert des Schalldruckpegels gleich dem des Schallleistungspegels. |
| Bei punktförmigen Schallquellen ist eine kugelförmige Fläche A anzusetzen. Je nach Anordnung im Raum sind folgende Kugelabschnitte zu berücksichtigen: Vollkugel - Schallquelle frei im Raum, Q = 1 Halbkugel - Schallquelle auf dem Boden, Q = 2 Viertelkugel - Schallquelle an der Wand, Q = 4 Achtelkugel - Schallquelle in der Ecke, Q = 8 Q = Richtungsfaktor und Fläche A = (4π · r2) / Q |
| Schallintensität I = Schallleistung Pak / Fläche A Schallleistung Pak = I · A = I · 4π · r2. |
| Sound Pressure Level Calculator |
| Consider a source of sound and imagine a sphere with radius r, centered on the source. The sound source outputs a total power P, continuously. The sound intensity I is the same everywhere on this surface of a thought sphere, by definition. The intensity I is defined as the power P per unit area A. The surface area of the sphere is A = 4π · r2, so the sound intensity passing through each square meter of surface is, by definition: I = P / 4π · r2. We see that sound intensity is inversely proportional to the square of the distance away from the source (1/r2): I2 / I1 = r12 / r22. But sound intensity is proportional to the square of the sound pressure, I ~ p2, so we can write: p2 / p 1 = r1 / r2. The sound pressure p changes with 1 / r of the distance. So, if we double the distance, we reduce the sound pressure by a ratio of 2 and the sound intensity by a ratio of 4: In other words, we reduce the sound level by 6 dB. If we increase r by a ratio of 10, we decrease the level by 20 dB. |
|
Unterscheide Schalldruck und Schallleistung Störquelle - Musikinstrument? Schalldruckpegel ist nicht Schallleistungspegel Der Zusammenhang der Schallgrößen - Die Pegel und die Bezugswerte |
| Wenn eine Punktschallquelle gleichmäßig den Schall in alle Richtungen in
einem freien Feld emittiert, dann wird sich die Energie über die
Oberfläche einer Kugel mit zunehmendem Radius ausbreiten. Die Oberfläche der vollen Kugel ist 4π · r². Richtungsfaktor Q = 1. Die gleiche Menge an Energie breitet sich über eine immer größer werdende Fläche aus. Daher wird die Intensität abnehmen. Die Schallquelle emittiert ständig die Schallleistung, die dort verbleibt. Die Schallleistung nimmt nicht mit der Entfernung von der Schallquelle ab. |
| Konvertieren von Schallleistungspegel in Schalldruckpegel |
| Eine Lärmquelle emittiert ständig Leistung, die als Schallleistungspegel
gemessen wird. Es ist ein Merkmal der Schallquelle allein und ist unabhängig von der Entfernung. Der Schalldruckpegel der Quelle ist der Schallpegel der Quelle, der aber mit einem Abstand von ihr verursacht wird. Die Höhe der Schalldrucks ist daher vom Abstand abhängig. Die Formel für die Umrechnung Schallleistungspegel in Schalldruckpegel ist: Lp = LI = LW − 10 · log (Q / 4π · r²) in dB Für Q = 1 ist LW = Lp + [20 · log10(r)] + 11 dB Für Q = 2 ist LW = Lp + [20 · log10(r)] + 8 dB, wobei Schalldruckpegel = SPL oder Lp in dB, Schallleistungspegel SWL, LPak oder LW in dB, Entfernung des Messpunktes von der Schallquelle = r. |
W. T. W. CORY: "Relationship between Sound pressure and Sound Power Levels"
| Leistung ist wie alle Energiegrößen überwiegend eine berechnete Größe. |
| "Schallleistung" und "Schalldruck" sind zwei unterschiedliche Schallgrößen, die
häufig verwechseltwerden. Sie haben eine Ursache- und Wirkungs-Beziehung. Schallleistung ist die akustische Energie, die von der Schallquelle ausgesendet wird und ein absoluter Wert ist. Schallleistung wird nicht durch die Umgebung beeinflusst. Schallleistungspegel ist mit der Schallquelle verbunden und ist unabhängig von der Entfernung. Schallleistungspegel werden in Dezibel angegeben: Lw = 10 · log (P / P0), wobei: Die Bezugsleistung ist P0 = 10−12Watt (W) , das ist die niedrigste Schallleistung die Personen mit ausgezeichnetem Gehör wahrnehmen können. Schallleistung wird als Gesamtschallleistung die eine Quelle in alle Richtungen emittiert in Watt (Joule pro Sekunde) gemessen. Da Schallmessinstrumente auf Schalldruckpegel gemessen in "Dezibel" reagieren, sind sie allgemein mit dem Schalldruckpegel (SPL) verbunden. Schalldruckpegel in Dezibel zu quantifizieren, die Intensität der Schallquellen gegeben. Schalldruckpegel variieren wesentlichen mit Abstand von der Quelle , und auch infolge der dazwischen Hindernisse und Barrieren, Luftabsorption , Wind und anderen Faktoren verringern. Schalldruckpegel wird in Dezibel angegeben. Schalldruckpegel (SPL) ist: Lp = 20 · log (p / p0), wobei der Bezugsschalldruck p0 = 2 · 10−5 Pa = 20 µPa ist. Schalldruck ist eine Druckstörung in der Luft , deren Stärke nicht nur durch die Quelle beeinflusst wird, sondern auch von der Umgebung und der Entfernung von der Quelle zum Empfänger. Schalldruck ist, was unsere Ohren hören und was Schalldruckpegelmesser (SPL Meter) eben messen. |
| zurück |
Suchmaschine |
Startseite |