

| English version |
| Das Dezibel ist eine Hilfsmaßeinheit, die das Verhältnis zweier Feldgrößen (Spannung) oder Energiegrößen
(Leistung) angibt. Bei der Verwendung einer fest gewählten Bezugsgröße, kann es auch als Pseudo-Einheit
(Pegel) verwendet werden. Das Dezibel (dB) ist ein Mittel zum Ausdruck der Verstärkung (Gain) eines
aktiven Bauteils (wie z. B. einen Verstärker) oder die Dämpfung eines passiven Bauteils (wie z. B. ein
Spannungsteiler oder die Länge eines Kabels). Es ist einfach das Verhältnis von Spannung am Ausgang zur Spannung am Eingang, das
in logarithmischer Form ausgedrückt wird. Der Fachausdruck für das Größenverhältnis von Ausgang zu Eingang bei einem Verstärker ist die Verstärkung (engl. gain). Als Verhältnis von gleichen Einheiten, wie Spannung am Ausgang zu Spannung am Eingang, ist die Verstärkung natürlich eine einheitenlose Messung. Die Verstärkung v wird linear als Verstärkungsfaktor oder logarithmisch als Verstärkungsmaß oder als Verstärkungsgrad in Dezibel (dB) ausgedrückt: Verstärkung v = 20 · log (U2 / U1) in dB U1 = Eingangsspannung als Bezugswert und U2 = Ausgangsspannung |
| In der Audiotechnik, ist Gain = Verstärkungsfaktor ein Maß für die Fähigkeit des
Verstärkers, die Amplitude (oder recht selten die Leistung) eines Signals vom Eingang
zum Ausgang zu erhöhen. Die Verstärkung wird gewöhnlich als das mittlere Verhältnis des
Signalausgangs eines Systems zum Signaleingang des gleichen Systems definiert. Die Verstärkung kann auch mit einer logarithmischen Skala definiert werden, in Bezug auf den dekadischen Logarithmus und dem gleichen Verhältnis ("dB Gain"). Ein "Gain" größer als Eins (entsprechend 0 dB) heißt Verstärkung und ist die bestimmende Eigenschaft einer aktiven Schaltung, während eine passive Schaltung ein "Gain" von weniger als Eins ergibt, was Dämpfung (Loss) genannt wird. Berechnen der Verstärkung (gain) und der Dämpfung (loss) als Pegel in Dezibel Die Dezibel-Verstärkung sollte nie beim dB ein Anhängsel haben. |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Bei der Feldgröße x ist immer der Effektivwert (eff) gemeint - jedoch nicht bei der Energiegröße y.
Energiegröße y ist Feldgröße x (Amplitude eff) zum Quadrat: y ~ x2.
| Elektrische Größen | Akustische Größen |
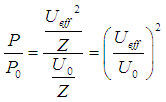 |
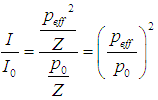 |
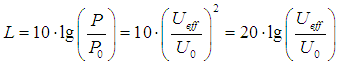 |
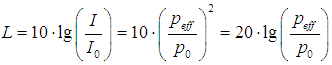 |
| Verhältnisse und Pegel in der Elektrotechnik und der Akustik | |
| Spannungsverstärkung (voltage gain) |
| Leistungsverstärkung (power gain, energy gain) |
Spannungsverhältnis  = Verstärkungsfaktor (Spannung) = Verstärkungsfaktor (Spannung) |
Leistungsverhältnis 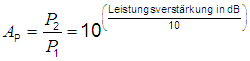 = Verstärkungsfaktor (Leistung) = Verstärkungsfaktor (Leistung) |

| U2 > U1 heißt Verstärkung. Der dB-Wert ist positiv (+) U2 < U1 heißt Dämpfung. Der dB-Wert ist negativ (−). U2 / U1 heißt Verhältnis-Faktor. Das Verstärkungsmaß oder Dämpfungsmaß in dB ist: L = 20 · log (Spannungsverhältnis U2 / U1) U1 ist der Bezugswert des Eingangs. |
| Gain/loss als Verhältnis (ratio out/in) |
Gain/loss als Faktor (factor) |
Gain/loss in dB als Feldgröße (Spannung) |
Gain/loss in dB als Energiegröße (Leistung) |
| 10000:1 | 10000 | +80,00 dB | +40,00 dB |
| 1000:1 | 1000 | +60,00 dB | +30,00 dB |
| 100:1 | 100 | +40,00 dB | +20,00 dB |
| 10:1 | 10 | +20,00 dB | +10,00 dB |
| 5:1 | 5 | +13,98 dB | +6,99 dB |
| 4:1 | 4 | +12,04 dB | +6,02 dB ● |
| 2:1 | 2 | +6,02 dB ● | +3,01 dB |
| 1:1 | 1 | 0,00 dB | 0,00 dB |
| 1:2 | 0,5 | −6,02 dB ● | −3,01 dB |
| 1:4 | 0,25 | −12,04 dB | −6,02 dB ● |
| 1:5 | 0,2 | −13,98 dB | −6,99 dB |
| 1:10 | 0,1 | −20,00 dB | −10,00 dB |
| 1:100 | 0,01 | −40,00 dB | −20,00 dB |
| 1:1000 | 0,001 | −60,00 dB | −30,00 dB |
| 1:10000 | 0,0001 | −80,00 dB | −40,00 dB |
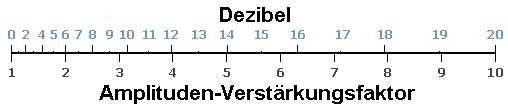
40 dB Spannungs-Gain ist 100 Mal der Spannungsfaktor (Amplitude).
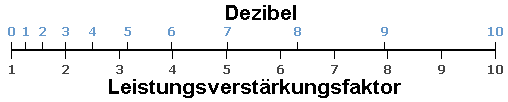
40 dB Leistungs-Gain ist 10000 Mal der Leistungsfaktor (Energie)
Spannungsverstärkung Voltage Gain und
Leistungsverstärkung Power Gain
Was ist Amplitude? − Schall-Amplitude
| Spannungsverstärkung Voltage Gain (Amplitude) |
Leistungsverstärkung Power Gain (Energie) |
|||
| Spannungsverhältnis Faktor U2/U1 |
Spannungsverstärkung GV in dB |
Leistungsverhältnis Faktor P2/P1 |
Leistungsverstärkung GP in dB |
|
| 103 | +60 | 106 | +60 | |
| 102 | +40 | 104 | +40 | |
| 101 | +20 | 102 | +20 | |
| √10 = 3,16 | +10 | 10 | +10 | |
| 2 | +6 | 4 | +6 | |
| √2 = 1,414 | +3 | 2 | +3 | |
| 1 | ±0 | 1 | ±0 | |
| 1/√2 = 0,7071 | −3 | 1/2 = 0,5 | −3 | |
| 1/2 = 0,5 | −6 | 1/4 = 0,25 | −6 | |
| 1/√10 = 0,316 | −10 | 10−1 = 0,1 | −10 | |
| 10−1 = 0,1 | −20 | 10−2 = 0,01 | −20 | |
| 10−2 = 0,01 | −40 | 10−4 = 0,0001 | −40 | |
| 10−3 = 0,001 | −60 | 10−6 = 0,000001 | −60 | |
| V2/V1 = 10(GV in dB/20) | GV = 20·log (V2/V1) | P2/P1 = 10(GP in dB/10) | GP = 10·log (P2/P1) | |
| In der Tontechnik wird der Begriff "power gain = Leistungsverstärkung" nicht verwendet. Lautstärke ist englisch gain, level oder volume. Für Amateure ist "Gain" (engl: "Gewinn, Verstärkung") die Pegelanhebung des "Preamps" mit einem Drehregler (Poti), der für den Verzerrungsgrad des Gitarrensignals im "Amp" zuständig ist. Der Verstärkungsfaktor, engl. gain genannt, ist das Ausmaß, in dem ein analoger Verstärker die Stärke eines Signals verstärkt. Bei einem elektronischen Verstärker ist das Eingangssignal üblicherweise eine Spannung. Gain in dB ist das logarithische Verhältnis zwischen der Eingangs- und der Ausgangsspannung des Vorverstärkers. Typische Werte liegen zwischen 0 und 70 dB. Gain und Loss können als einheitsloses Verhältnis (ratio) oder in der Dezibel- Einheit (dB) angegeben werden. Eine Verstärkung mit dem Faktor 1 - entsprechend 0 dB - wobei sowohl Eingang und Ausgang auf gleicher Spannung steht, wird mit Eins-Verstärkung (unity gain = Verstärkungsfaktor 1) bezeichnet. |
| Der Pegel der Ausgangsleistung ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 50% (Faktor = 0.5) und der Pegel von −6 dB ist entsprechend 25% (= 1/4 = 0,25) der ursprünglichen Leistung. Dieses gilt für die Energiegröße. Der Pegel der Ausgangsspannung ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 70,7% (Faktor = 0,7071), und der Pegel von −6 dB ist entsprechend 50% (= 1/2 = 0,5)der ursprünglichen Spannung. Dieses gilt für die Feldgröße. |
| Akustiker und Schallschützer ("Lärmbekämpfer") brauchen die Schall- intensität und die Schallleistung – jedoch benötigen Tontechniker und Sound-Designer ("Ohrenmenschen") diese Schallenergiegröße kaum. Daher sollte man sich eher um die Schallfeldgröße, den Schallwechseldruck kümmern und um den Pegel (Schalldruckpegel SPL) als Wirkung an den Trommelfellen des Gehörs und an den Membranen der Mikrofone, sowie der entsprechenden Audiospannung bzw. seinem Spannungspegel. |
| Solch eine logarithmische Göße ist gut verwendbar, weil z. B. die Dezibel-Verstärkungswerte von mehreren Verstärkern in einer Reihe einfach addiert werden können, um die Gesamtverstärkung der Verstärkerkette zu erhalten. Die Anzahl der Dezibel ist 20 mal der Logarithmus (zur Basis 10) der Amplitudenverhältnisse als Effektivwert einer Feldgröße oder alternativ 10 mal der Logarithmus (zur Basis 10) des Leistungsverstärkungsfaktors einer Energiegröße. |
 |
 |
| Eine typische Frage: "16 dB sind wieviel Mal?" Antwort: Ist eine Feldgröße, wie Schalldruck oder ist eine Energiegröße, wie Schallintensität gemeint? Deswegen gibt der Rechner zwei Antworten: Der Faktor ist: 6,31 oder der Faktor ist: 39,8; je nachdem, ob eine Feldgröße oder eine Energiegröße gemeint ist. 6,312 (Feldgröße zum Quadrat) = 39,8 (Energiegröße). |
| Fragen: Für einen Verstärker mit einer 100-fachen Spannungsverstärkung, berechne man das Folgende: a) Der Verstärkungspegel (Gain) in dB. b) Der Verstärkungspegel (Gain) bei der Grenzfrequenz in dB. c) Spannungsverstärkung bei der Grenzfrequenz. Antworten: a) Spannungsverstärkung 100 ≡ 40 dB Voltage Gain b) Bei der Grenzfrequenz gibt es 3 dB weniger Gain − also 37 dB. c) Voltage Gain 37 dB ≡ 70,7-fache Spannungsverstärkung. |
| zurück |
Suchmaschine |
Startseite |