

| English version |
| Schall wahrzunehmen bedeutet räumliches Hören. Schall ist entweder nützlich oder nutzlos. Gewünschter Schall ist Information (Nutzschall) und angenehm für uns. Ungewünschter Schall ist Lärm (Störschall) und nervt uns. Oft ist es schwierig zu entscheiden, ob Schall Information oder Lärm ist. |
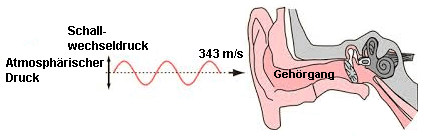
Schallwellen bewegen unsere Trommelfelle.
Aber welche Schallgröße erzeugt denn diese Wirkung?
 |
|
Schalldruck und Schallleistung – Wirkung (Effekt) und Ursache Schallleistung ist zwar die Ursache - aber Schalldruck erzeugt die hörbare Wirkung (Effekt). |
| Schalldruck p in Pa oder N/m Schallintensität I in W/m² Schallkennimpedanz Z = ρ0 · c in N·s/m³ oder Pa·s/m Schallpegel Lp = 20 · log (p / p0) = LI = 10 · log (I / I0) = 10 · log (p² / p0²) in dB Die dB-Skala in dB Bezugswerte (Referenzwerte) p0, I0 |
| Schalldruck Schallwellen sind Druckschwankungen (Schallwechseldruck), Verdichtung (Kompression) und Verdünnung der Moleküle durch ein Medium in dem sich Schallwellen ausbreiten. Die Einheit für den Schalldruck ist Pascal (Pa), entsprechend Newton pro Quadratmeter (N/m²). Der Schalldruck kann mit einem druckempfindlichen Gerät, wie etwa einem Mikrofon (Luft) oder einem Hydrophon (Wasser) gemessen werden. Intensität I und Schalldruck p sind in einer ebenen Welle gegeben durch die Gleichung: I = p² / (ρ0 · c) in Watt/m², ρ0 · c = Z0 als charakteristische akustische Impedanz wobei ρ0 die spezifische Dichte des Mediums ist, durch welche der Schall sich ausbreitet. c ist die Ausbreitungsgeschwindigkeit des Schalls (Schallgeschwindigkeit) im Medium. Die momentane Schallschnelle (Partikelgeschwindigkeit) v in der ebenen Welle kann durch folgende Gleichung auf den Schalldruck p bezogen werden: v = p / (ρ0 · c) in m/s. Die Amplitude der Teilchenauslenkung ξ (xi) (Partikelbewegung) einer Schallwelle ist durch folgende Gleichung auf den Schalldruck und die Frequenz bezogen: ξ = p / (ω · ρ0 · c) in m (RMS), wobei ω = 2π · f die Kreisfrequenz und f die Frequenz der Welle ist. Die obigen Formeln haben bei ebenen und bei sphärischen Wellen ihre Gültigkeit, wenn der Abstand zur Schallquelle mehr als eine Wellenlänge bei der niedrigsten Frequenz beträgt, also im Fernfeld ist. Der Schalldruck, welcher der untersten Grenze des menschlichen Gehörs entspricht ist 20 µPa, entsprechend einer Schallintensität von 10−12 Watt/m² ergibt eine Auslenkung des Trommelfells (Ausschlag), die in der Größenordnung von 10−9 Zentimeter bei einer Frequenz von 1000 Hz liegt. Dieses ist etwa ein Zehntel des Durchmessers eines Wasserstoffmoleküls. Schallintensität Die Schallintensität I einer Schallwelle wird als durchschnittliches Verhältnis des Energieflusses durch eine Flächeneinheit senkrecht zur Wellenausbreitungsrichtung definiert. Die Einheit für die Schallintensität ist Watt pro Quadratmeter (W/m²), was gleichbedeutend auch Joule pro Sekunde pro Quadratmeter (J/s/m²) ist. In einigen Fällen wurde festgestellt, dass die Lautstärke des Schalls durch seine (Schall-)Intensität bestimmt wird. Dieses gilt jedoch nicht für den allgemeinen Fall, denn Lautstärke und Schallintensität sind nicht synonym (bedeutungsgleich). Die Lautheit (Lautstärke) ist immer subjektiv und in allen Fällen ist sie eine Kombination aus empfundener Schallintensität und Frequenz. Schallkennimpedanz (Charakteristische akustische Impedanz) Der Faktor ρ0 · c wird mit Schallkennimpedanz (akustischer Impedanz) Z0 bezeichnet und beschreibt die Bedingungen für die Schallausbreitung durch das Medium. ρ (rho) = Dichte, c = Schallgeschwindigkeit und v = Schallschnelle oder Partikelgeschwindigkeit. Die Einheit für die akustische Impedanz Z0 ist N·s/m³. Wie oben gesehen, ist die Schallkennimpedanz Z0 (Akustische Impedanz) das Verhältnis zwischen dem Schalldruck p und der momentanen Schallschnelle (Partikelgeschwindigkeit) v: Z0 = ρ0 · c = p / v. Die Schallkennimpedanz ist ein wichtiger Faktor bei allen Beurteilungen der Schallwellen, insbesondere beim Vergleich von Schallmessungen in Luft und in Wasser. Für solche Auswertungen ist es üblich, die charakteristische Schallkennimpedanz Z0 wie folgt anzugeben: Bei Luft:Z0 = 413 N·s/m³ oder Pa·s/m bei der Temperatur ϑ (theta) = 20°C bei Standard- Atmosphärendruck. Bei Wasser:Z0 = 1 480 000 N·s/m³ (destilliertes Wasser bei 20°C). Die Ähnlichkeit zwischen den Ohmschen Gesetz für elektrische Berechnungen und den obigen Gleichungen ist eine nützliche Betrachtungsweise für das Verständnis akustischer Berechnungen, wobei die Schallintensität als Leistung (Watt), der Schalldruck als Spannung (Volt) und die Schallkennimpedanz als Widerstand (Ohm) angenommen wird; siehe: "Das Formelrad der Akustik" Schallpegel Der Schallpegel wird nicht direkt durch mathematischen Gleichungen gegeben, sondern hängt von einer Reihe von Faktoren ab, einschließlich der Stärke der Schallwelle, der Frequenz und der Länge der Schalldarbietung und ob der Schall sich im Medium Luft oder Wasser ausbreitet. Die dB-Skala Wegen des großen Bereichs von Schalldrücken und Schallintensitäten bei Schallmessungen, ist es üblich, diesen durch die Verwendung einer logarithmischen Skala auszudrücken. Die am häufigsten verwendete logarithmische Skala für die Beschreibung von Schall ist die Dezibel-Skala (dB). Der absolute Schallintensitätspegel LI einer Schallintensität I ist definiert als: LI = 10 · log (I / I0) in dB, wobei die Schallintensität I in Watt/m² (Watt pro Quadratmeter) angegeben wird und die Referenzschallintensität I0 = 1 pW/m² = 10−12 Watt/m² ist. Merke: log ist der Logarithmus zur Basis 10. Da die Schallintensität proportional zum quadrierten Schalldruck ist, wird der Dezibelausdruck für den absoluten Schalldruckpegel: Lp oder SPL = 10 · log (p² / p0²) = 20 · log (p / p0) in dB (SPL = Sound Pressure Level), wobei der Schalldruck p in Pa (Pascal) oder N/m² gemessen wird und der Referenzschalldruck p0 = 0,00002 Pa = 20 µPa = 20 · 10−6 Pa = 2 · 10−5 Pa ist. Zu beachten ist, dass die Dezibel-Skala ein relatives Maß ist und keine Einheit bei der Schallmessung. Daher können auch andere Maßeinheiten und Referenzpegel anstelle der oben genannten Normen verwendet werden. Bezugszwerte (Referenzwerte) Als Bezugswert (Referenz) für den Schalldruck p0 oder die Schallintensität I0 werden verschiedene Werte für Messungen in Luft und im Wasser eingesetzt. Für Schallmessungen in Luft ist der Referenzschalldruck festgelegt mit: p0 = 20 µPa = 2 · 10−5 Pa = 0,00002 Pa (0,0002 µbar) als Effektivwert (RMS) und die Bezugsschallintensität mit I0 = 10−12 Watt/m². Dieses stellt die untere Grenze der Empfindung des menschlichen Gehörs bei 1000 Hz dar. Das entspricht einem Schallpegel von 0 dB. Für Schallmessungen in Wasser (Unterwasserschall) ist der Referenzschalldruck festgelegt mit: p0 (Wasser) = 1 µPa = 10−6 Pa = 0,000001 Pa (0,00001 µbar). Auch das entspricht 0 dB. Die unterschiedlichen Referenzwerte zwischen den Messungen in Luft und in Wasser sind zu beachten. Der Unterschied zwischen beiden Medien ist 26 dB. Zu den dB-Werten gibt es keine einheitliche Nomenklatur, die aussagt, ob eine Messung in Luft oder in Wasser stattfindet. Daher muss jede Bezugnahme auf einen dB-Wert sorgfältig überprüft werden, um festzustellen, wo die Messung durchgeführt wurde und welcher Referenzpegel verwendet wurde. Es gibt einen physikalischen Unterschied zwischen Schall in Luft und Schall in Wasser, wobei unterschiedliche Referenzpegel verwendet werden. Daher muss beim Vergleich von Schalldruckmessungen in Luft und Wasser ein Korrekturfaktor von 62 dB hinzugefügt werden. |
| zurück |
Suchmaschine |
Startseite |