

| English version |
| Es ist eine unrichtige Annahme, dass die Schallgeschwindigkeit mit der Höhe über dem Meeresspiegel (über Meereshöhe) abnimmt, weil auch die Dichte der Luft mit der Höhe abnimmt. Der ändernde Luftdruck ändert nicht die Schallgeschwindigkeit. Allein die kältere Temperatur (!) lässt die Schallgeschwindigkeit in größeren Höhen abnehmen. Mit der Meereshöhe und dem Luftdruck hat die Schallgeschwindigkeit nichts zu tun und ohne Medium Luft gibt's keine Schallgeschwindigkeit. Die Schallgeschwindigkeit ist so gut wie nur von der Temperatur abhängig. Sie ist nicht abhängig von der Schall-Amplitude, der Frequenz oder der Wellenlänge. |
| Bei 0°C ist ρ0 = 1,293 kg/m3, Z0 = 428 N·s/m3 und c0 = 331,5 m/s Bei 15°C ist ρ15 = 1,225 kg/m3, Z15 = 417 N·s/m3 und c15 = 340 m/s Bei 20°C ist ρ20 = 1,204 kg/m3, Z20 = 413 N·s/m3 und c20 = 343 m/s Bei 25°C ist ρ25 = 1,184 kg/m3, Z25 = 410 N·s/m3 und c25 = 346 m/s |
| Die Schallgeschwindigkeit c in Luft wird durch das Medium Luft bestimmt und ist nicht von der Amplitude, der Frequenz und der Wellenlänge des Schalls abhängig. Bei einem idealen Gas ist die Schallgeschwindigkeit nur von der Temperatur abhängig und unabhängig vom Gasdruck (statischer Luftdruck). Diese Abhängigkeit gilt daher auch für Luft, die in guter Näherung als ideales Gas betrachtet werden kann. Dieses ist eine Seite für Tontechniker und Musiker. Uns interessiert die Schallgeschwindigkeit von Luft (!) auf der Erde an Plätzen an denen akustische Musikinstrumente gespielt oder Gesangsstimmen eingesetzt werden - üblicherweise in Räumen oder Konzertsälen. Es kann hier also nicht um die etwaige Schallgeschwindigkeit in höheren Atmosphären- schichten, wie in 100 km Höhe dicht am Vakuum oder um höheren Luftdruck etwa in Autorreifen gehen. Welche Geschwindigkeit hat Schall im täglichen Leben? |
| Anmerkung für Musiker und Tontechniker aber weniger für Physikprofessoren: Die Schallgeschwindigkeit ändert sich deutlich mit der Temperatur, etwas mit der Luftfeuchtigkeit − aber nicht mit unserem Luftdruck. Die Angabe "Schalldruck auf Meereshöhe" ist falsch und irreführend; dagegen ist die Temperaturangabe hierbei unbedingt notwendig. Der schwankende Luftdruck ändert nicht den Klang von Musikinstrumenten in einem Saal oder in einem Zimmer. Das macht jedoch die ändernde Temperatur. |
| Der mittlere Luftdruck auf Meereshöhe ist 101325 Pa. Jedoch ist diese Angabe bei der Schallgeschwindigkeit unbedeutend. Dazu brauchen wir immer die Temperaturangabe. |
| Google irrt (siehe den folgenden Link) http://productforums.google.com/forum/#!category-topic/websearch/unexpected-search-results/N5JMdZOkeuQ Dieses sagt Google dazu: "Schallgeschwindigkeit auf Meereshöhe = 340.29 m/s". Das ist eine schlechte Antwort, weil die wichtige Temperaturangabe fehlt, und der angegebene Luftdruck "auf Meereshöhe" wirklich keine Bedeutung hat. |
|
In SI-Einheiten ist bei trockener Luft und 20°C (68°F) die Schallgeschwindigkeit c = 343 m/s. Dieses entspricht 1235 km/h (nicht kmh), 767,3 mph, 1125 ft/s (fps) oder 666 Knoten. Das sind 0,343 Kilometer pro Sekunde (km/s) oder 20,58 Kilometer pro Minute (km/min). Es ergibt keinen Sinn, bei der Nennung der Schallgeschwindigkeit den Zusatz "auf Meereshöhe" anzugeben, denn die Schallgeschwindigkeit hängt nicht vom statischen Luftdruck ab; jedoch ist die Temperatur recht wichtig. Begründung: Der statische Luftdruck p_ und die Dichte der Luft ρ sind bei gleicher Temperatur zueinander proportional, weil das Verhältnis p_ / ρ immer konstant ist − auf einem hohen Berg oder selbst auf Meerespiegelhöhe. Merke: Das Verhältnis p_ / ρ (statischer Luftdruck zur Dichte der Luft) ist wirklich immer konstant. Formel: |
Schallgeschwindigkeit 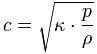 |
| Das heißt, das Verhältnis p_ / ρ ist immer konstant; auf einem hohen Berg und auch auf Meerespiegelhöhe. Der statische Luftdruck p_ und die Dichte der Luft (Luftdichte) ρ sind immer zueinander proportional. Beim Berechnen der Schallgeschwindigkeit vergiss den Luftdruck, aber achte unbedingt auf die Temperatur. Die Schallgeschwindigkeit verändert sich mit der Höhe nur wegen der dortigen Änderung der Lufttemperatur! Druck ist von der Temperatur abhängig und nur indirekt von der Höhe.. |
| Adiabatenexponent (Isentropenexponent) κ (kappa) = cp/cV = 1.402 für Luft. Wärmekapazität bei konstantem Druck = cp; Wärmekapazität bei konstantem Volumen = cv Allgemein gilt mit hinreichender Genauigkeit als Formel für die Schallgeschwindigkeit (Fortpflanzungsgeschwindigkeit) von Luft in m/s in Abhängigkeit von der Temperatur ϑ (theta) in °C:
Das ergibt zum Beispiel bei der Temperatur von ϑ = 20°C eine Schallgeschwindigkeit von: c ≈ 331,5 + (0,6 · ϑ) = 331,5 + (0,6 · 20) = 343,5 m/s.
Es gibt eine brauchbare Formel (Daumenregel), um die Temperatur ϑ in °C zu berechnen, wenn die Schallgeschwindigkeit c (m/s) in Luft bekannt ist. Formel: Temperatur der Luft ϑ ≈ (c − 331,5) / 0,6 in °C. Mit folgender Formel ist die Schallgeschwindigkeit genau zu berechnen. Schallgeschwindigkeit 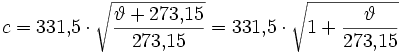 in m/s; in m/s;Temperatur ϑ in °C. |
Schallgeschwindigkeit vs Höhe und Temperatur?
Vergiss die Höhe und kümmere dich nur um die Temperatur.
| Bei der Temperatur von ϑ = 0°C wurde die Schallgeschwindigkeit in trockener Luft mit c = 331,5 m/s bestimmt. Genaue Gleichungen zur Schallgeschwindigkeit und der Temperatur: Zu berechnen ist die genaue Schallgeschwindigkeit in m/s: c = 331,5 · √ (1+(ϑ / 273,15)) wenn die bekannte Lufttemperatur ϑ in °C eingesetzt wird. Zu berechnen ist die genaue Temperatur der Luft in °C: ϑ = 273,15 · (0,0000090998227809513409726345579419841 · c2 − 1) wenn die bekannte Schallgeschwindigkeit c in m/s eingesetzt wird. Vereinfachte Formeln (für +35°C bis −35°C): Schallgeschwindigkeit in Luft in m/s: c = 331,5 + 0,6 · ϑ Temperatur in °C: ϑ = (c − 331,5) / 0,6 |
Umrechnung: Luft-Temperatur in Schallgeschwindigkeit
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Die Schallgeschwindigkeit c ist von der Temperatur der Luft ϑ abhängig und nicht vom Luftdruck p! Die Luftfeuchtigkeit hat geringe vernachlässigbare Auswirkung auf die Schallgeschwindigkeit. Merke: Der Luftdruck und die Luftdichte sind bei gleicher Temperatur zueinander proportional. Immer ist das Verhältnis p_ / ρ = konstant. Rho ist die Dichte ρ und p_ ist der statische Luftdruck. Damit geht der Luftdruck nicht in die Berechnung der Schallgeschwindigkeit von Luft ein. |
| Merke: Die Schallgeschwindigkeit ist auf einer Bergspitze sowie auf Meereshöhe (Meeresspiegel) genau gleich, vorausgesetzt wir haben die gleiche Lufttemperatur. Anzunehmen ist, dass dieses selbst in 100 km Höhe zutrifft. Mit abnehmendem Luftdruck nimmt auch die Dichte der Luft ab. |
Bei welcher Temperatur hat die Schallgeschwindigkeit den doppelten Wert von 0°C?
| Bei welcher Temperatur wird die Schallgeschwindigkeit c = 331.5 m/s verdoppelt? Eine Temperatur von 819.45°C verdoppelt die Schallgeschwindigkeit auf 663 m/s. |
| Siehe die folgende häufige Frage: "Wie groß ist die Schallgeschwindigkeit?" Die Schallgeschwindigkeit, die Temperatur ... und nicht der Luftdruck Dichte der Luft (Luftdichte) ρ = Luftdruck p_ ÷ (Gaskonstante R × Temperatur in Kelvin) ρ = p_ / R × T in kg/m3. Die spezifische Gaskonstante für trockene Luft ist R = 287,058 J/kg · K Joule J = Newton · Meter = N·m und T in Kelvin = °C + 273,15 Atmosphärischer Druck (Luftdruck) p0 = 101325 Pa = 1013,25 mbar = 1013,25 hPa R = 287,058 J/kg · K T0 = 273,15 K bei 0 °C ρ0 = 101325 / (287,058 · 273,15) = 1,2922 kg/m³ T20 = 293,15 K bei 20 °C ρ20 = 101325 / (287,058 · 293,15) = 1,2041 kg/m³ Bisweilen wird falsch angenommen, dass der Luftdruck und die Luftdichte das Gleiche seien. |
| Die Schallgeschwindigkeit wird Mach 1 genannt. Mach wird verwendet, um die Geschwindigkeit für Objekte, wie Flugzeuge oder Raketen anzugeben, wenn diese mit der Geschwindigkeit der Schallgeschwindigkeit oder ein Vielfaches davon fliegen. Die Geschwindigkeit höher als Mach 1 heißt Überschallgeschwindigkeit. |
| Mach-Zahl unter 1 bedeutet, dass die Strömungsgeschwindigkeit geringer als die Schallgeschwindigkeit ist. Diese Geschwindigkeit wird Unterschall genannt. Mach-Zahl = 1 bedeutet, dass die Strömungsgeschwindigkeit gleich der Schallgeschwindigkeit ist und die Geschwindigkeit "transonic" genannt wird. Mach-Zahl über 1 bedeutet, dass die Strömungsgeschwindigkeit höher als die Schallgeschwindigkeit ist und die Geschwindigkeit wird Überschallgeschwindigkeit genannt. Mehr als Mach-Zahl 5 heißt Hyperschall. Die Mach-"Zahl" ist ein dimensionsloses Verhältnis. |
| Merke: Die Schallgeschwindigkeit c ist unabhängig von der Frequenz und der Amplitude der Schallwelle und vom Luftdruck. Die Schallgeschwindigkeit ist jedoch abhängig von der Temperatur. Bei einer Temperatur von 819.45°C haben wir eine Schallgeschwindigkeit von 663 m/s. Das ist die doppelte Schallgeschwindigkeit, die wir bei 0°C mit 331.5 m/s haben. |
Auch die Überschallgeschwindigkeit hat
|
Tabelle: Die deutliche Wirkung der Temperatur
Die Luftdichte, die Schallgeschwindigkeit und die Charakteristische
Akustische Impedanz in Abhängigkeit von der Temperatur der Luft
| Temperatur der Luft ϑ in °C |
Schallgeschwindigkeit c in m/s |
Zeit pro 1 m Δ t in ms/m |
Luftdichte ρ in kg/m3 |
Schallkennimpedanz von Luft Z in Ns/m3 |
| +40 | 354,94 | 2,817 | 1,1272 | 400,0 |
| +35 | 352,17 | 2,840 | 1,1455 | 403,4 |
| +30 | 349,29 | 2,864 | 1,1644 | 406,7 |
| +25 | 346,39 | 2,888 | 1,1839 | 410,0 |
| +20 | 343,46 | 2,912 | 1,2041 | 413,6 |
| +15 | 340,51 | 2,937 | 1,2250 | 417,1 |
| +10 | 337,54 | 2,963 | 1,2466 | 420,8 |
| +5 | 334,53 | 2,990 | 1,2690 | 424,5 |
| 0 | 331,50 | 3,017 | 1,2920 | 428,3 |
| −5 | 328,44 | 3,044 | 1,3163 | 432,3 |
| −10 | 325,35 | 3,073 | 1,3413 | 436,4 |
| −15 | 322,23 | 3,103 | 1,3673 | 440,6 |
| −20 | 319,09 | 3,134 | 1,3943 | 444,9 |
| −25 | 315,91 | 3,165 | 1,4224 | 449,4 |
Zu beachten: Luftdruck p und Luftdichte ρ sind nicht das gleiche.
Nur wegen der mit der Höhe abnehmenden Lufttemperatur sinkt auch die Schallgeschwindigkeit.
In Gasen, ist die Tonhöhe umso höher, je höher die Schallgeschwindigkeit im Medium ist.
| Schallgeschwindigkeit c in bekannten Materialien |
||
| Medium | m/s | |
| Luft, trocken (20 °C) | 343 | |
| Wasserstoff (0 °C) | 1280 | |
| Wasser (15 °C) | 1500 | |
| Blei | 2160 | |
| Beton | 3100 | |
| Holz (weich, längs der Fasern) | 3800 | |
| Glas | 5500 | |
| Stahl | 5800 | |
| Sind an einer Tonerzeugung Luftsäulenschwinger, wie Holzbläser, Blechbläser oder Orgelpfeifen beteiligt, so ändert sich die Tonhöhe der Instrumente mit der Temperatur und wird als Verstimmung hörbar. Steigende Temperatur erwirkt dabei steigende Tonhöhe und umgekehrt. Beispielsweise ergibt eine Änderung der Temperatur um 1°C etwa 0,75 Hz Frequenzänderung (Verstimmung) bei einer Tonhöhe von 440 Hz (Kammerton a'). |
| Auf die häufige Frage: "Wie groß ist die Schallgeschwindigkeit?", muss immer die Nachfrage folgen: "Bei welcher Temperatur denn?" Wer hierbei den Luftdruck erwähnt, der hat noch etwas zu lernen. |
| In einem gegebenen idealen Gas hängt die Schallgeschwindigkeit c nur von seiner Temperatur ab. Die Schallgeschwindigkeit beträgt in unbewegter trockener Luft bei einer Temperatur von ϑ = 0 Grad Celsius c = 331,5 m/s. Sie hängt von der Temperatur und dem Material ab. Da Schall leichter durch dicht gepackte Moleküle übertragen wird, ist er schneller in dichteren Stoffen. Somit steigt die Schallgeschwindigkeit mit der Steifigkeit des Materials und nicht mit dem Luftdruck. |
| Die internationalen Druckeinheiten Umrechnung von Druckeinheiten Weitere Umrechnung der Druckeinheiten |
| Siehe auch: Dennis A. Bohn, "Environmental Effects on the Speed of Sound" |
Schallgeschwindigkeit in Luft, Frequenz und Wellenlänge
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Bei 0° Celsius ist die Schallgeschwindigkeit in deutschen Lehrbüchern 331,5 m/s. Bei 20° Celsius ist die Schallgeschwindigkeit dann 343,42 m/s, gerundet 343 m/s. Bei 0° Celsius ist die Schallgeschwindigkeit in USA-Lehrbüchern 331,3 m/s. Bei 20° Celsius ist die Schallgeschwindigkeit dann 343,21 m/s, gerundet 343 m/s. |
Umrechner: Celsius nach Fahrenheit und Fahrenheit nach Celsius
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Schalldruck ist die schnelle örtliche Druckänderung beim atmosphärischen Druck, verursacht durch Schallwellen. Der Schall(wechsel)druck in Luft kann mit einem Mikrofon gemessen werden. Die SI-Einheit für den Schalldruck p ist das Pascal – Symbol: Pa |
| Die NASA sagt: Die Schallgeschwindigkeit ist von der Temperatur der Luft abhängig. Sie verändert sich mit der Höhe nur wegen der Änderung der Lufttemperatur! Der statische Luftdruck ist proportional zur Luftdichte (Dichte der Luft). Deshalb haben beide Werte keinen Einfluss auf die Schallgeschwindigkeit. |
| "Speed of sound": http://www.grc.nasa.gov/WWW/k-12/airplane/sound.html "Speed of sound": http://www.grc.nasa.gov/WWW/BGH/sound.html "Atmos Modeler Simulator": http://www.grc.nasa.gov/WWW/k-12/airplane/atmosi.html "Variables that affect the speed of sound" (Quicktime): http://www.nasa.gov/audience/foreducators/topnav/materials/listbytype/Variables_That_Affect_the_Speed.html "Speed of Sound Derivation": http://www.grc.nasa.gov/WWW/BGH/snddrv.html "Mach number": http://www.grc.nasa.gov/WWW/k-12/airplane/mach.html |
| Die Schallgeschwindigkeit in Luft bei 0°C kann berechnet werden: c = (1,4·(287,058 J/K·kg)·(273,15 K))^1/2 = 331,3 m/s, wobei κ (kappa) = 1,4 und die Spezifische Gaskonstante von trockener Luft R = 287,058 (J/K·kg) ist. Die Schallgeschwindigkeit in Luft bei 20°C kann berechnet werden: c = (1,4·(287,058 J/K kg)·(293,15 K))^1/2 = 343.24 m/s. |
| Vertikales Profil der Temperatur der Atmosphäre im Juni bei 45° Nord 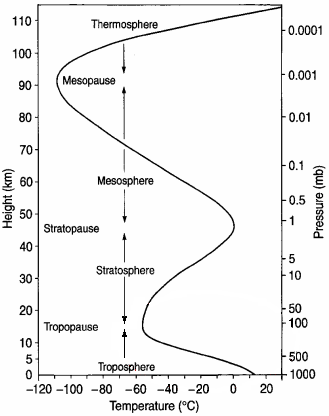 Temperatur in Abhängigkeit von der Höhe (Luftdruck) |
| Falsches Denken: Berechne die Schallgeschwindigkeit in großen Höhen. Man nimmt häufig an, dass das etwas mit der Höhe zu tun haben muss. Das ist jedoch nicht richtig. Allein die Temperatur hat mit der Größe der Schallgeschwindigkeit zu tun. Es ist schon recht kalt da oben. |
| Der Schalldruck (Wechseldruck) ist ein dynamischer Druck. Dagegen ist der Luftdruck (atmosphärischer Gleichdruck) ein statischer Druck. Dem statischen Luftdruck ist der dynamische Schalldruck überlagert. |
| Anmerkung: Die Zeit, die Frequenz und die Phase gehören eng zusammen. Jedoch hat die Höhe der Amplitude keinen Einfluss auf diese Parameter. Die Amplitude A hat nichts mit der Frequenz, der Wellenlänge, der Zeitdauer und der Geschwindigkeit des Schalls zu tun. |
| zurück |
Suchmaschine |
Startseite |