

| English version |
|
Diese Berechnung folgt den Angaben von Owen Cramer, "JASA, 93, S. 2510, 1993" und dem gesättigten
Dampfdruck (Wasserdampf) aus Richard S. Davis, "Metrologia, 29, S. 67, 1992", bei einem Mol-Anteil
von Kohlendioxid von 0,0004. Gültigkeitsbereich: von 0 bis 30°C (273,15 − 303,15K) und für der Luftdruckbereich von 75 und 102 kPa. Im Luftdruckbereich zwischen 95 und 104 kPa ergibt sich so gut wie keine Änderung der Schallgeschwindigkeit c. Der Standard-Luftdruck (atmosphärischer Druck) ist 101325 Pa = 101,325 kPa oder 1013,25 Hektopascal. c kommt von lateinisch celeritas, zu Deutsch Schnelligkeit. |
| Die Schallgeschwindigkeit in Luft wird durch das Medium Luft bestimmt und ist nicht
von der Amplitude, der Frequenz und der Wellenlänge des Schalls abhängig. Bei einem idealen Gas ist die Schallgeschwindigkeit nur von der Temperatur abhängig und unabhängig vom Gasdruck. Diese Abhängigkeit gilt daher auch recht gut für Luft, die in guter Näherung als ideales Gas betrachtet werden kann. Auswirkungen der Umgebung verändern die Geschwindigkeit des Schalls und der Absorption von Schall in Luft. Selbst geringe prozentuale Veränderungen bringen Probleme beim Hören in geschlossenen akustischen Räumen. Der Luftdruck (atmosphärischer Druck) wird hier trotzdem eingegeben, falls man einmal einen weit vom Normalen vorkommenden Druck in die Rechnung einbeziehen muss. Und nicht vergessen, dieses ist eine Webseite für Soundesigner und Tontechniker. |
Bei Dezimal-Eingabe ist der Punkt zu verwenden.
| Anmerkung für Musiker und Tontechniker aber weniger für Physikprofessoren: Die Schallgeschwindigkeit ändert sich deutlich mit der Temperatur, etwas mit der Luftfeuchtigkeit − aber nicht mit unserem Luftdruck. Die Angabe "Schalldruck auf Meereshöhe" ist falsch und irreführend; dagegen ist die Temperaturangabe hierbei unbedingt notwendig. Der schwankende Luftdruck ändert nicht den Klang von Musikinstrumenten in einem Saal oder in einem Zimmer. Das macht jedoch die ändernde Temperatur. Sie ist nicht abhängig von der Schall-Amplitude, der Frequenz oder der Wellenlänge. Weil in den Rechner der Luftdruck eingegeben wird, gibt hier doch keinen Widerspruch, denn im Luftdruckbereich zwischen 98 und 104 kPa ergeben sich so gut wie keine Änderungungen der Schallgeschwindigkeit. Bei den Luftdruckzuständen in denen sich ein Violinist oder ein Klarinettist wohlfühlt, sind keine merkbaren Änderungen der Schallgeschwindigkeit festzustellen. |
| Der mittlere Luftdruck auf Meereshöhe ist 101325 Pa. Jedoch ist diese Angabe bei der Schallgeschwindigkeit unbedeutend. Dazu brauchen wir immer die Temperaturangabe. |
| Google irrt (siehe den folgenden Link) http://productforums.google.com/forum/#!category-topic/websearch/unexpected-search-results/N5JMdZOkeuQ Dieses sagt Google dazu: "Schallgeschwindigkeit auf Meereshöhe = 340.29 m/s". Das ist eine schlechte Antwort, weil die wichtige Temperaturangabe fehlt, und der angegebene Luftdruck "auf Meereshöhe" wirklich keine Bedeutung hat. |
| Es ist eine unrichtige Annahme, dass die Schallgeschwindigkeit mit derHöhe
über dem Meeresspiegel (über Meereshöhe) abnimmt, weil auch die Dichte
der Luft mit der Höhe abnimmt. Der ändernde Luftdruck ändert nicht die
Schallgeschwindigkeit. Allein die kältere Temperatur (!) lässt die Schallgeschwindigkeit in größeren Höhen abnehmen. Mit der Meereshöhe und dem Luftdruck hat die Schallgeschwindigkeit nichts zu tun und ohne Medium Luft gibt's keine Schallgeschwindigkeit. Die Schallgeschwindigkeit ist so gut wie nur von der Temperatur abhängig. |
| In SI-Einheiten ist bei trockener Luft und 20°C (68 °F) die Schallgeschwindigkeit c = 343 m/s. Dieses entspricht 1235 km/h (nicht kmh), 767 mph, 1125 ft/s oder 666 Knoten. Das sind 0,343 Kilometer pro Sekunde (km/s) oder 20,58 Kilometer pro Minute (km/min). Bei der Temperatur von ϑ = 0°C wurde die Schallgeschwindigkeit in trockener Luft mit c = 331,5 m/s bestimmt. Es ergibt keinen Sinn, bei der Nennung der Schallgeschwindigkeit den Zusatz "auf Meereshöhe" anzugeben, denn die Schallgeschwindigkeit hängt nicht vom statischen Luftdruck ab; jedoch ist die Temperatur recht wichtig. Begründung: Der statische Luftdruck p_ und die Dichte der Luft ρ sind bei gleicher Temperatur zueinander proportional, weil das Verhältnis p_ / ρ immer konstant ist − auf einem hohen Berg oder selbst auf Meerespiegelhöhe. |
Schallgeschwindigkeit 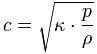 |
| Das heißt, das Verhältnis p_ / ρ ist immer konstant; auf einem hohen Berg und auch auf Meerespiegelhöhe. Der statische Luftdruck p_ und die Dichte der Luft (Luftdichte) ρ sind immer zueinander proportional. Beim Berechnen der Schallgeschwindigkeit vergiss den Luftdruck, aber achte unbedingt auf die Temperatur. Die Schallgeschwindigkeit verändert sich mit der Höhe nur wegen der dortigen Änderung der Lufttemperatur! Druck ist von der Temperatur abhängig und nur indirekt von der Höhe.. |
| Die Schallgeschwindigkeit wird Mach 1 genannt. Mach wird verwendet, um die Geschwindigkeit für Objekte, wie Flugzeuge oder Raketen anzugeben, wenn diese mit der Geschwindigkeit der Schallgeschwindigkeit oder ein Vielfaches davon fliegen. Die Geschwindigkeit höher als Mach 1 heißt Überschallgeschwindigkeit. |
| Mach-Zahl unter 1 bedeutet, dass die Strömungsgeschwindigkeit geringer ist als die Schallgeschwindigkeit ist und die Geschwindigkeit wird Unterschall genannt. Mach-Zahl = 1 bedeutet, dass die Strömungsgeschwindigkeit gleich der Schallgeschwindigkeit ist und die Geschwindigkeit wird "transonic" genannt. Mach-Zahl über 1 bedeutet, dass die Strömungsgeschwindigkeit höher als die Schallgeschwindigkeit ist und die Geschwindigkeit wird Überschallgeschwindigkeit genannt. Mehr als Mach-Zahl 5 heißt Hyperschall. Die Mach-"Zahl" ist ein dimensionsloses Verhältnis. |
| M < 1: Subsonic flow M = 1: Sonic flow M > 1: Supersonic flow |
| Machzahl | M < 0.3 | 0.3 < M < 1 | M = 1 | M ≈ 1 | 1 < M < 5 | 5 < M |
| Name | Low subsonic | High subsonic | Sonic | Transonic | Supersonic | Hypersonic |
| Merke: Die Schallgeschwindigkeit c ist unabhängig von der Frequenz und der Amplitude der Schallwelle und vom Luftdruck. Die Schallgeschwindigkeit ist jedoch abhängig von der Temperatur. |
Auch die Überschallgeschwindigkeit hat absolut nichts mit dem Luftdruck zu tun - wohl aber mit der Temperatur!
|
| Frequenzabhängige Luftdämpfung (dB) in 30 m Abstand bei unterschiedlicher Luftfeuchtigkeit (Prozent) |
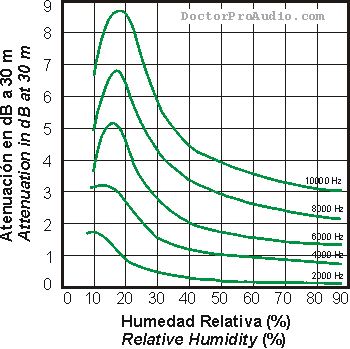 |
Bild mit freundlicher Genehmigung von DoctorProAudio.com Die Konsistenz der Luftfeuchtigkeit ist bei Tonaufnahmen wichtig. Es gibt keine ideale Luftfeuchtigkeit. |
Berechnungen zur Luftdichte (Dichte der Luft)
Betrachten wir zuerst das ideale Gasgesetz:
(1) p · V = n · R · T
| p = Druck in Pascal, multipliziere Millibar (mb) mit 100 |
| V = Volumen in m3 |
| n = Mol-Anzahl |
| R = Spezifische Gaskonstante |
| T = Kelvin-Temperatur K = °C + 273,15 |
Die Dichte ist die Anzahl der Moleküle eines idealen Gases bei einem bestimmten Volumen.
In diesem Falle kann ein Mol-Volumen mathematisch ausgedrückt werden als:
(2) D = ρ = n / V
| D = ρ = Dichte in kg/m3 |
| n = Anzahl der Moleküle |
| V = Volumen in m3 |
Indem man die vorherigen beiden Gleichungen kombiniert, wird der Ausdruck für die Dichte zu:
(3) ![]()
| D = ρ = Dichte in kg/m3 |
| p = Druck in Pascal (multipliziere mb mit 100) |
| R = Spezifische Gaskonstante 287,058 J / (kg · K) für trockene Luft |
| T = Temperatur K = °C + 273,15 |
Die Luftdichte kann mit den Standard-Meereshöhe-Bedingungen mit
p = 101325 Pa und T = 15 °C berechnet werden:
D = ρ = 101325 / (287,058 · (15 + 273,15)) = 1,2250 kg/m3
Dieses Beispiel gilt für die Standard-Bedingungen bei trockener Luft. In der Wirklichkeit
muss man verstehen, wie die Dichte durch die Feuchtigkeit der Luft (Luftfeuchte) beeinflusst wird.
Die Dichte ρ = D aus der Mischung von trockenen Luft-Molekülen und Wasserdampf-Molekülen ist:
(4) ![]()
| D = ρ = Dichte in kg/m3 |
| pd = Druck von trockener Luft in Pascal |
| pv = Druck von Wasserdampf in Pascal |
| Rd = Gaskonstante für trockene Luft = 287,058 J / (kg · K) |
| Rv = Gaskonstante für Wasserdampf = 461,495 J / (kg · K) |
| T = Temperatur K = °C + 273,15 |
Um die Dichte von Luft (Luftdichte) zu bestimmen, muss der wirkliche Luftdruck
(Absoluter Druck), der Wasserdampfdruck und die Temperatur bekannt sein.
| Umrechnung der dB zwischen Luft und Wasser |
| Im Jahr 1970 wurde der Schalldruck-Bezugspegel von 0 dB = 1 Mikropascal von der
US Navy für Arbeiten im Wasser (Wasserschall) gewählt. Näherungsweise unterscheiden sich gleiche Pegelangaben für Luft und Wasser bei ihrem jeweiligen Referenzdruck in ihrem Pegel um etwa 62 dB. Für eine - ohnehin fragliche - Vergleichbarkeit sind also vom Wasserschall etwa 62 dB abzuziehen. |
Was ist ein Millibar? Millibar (mbar) ist die veraltete Einheit für den Luftdruck
- heute Hektopascal, dabei entspricht 1 hPa = 1 mbar
Der Standard-Luftdruck ist 101325 Pa = 101,325 kPa oder 1013,25 Hektopascal.
Berechnung der Wellenlänge mit Frequenz und Temperatur
Berechnung der Wellenlänge von Radiowellen und Schallwellen
Tabelle: Die deutliche Wirkung der Temperatur
Die Luftdichte, die Schallgeschwindigkeit und die Charakteristische
Akustische Impedanz in Abhängigkeit von der Temperatur der Luft
| Temperatur der Luft ϑ in °C |
Schallgeschwindigkeit c in m/s |
Zeit pro 1 m Δ t in ms/m |
Luftdichte ρ in kg/m3 |
Schallkennimpedanz von Luft Z0 in Ns/m3 |
| +40 | 354,94 | 2,817 | 1,1272 | 400,0 |
| +35 | 352,17 | 2,840 | 1,1455 | 403,4 |
| +30 | 349,29 | 2,864 | 1,1644 | 406,7 |
| +25 | 346,39 | 2,888 | 1,1839 | 410,0 |
| +20 | 343,42 | 2,912 | 1,2041 | 413,6 |
| +15 | 340,51 | 2,937 | 1,2250 | 417,1 |
| +10 | 337,54 | 2,963 | 1,2466 | 420,8 |
| +5 | 334,53 | 2,990 | 1,2690 | 424,5 |
| 0 | 331,50 | 3,017 | 1,2920 | 428,3 |
| −5 | 328,44 | 3,044 | 1,3163 | 432,3 |
| −10 | 325,35 | 3,073 | 1,3413 | 436,4 |
| −15 | 322,23 | 3,103 | 1,3673 | 440,6 |
| −20 | 319,09 | 3,134 | 1,3943 | 444,9 |
| −25 | 315,91 | 3,165 | 1,4224 | 449,4 |
ϑ = Temperatur in °C, c = Schallgeschwindigkeit, ρ = Dichte,
Z0 = ρ · c = Kennwiderstand (Spezifische akustische Impedanz) von Luft
Schalldruck p = √ (I × Z0) und Schallintensität I = p² / Z0 ρ = 101325 / (287,058 · (273,15 + ϑ))
Standard-Luftdruck p0 = 101325 Pa, Spezifische Gaskonstante R = 287,058 J/kg · K.
Nur wegen der mit der Höhe abnehmenden Lufttemperatur sinkt auch die Schallgeschwindigkeit.
Umrechner: Temperatur und Schallgeschwindigkeit in Luft
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Die Schallgeschwindigkeit in Wasser
Die Schallgeschwindigkeit in Wasser ist etwa 1480 m/s. Es ist möglich die Änderungen der
Ozeantemperatur zu messen, indem man die Änderung der Schallgeschwindigkeit über große
Entfernungen feststellt. Die Schallgeschwindigkeit in Ozean-Wasser ist etwa:
![]()
wobei T die Temperatur in °C, S der Salzgehalt in psu und D die Tiefe in Metern ist.
Änderung der Schallgeschwindigkeit mit der Höhe
| Die Standard-Tabelle "Schallgeschwindigkeit bei unterschiedlicher Höhe" "Speed of Sound at Different Altitudes" Die Schallgeschwindigkeit ist keine Konstante, sondern hängt allein von der tatsächlichen Temperatur in dieser Höhe ab. Die Aussage, dass die Schallgeschwindigkeit mit der Höhe über Grund zusammenhängt ist falsch. Die Schallgeschwindigkeit ändert sich allein mit der Temperatur. Klar, es ist eben recht kalt dort oben. |
Änderung des Luftdrucks mit der Höhe
| Frage: Wie ändert sich der Luftdruck, wenn sich die Höhe um 1Meter ändert? Der hydrostatische Druck berechnet sich nach Blaise Pascal: Dieses Gesetz wird auch für eine Luftsäule angenommen. Höhe h = 1 m Normfallbeschleunigung nach DIN 1305 ist g = 9,80665 m/s2. Dichte der Luft bei 20°C ist ρ20 = 1,204 kg/m3. Bei 1 m Höhenänderung ändert sich der Luftdruckum: p = ρ20 ∙ g ∙ h = 1,204 kg/m3 ∙ 9,80665 m/s2 ∙ 1 m = 11,8 Pa (N/m2). Faustformel: In Bodennähe nimmt der Luftdruck bei - konstaner Temperatur von 20°C - um 1 hPa = 100 Pa bei einer Höhenänderung von h = 8,5 m ab. Die Temperatur nimmt jedoch in der Tendenz mit der Höhe ab. |
Umrechner: Celsius nach Fahrenheit und Fahrenheit nach Celsius
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |

| zurück |
Suchmaschine |
Startseite |