

| English version |
Tabelle: Die deutliche Wirkung der Temperatur
Die Luftdichte, die Schallgeschwindigkeit und die Charakteristische
Akustische Impedanz in Abhängigkeit von der Temperatur der Luft
| Temperatur der Luft ϑ in °C |
Schallgeschwindigkeit c in m/s |
Zeit pro 1 m Δ t in ms/m |
Luftdichte ρ in kg/m3 |
Schallkennimpedanz von Luft Z0 in Ns/m3 |
| +40 | 354,94 | 2,817 | 1,1272 | 400,0 |
| +35 | 352,17 | 2,840 | 1,1455 | 403,4 |
| +30 | 349,29 | 2,864 | 1,1644 | 406,7 |
| +25 | 346,39 | 2,888 | 1,1839 | 410,0 |
| +20 | 343,42 | 2,912 | 1,2041 | 413,5 |
| +15 | 340,51 | 2,937 | 1,2250 | 417,1 |
| +10 | 337,54 | 2,963 | 1,2466 | 420,8 |
| +5 | 334,53 | 2,990 | 1,2690 | 424,5 |
| ±0 | 331,50 | 3,017 | 1,2920 | 428,3 |
| −5 | 328,44 | 3,044 | 1,3163 | 432,3 |
| −10 | 325,35 | 3,073 | 1,3413 | 436,4 |
| −15 | 322,23 | 3,103 | 1,3673 | 440,6 |
| −20 | 319,09 | 3,134 | 1,3943 | 444,9 |
| −25 | 315,91 | 3,165 | 1,4224 | 449,4 |
ϑ = Temperatur in °C, c = Schallgeschwindigkeit, ρ = Dichte,
Z0 = ρ · c = Kennwiderstand (Spezifische akustische Impedanz) von Luft
Schalldruck p = √ (I × Z0) und Schallintensität I = p² / Z0 ρ = 101325 / (287,058 · (273,15 + ϑ))
Standard-Luftdruck p0 = 101325 Pa, Spezifische Gaskonstante R = 287,058 J/kg · K.
Nur wegen der mit der Höhe abnehmenden Lufttemperatur sinkt auch die Schallgeschwindigkeit.
| Als Bezugsgröße ist die akustische Kennimpedanz der umgebenden Luft (Schallkennimpedanz) einheitlich mit
dem runden Wert Z0 = 400 N·s/m³ (Pa·s/m) in der Physik (Akustik) eingeführt - ohne
dabei auf eine bestimmte Temperatur einzugehen. Bei diesem runden Wert stimmt der "Schallpegel" als Dezibel-Wert, also der Schalldruckpegel mit dem Schallintensitätspegel genau überein. Die Bezugs-Schallkennimpedanz Z0 = ρ · c = 400 N·s/m³ berechnet sich aus den Werten der Hörschwelle von Schalldruck p0 = 20 µPa (µN/m²) und der Schallintensität I0 = 1 pW/m². Schalldruckpegel und Schallintensitätspegel sind also bei einer Schallkennimpedanz von Z0 = 400 N·s/m³ absolut identisch. |
| Die Schallgeschwindigkeit in Luft c wird durch das Medium Luft bestimmt und ist nicht von der Amplitude, der Frequenz und der Wellenlänge des Schalls abhängig. Bei einem idealen Gas ist die Schallgeschwindigkeit nur von der Temperatur abhängig und unabhängig vom Gasdruck. Diese Abhängigkeit gilt daher auch für Luft, die in guter Näherung als ideales Gas betrachtet werden kann. |
| Merke: Die Schallgeschwindigkeit ändert sich deutlich mit der Temperatur, etwas mit der Luftfeuchtigkeit − aber nicht mit unserem Luftdruck. Die Angabe "Schalldruck auf Meereshöhe" ist falsch und irreführend. Die Temperaturangabe ist dazu jedoch unbedingt notwendig. |
| Der mittlere Luftdruck auf Meereshöhe ist 101325 Pa. Jedoch ist diese Angabe bei der Schallgeschwindigkeit unbedeutend. Dazu brauchen wir immer die Temperaturangabe. |
Schallgeschwindigkeit in Luft
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Bei 0° Celsius ist die Schallgeschwindigkeit in deutschen Lehrbüchern 331,5 m/s. Bei 20° Celsius ist die Schallgeschwindigkeit dann 343,42 m/s, gerundet 343 m/s. Bei 0° Celsius ist die Schallgeschwindigkeit in USA-Lehrbüchern 331,3m/s. Bei 20° Celsius ist die Schallgeschwindigkeit dann 343,21 m/s, gerundet 343 m/s. |
Die Wirkung der Temperatur
|
Die Luftdichte ist: ρ = p / (R · T) in kg/m3, Luftdruck = p, Gaskonstante = R, Temperatur in Kelvin = T Die individuelle Gaskonstante R für trockene Luft ist: R = 287,058 J / kg · K mit Energie Joule (J) = Newton · Meter = N m; T in Kelvin = Temperatur in °C + 273,15. Atmosphärischer Luftdruck p0 = 101325 Pa = 1013,25 mbar = 1013,25 hPa und R = 287,058 J/kg · K. Bei T0 = 273,15 K (0 °C) (Normalbedingungen) ist die Luftdichte: ρ0 = 101325 / (287,058 · 273,15) = 1,2922 kg/m3. Bei T25 = 298,15 K (25 °C) (Standardbedingungen) ist die Luftdichte: ρ25 = 101325 / (287,058 · 298,15) = 1,184 kg/m3. Weiterhin ist üblich T20 = 293,15 K ↔ 20°C und dabei ist die Luftdichte ρ = 1,2041 kg/m3. Wie man erkennt, sind diese Größen deutlich temperaturabhängig. Die Schallgeschwindigkeit in Luft ist temperaturabhängig: 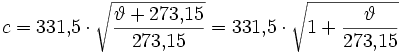 ϑ (theta) ist die Temperatur in °C. Z0 = ρ0 · c0 Hierbei ist Z0 die Schallkennimpedanz von Luft und c ist die Schallgeschwindigkeit. In SI-Einheiten ist bei trockener Luft und 20°C (68 °F) die Schallgeschwindigkeit c = 343 m/s. Dieses entspricht 1235 km / h (nicht kmh), 767 mph, 1125 ft / s oder 666 Knoten. |
| Google irrt (siehe den folgenden Link) http://productforums.google.com/forum/#!category-topic/websearch/unexpected-search-results/N5JMdZOkeuQ Dieses ist die falsche Antwort von Google: "Schallgeschwindigkeit auf Meereshöhe = 340.29 m/s". Das ist eine zumindest schlechte Antwort, weil die wichtige Temperaturangabe fehlt, und der angegebene Luftdruck "auf Meereshöhe" wirklich keine Bedeutung hat. |
| Begründung: Der statische Luftdruck p_ und die Dichte ρ der Luft sind bei gleicher Temperatur zueinander proportional. Das Verhältnis p / ρ ist immer konstant; auf einem hohen Berg oder selbst auf Meerespiegelhöhe. Beim Berechnen der Schallgeschwindigkeit vergiss den Luftdruck, aber achte unbedingt auf die wichtige Temperatur. Die Schallgeschwindigkeit verändert sich mit der Höhe nur wegen der Änderung der Lufttemperatur! |
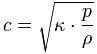 |
| Adiabatenexponent (Isentropenexponent) κ (kappa) = cp/cV.
Allgemein gilt mit hinreichender Genauigkeit als Formel für die Schallgeschwindigkeit (Fortpflanzungsgeschwindigkeit) von Luft in m/s in Abhängigkeit von der Temperatur ϑ (theta) in °C:
Das ergibt zum Beispiel bei ϑ = 20 °C eine Schallgeschwindigkeit von c = 331,3 + (0,606 · 20) = 343,42 m/s. Oft genügt als Formel: c ≈ 331 + (0,6 · 20) = 343 m/s.
|
| Es gibt eine brauchbare Formel (Daumenregel), um die Temperatur ϑ (°C) zu berechnen, wenn die Schallgeschwindigkeit c (m/s) in Luft bekannt ist. Formel: Temperatur der Luft ϑ ≈ (c − 331) / 0,6 in °C. Mit folgender Formel ist die Schallgeschwindigkeit genauer zu berechnen. Schallgeschwindigkeit 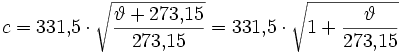 in m/s; in m/s;Temperatur ϑ in °C. Temperatur der Luft ϑ°C = 273,15 · (0,000009099822780951 · c² − 1) in °C. Schallgeschwindigkeit c = 331,5 · sqrt (1+(ϑ°C / 273.15)) |
Formel: Temperatur der Luft ϑ = 273,15·(0,00000909981·c2 − 1) in °C.
Umrechnung: Schallgeschwindigkeit und Luft-Temperatur
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Die Schallgeschwindigkeit c ist von der Temperatur der Luft abhängig und nicht vom Luftdruck p! Die Luftfeuchtigkeit hat geringe vernachlässigbare Auswirkung auf die Schallgeschwindigkeit. Merke: Der Luftdruck und die Luftdichte sind bei gleicher Temperatur zueinander proportional. Immer ist das Verhältnis p_ / ρ = konstant. Rho ist die Dichte ρ und p_ ist der statische Luftdruck. Damit geht der Luftdruck nicht in die Berechnung der Schallgeschwindigkeit von Luft ein. |
| Merke: Die abgestrahlte Schallleistung (Schallintensität) ist die Ursache - und der Schalldruck ist die Wirkung. Die Schallwirkung interessiert insbesondere den Tontechniker. Die Wirkung der Temperatur und des Schalldrucks. |
| Akustiker und Schallschützer ("Lärmbekämpfer") brauchen die Schall- intensität und die Schallleistung – jedoch benötigen Tontechniker und Sound-Designer ("Ohrenmenschen") diese Schallenergiegröße kaum. Daher sollte man sich eher um die Schallfeldgröße, den Schallwechseldruck kümmern und um den Pegel (Schalldruckpegel SPL) als Wirkung an den Trommelfellen des Gehörs und an den Membranen der Mikrofone, sowie der entsprechenden Audiospannung bzw. seinem Spannungspegel. |
Schalldruck und Schallleistung − Wirkung und Ursache
| Die maßgebliche Größe für die Schallempfindung im Ohr ist der aus der Luftpartikelbewegung resultierende rasch veränderliche Wechseldruck der Schallwellen, der Schalldruck genannt wird. |
Umrechner: Celsius nach Fahrenheit und Fahrenheit nach Celsius
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Von Celsius nach x Grad | Von x Grad nach Celsius | |
| Fahrenheit | °F = °C × 9/5 + 32 | °C = (°F − 32) × 5/9 |
| Kelvin | K = °C + 273,15 | °C = K − 273,15 |
| Rankine | °R = (°C + 273,15) × 9/5 | °C = (°R − 491,67) × 5/9 |
| Delisle | °De = (100 − °C) × 3/2 | °C = 100 − °De × 2/3 |
| Newton | °N = °C × 33/100 | °C = °N × 100/33 |
| Réaumur | °Ré = °C × 4/5 | °C = °Ré × 5/4 |
| Rømer | °Rø = °C × 21/40 + 7,5 | °C = (°Rø − 7,5) × 40/21 |
| Von Fahrenheit nach x Grad | Von x Grad nach Fahrenheit | |
| Celsius | °C = (°F − 32) × 5/9 | °F = °C × 9/5 + 32 |
| Kelvin | K = (°F + 459,67) × 5/9 | °F = K × 9/5 − 459,67 |
| Rankine | °R = °F + 459,67 | °F = °R − 459,67 |
| Delisle | °De = (212 − °F) × 5/6 | °F = 212 − °De × 6/5 |
| Newton | °N = (°F − 32) × 11/60 | °F = °N × 60/11 + 32 |
| Réaumur | °Ré = (°F − 32) × 4/9 | °F = °Ré × 9/4 + 32 |
| Rømer | °Rø = (°F − 32) × 7/24 + 7.5 | °F = (°Rø − 7,5) × 24/7 + 32 |
|
| Die Frage nach der exakten Schallgeschwingkeit ist nicht zu beantworten. Es braucht dazu immer die Angabe der Temperatur und der Luftfeuchtigkeit, aber nicht des Luftdrucks. Die Angabe Schallgeschwindigkeit über "Meereshöhe" oder Meeresspiegel ist Unsinn, weil nur die Temperatur bedeutsam ist und nicht die Höhe über dem Meeresspiegel. |
Dichte von Wasser ρ (rho) (rein und luftfrei)
bei Normaldruck p0 = 101325 Pa.
Temperatur zwischen 0°C und 100°C
| Temperatur in °C - ρ in kg/m³ | Temperatur in °C - ρ in kg/m³ | 0 918,00 (Eis) 0 999,84 1 999,90 2 999,94 3 999,96 4 999,97 ● 5 999,96 6 999,94 7 999,90 8 999,85 9 999,78 10 999,70 11 999,60 12 999,50 13 999,38 14 999,24 15 999,10 16 998,94 17 998,77 18 998,59 19 998,40 20 998,20 21 997,99 22 997,77 23 997,54 24 997,29 25 997,04 |
26 996,78 27 996,51 28 996,23 29 995,94 30 995,64 31 995,34 32 995,02 33 994,70 34 994,37 35 994,03 36 993,68 37 993,32 38 992,96 39 992,59 40 992,21 45 990,21 50 988,03 55 985,69 60 983,19 65 980,55 70 977,76 75 974,84 80 971,79 85 968,61 90 965,30 95 961,88 100 958,35 Wasserdampf, 101325 Pa: 100 0,5 |
| Die Abhängigkeit der Wasser-Dichte vom Druck ist verhältnismäßig gering. Je 1 bar =100000 Pa Druckerhöhung erhöht sich die Dichte um etwa 0,046 kg/m³. Normale Luftdruckschwankungen haben auf die Dichte des Wassers demnach praktisch keinen Einfluss. |
| zurück |
Suchmaschine |
Startseite |