

| English version |
| Die Wellenlänge ändert sich bei Temperaturänderung der Luft, weil sich die Schallgeschwindigkeit mit der Temperatur ändert. |
|
Der Luftdruck und der Schalldruck p spielen keine Rolle, wenn es um die Wellenlänge geht. |
| Wenn bei Temperaturänderung die schwingende Luftsäule einer Flöte oder einer Orgelpfeife in der Länge konstant bleibt, dann wird die sich ändernde Schallgeschwindigkeit c die Frequenz f, also die Tonhöhe verändern. |
| Physikalische Größe | Formelzeichen | Maßeinheit | Formel |
| Frequenz | f = 1/T | Hz = 1/s | f = c / λ |
| Wellenlänge | λ | m | λ = c / f |
| Periodendauer | T = 1/f | s | T = λ / c |
| Schallgeschwindigkeit | c | m/s | c = λ · f |
| Merke: Die Schallgeschwindigkeit in Luft c = 343 m/s bei 20 °C oder die Geschwindigkeit von Radiowellen und Licht im Vakuumc = 299 792 458 m/s ≈ 300 000 km/s. Die Ausbreitungsgeschwindigkeit von elektrischen Signalen über Lichtwellenleiter liegt etwa bei 9/10 der Lichtgeschwindigkeit, das heißt ≈ 270 000 km/s. Die Ausbreitungsgeschwindigkeit von elektrischen Signalen über Kupferleitungen liegt etwa bei 2/3 der Lichtgeschwindigkeit, das heißt ≈ 200 000 km/s. |
| Interessant ist es, welche Auswirkungen die unterschiedlichen Variablen auf eine
Welle haben. Hier ist die Gleichung (Formel) einer Welle: y(t) = A · (sin ω t + φ) + C A ist die Amplitude und zeigt die halbe Differenz zwischen der oberen und unteren Auslenkung (Spitzenwert). ω ist die Winkelgeschwindigkeit: ω = 2 π f = 2 π / T Da steckt die Frequenz drin. φ ist der Phasenwinkel, der horizontale Offset. C ist der vertikale Offset auf der x-Achse, üblicherweise der DC-Offset der Welle. "Entfernung = Geschwindigkeit × Zeit" ist der Schlüssel zur grundlegenden Wellenbeziehung. |
| Eine Amplitude A (Stärke der Welle oder Lautstärke) hat absolut nichts mit der Periodendauer (Zeitdauer), der Frequenz, der Wellenlänge oder der Schallgeschwindigkeit zu tun. |
Schallgeschwindigkeit in verschiedenen Medien
| Medium | Schallgeschwindigkeit |
| PVC weich | 80 m/s |
| Luft | 343 m/s bei 20°C |
| Kork | 500 m/s |
| Helium | 1 020 m/s |
| Wasser | 1 480 m/s |
| Polystyrol | 1 800 m/s |
| Plexiglas | 1 840 m/s |
| Beton | 3 100 m/s |
| Ziegel | 3 600 m/s |
| Kiefernholz | 3 600 m/s |
| Granit | 3 950 m/s |
| Eichenholz | 4 100 m/s |
| Eisen | 5 000 m/s |
| Stahl | 5 050 m/s |
| Aluminium | 5 200 m/s |
| Quarzglas | 5 400 m/s |
| Berechnung der Schallfrequenz in Wellenlänge und zurück |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Berechnung der Radiofrequenz in Wellenlänge und zurück |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Amplitude a, Periodendauer T und Wellenlänge λ |
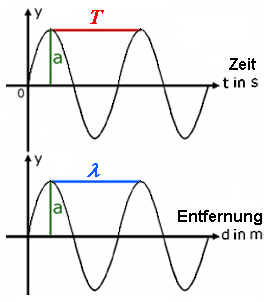 |
| y = Schalldruckp (Schalldruckamplitude). Wenn die Abbildung auf der x-Achse die Zeit t zeigt, dann sehen wir die Periodendauer T =1 / f. Wenn die Abbildung auf der x-Achse den Abstandd zeigt, dann sehen wir die Wellenlänge λ. Die größte Auslenkung oder Elongation wird mit Amplitude a bezeichnet. Frage: "Was ist eine Amplitude (Auslenkung)?"; siehe: http://www.sengpielaudio.com/Rechner-amplitude.htm Es gibt nicht nur "eine" Amplitude. Es gibt viele Amplituden; siehe: "Die Schallfeldgrößen einer ebenen Welle − Amplituden" http://www.sengpielaudio.com/SchallfeldgroessenEinerEbenenWelle.pdf" Stehende Wellen oder akustische Resonanzen haben auch mit Amplituden zu tun; siehe: http://www.sengpielaudio.com/RaummodenUndSaitenschwingungen.pdf |
Eine typische Frage: Wie ist die Beziehung zwischen Wellenlänge, Temperatur und Frequenz?
| zurück |
Suchmaschine |
Startseite |