

| English version |
| Die wahrgenommene Lautstärke ist eine psychoakustische Größe, die vom Schalldruckpegel, vom
Frequenzspektrum und dem Zeitverhalten des Schalls abhängig ist. Lautheit (engl. loudness) ist ein künstlicher Begriff aus der Psychoakustik, dem in der Umgangssprache die Lautstärke entspricht. Der Begriff Lautheit wurde erst 1936 von Stanley Smith Stevens mit dem Fachbegriff "Sone" und loudness als "Lautheit" = 40 phon bzw. 40 dB bei 1 kHz durch Psychoakustiker bei uns eingeführt; siehe: Sone und Phon. Pegel, "Volume" und Lautstärke (Lautheit): Die wahrgenommene Lautstärke oder Lautheit des Schalls ist ein komplexes Phänomen, das nicht gänzlich von Experten verstanden wird. Eine weit verbreitete Methode zur Beurteilung der Lautheit ist die SPL-Messung mit einem Schalldruckpegel- Messer, das den Schalldruckpegel in Dezibel (dB) anzeigt. Bei Audio-Produktionen wird dieses mit Pegel bezeichnet. Der Pegel eines Audiosignals ist eine Art der Messung des Lautheitseindrucks eines gehörten Signals und ist ein Teil der Information, die in einer Audio-Datei gespeichert ist. |
| Vermeide die Verwendung der psychoakustischen Ausdrücke Lautstärke und Lautheit. Diese subjektive Schall-Empfindung ist nicht eindeutig messbar. Die Begriffe "Lautstärke" oder "Lautheit" sind ein Problem, weil diese zur Psycho-Akustik gehören und solch eine persönliche Empfindung nicht klar bestimmbar ist. Lautheit oder Lautstärke wird als psychologische Ergänzung der physischen Schall- Stärke (Amplitude) auch nach anderen Parametern als dem Schalldruck beurteilt, einschließlich der Frequenz, der Bandbreite, der spektralen Zusammensetzung, dem Informationsgehalt, der zeitlichen Struktur, der subjektiven Einstellung, sowie der Einwirkungsdauer des Schallsignals. Der gleiche Schall erzeugt nicht bei allen Individuen (Menschen) die gleiche Lautheitsempfindung. |
| Als psychoakustische Größen zur Beschreibung der "Lautstärke" gibt es den "Lautstärkepegel" (Lautheitspegel) LN mit der Einheit Phon und die "Lautheit" N mit der Einheit Sone. |
| Der Lautstärke- Knopf. Gain und Volume. |
 |
Lautstärke- Pegel ändern. Pegel und Lautheit. |
| Beim Begriff Faktor (Ratio, Gain) ist immer anzugeben, ob die Energiegröße, die Feldgröße (Amplitude) oder die psychoakustische Lautheitsgröße gemeint ist. |
Umrechnung: Faktor, Ratio, Gain (Verstärkung) in
Pegeländerung (Gain Dezibel dB) und zurück
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Energiegröße x ist Feldgröße y (Amplitude RMS) quadriert: x ~ y2.
Zwei Autos. Wie laut?
| Eine gute Anfrage: "Sind zwei Autos doppelt so laut wie
ein Auto? Und wenn nicht, um welchen Faktor sind denn
zwei Autos lauter als ein Auto?" Die Addition zweier pegelgleicher Schallquellen ergibt eine Anhebung des Schallpegels von (+)3 dB − Das entspricht einem Schalldruck-Faktor (Amplitude) von 1,414; siehe: Pegeladdition zweier gleichlauter unkorrelierter akustischer Schallquellen
Der obige Rechner bringt als "Faktor" folgende Ergebnisse: 1. Die Pegeländerung Δ Llaut = 3 dB zeigt als psychoakustische Größe den Faktor der empfundenen Lautheit (Lautstärke) z = 1,232. 2. Die Pegeländerung Δ Lp = 3 dB zeigt als Feldgröße den Faktor der gemessenen Spannung, (Schalldruck) y = 1,414. 3. Die Pegeländerung Δ LI = 3 dB zeigt als Energiegröße den Faktor der berechneten Energie (Leistung) x = 2. Man erkennt, dass es beim Schall 3 unterschiedliche Faktoren gibt, die penibel auseinander gehalten werden müssen. Welcher Faktor ist denn gefordert? Die Lautstärke als Empfindung, der Schalldruck als Messung oder die Schallintensität als Berechnung? Die typische Frage ist doch: Ein "Schall" soll verdoppelt werden. Wieviel mal mehr ist denn das? Soll die Dezibel-Zahl verdoppelt werden? Muss der Schalldruck in Pascal verdoppelt werden? Soll die Schallintensität in Watt pro Quadratmeter (W/m2) verdoppelt werden? Muss die psychoakustisch empfundene Lautstärke (Lautheit) verdoppelt werden? Na? Das ist den Fragenden eigentlich nie richtig klar. Was ist Schall? Weitere Fragen: Verdoppeln des Schalls bzw. des Schallpegels? |
Pegel in Dezibel (dB) und ihre unterschiedlichen Faktoren
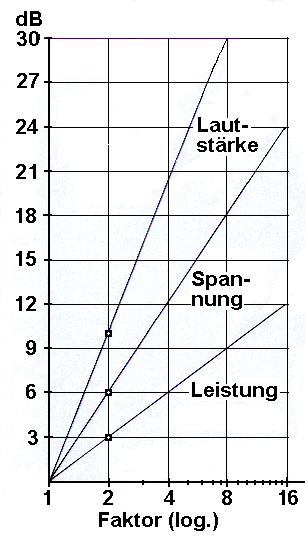 |
| Doppelte Lautheit = Faktor 2 ist 10 dB mehr empfundener Lautstärkepegel (Psychoakustik) Doppelte Spannung = Faktor 2 ist 6 dB mehr gemessener Spannungspegel (Schalldruckpegel) ● Doppelte Leistung = Faktor 2 ist 3 dB mehr berechneter Leistungspegel (Schallintensitätspegel) |
| Während 6 dB SPL eine Verdopplung der Amplitude darstellt, ist eine nicht exakte Daumen-Regel, dass jede 10-dB-Erhöhung eine Verdoppelung der wahrgenommenen Lautstärke darstellen soll - sagen uns die Psycho-Akustiker. |
Faktor |
Energiegröße |
Feldgröße |
Empfindungsgröße |
Verhältnis (Ratio) |
Energiepegel (Leistung) |
Spannungspegel |
Lautstärkepegel |
| 16 | +12 | +24 | +40 |
| 10 | +10 | +20 | +33.22 |
| 8 | +9 | +18 | +30 |
| 4 | +6 | +12 | +20 |
| √10 = 3.16 | +5 | +10 | +16.6 |
| 3 | +4.77 | +9.54 | +15.85 |
| 2 | +3 | +6 | +10 |
| 1.516 | +1.81 | +3.62 | +6 |
| √2 = 1.414 | +1.5 | +3 | +5 |
1.232 |
+0.9 | +1.8 | +3 |
| 1 | ±0 | ±0 | ±0 |
| 0.812 | −0.9 | −1.8 | −3 |
| 0.707 | −1.5 | −3 | −5 |
| 0.660 | −1.81 | −3.62 | −6 |
| 1/2 = 0.500 | −3 | −6 | −10 |
| 1/3 = 0.333 | −4.77 | −9.54 | −15.85 |
| 1/√10 = 0.316 | −5 | −10 | −16.6 |
| 1/4 = 0.25 | −6 | −12 | −20 |
| 1/8 = 0.125 | −9 | −18 | −30 |
| 1/10 = 0.1 | −10 | −20 | −33.22 |
| 1/16 = 0.0625 | −12 | −24 | −40 |
V2/V1 = 10(GV in dB/20) | GP = 10·log (P2/P1) |
GV = 20·log (V2/V1) |
GL = 33.22·log (x) |
![]()
 |
|
||||||||||||||||||||||||||||||
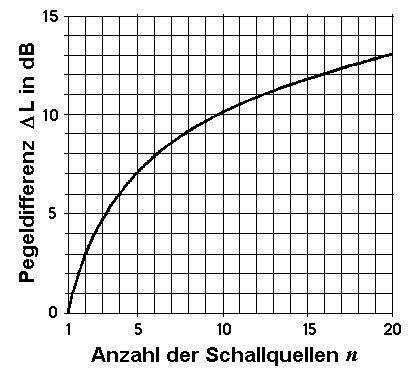
| Mehrere gleich starke Schallquellen erzeugen an einem bestimmten Ort einen Schalldruck, bzw. einen Schalldruckpegel. Bei der Addition solcher inkohärenter Quellen vereinfacht sich die Gleichung zur Berechnung des Summenschalldruckpegels wie folgt: |
Formeln: Δ L = 10 · log n oder n = 10(ΔL/10)
Δ L = Pegelzunahme; n = Anzahl der gleich lauten Schallquellen.
| Für n = 2 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 2 = +3,01 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 3 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 3 = +4,77 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 4 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 4 = +6,02 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 10 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 10 = +10,00 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. |
![]()
Pegelzunahme bei gleichstarken inkohärenten Schallquellen
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Der Gesamtpegel in dB ergibt sich aus dem Pegel einer Schallquelle,
zu dem die Pegelzunahme (der Pegelzuwachs) linear addiert wird.
![]()
Lautstärke - Schalldruck - Intensität
Faktoren und ihre Pegel in Dezibel (dB)
Lautstärke Empfindung - Schalldruck Effekt - Schallintensität Ursache
|
| Aus: http://www.bv-elbtal.de/html/was_ist_larm_.html |
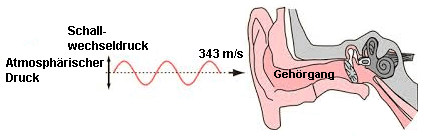
Schallwellen bewegen unsere Trommelfelle.
Aber welche Schallgröße erzeugt denn diese Wirkung?
 |
|
Schalldruck und Schallleistung – Wirkung (Effekt) und Ursache Schallleistung ist zwar die Ursache - aber Schalldruck erzeugt die hörbare Wirkung (Effekt). |
| Gain/Loss als Ratio Faktor (out/in) |
Gain/Loss als Faktor |
Gain/Loss in dB Energiegröße (Power gain) |
Gain/Loss in dB Feldgröße (Voltage gain) |
Gain/Loss in dB Psychogröße (Loudness gain) |
| 1000:1 | 1000 | +30,00 dB | +60,00 dB | +99,66 dB |
| 100:1 | 100 | +20,00 dB | +40,00 dB | +66,44 dB |
| 10:1 | 10 | +10,00 dB | +20,00 dB | +33,22 dB |
| 5:1 | 5 | +6,99 dB | +13,98 dB | +23,22 dB |
| 4:1 | 4 | +6,02 dB | +12,04 dB | +20,00 dB |
| 2:1 | 2 | +3,01 dB ● | +6,02 dB ● | +10,00 dB ● |
| 1:1 | 1 | 0,00 dB | 0,00 dB | 0,00 dB |
| 1:2 | 0.5 | −3,01 dB ● | −6,02 dB ● | −10,00 dB ● |
| 1:4 | 0,25 | −6,02 dB | −12,04 dB | −20,00 dB |
| 1:5 | 0,2 | −6,99 dB | −13,98 dB | −23,22 dB |
| 1:10 | 0,1 | −10,00 dB | −20,00 dB | −33,22 dB |
| 1:100 | 0,01 | −20,00 dB | −40,00 dB | −66,44 dB |
| 1:1000 | 0,001 | −30,00 dB | −60.00 dB | −99,66 dB |
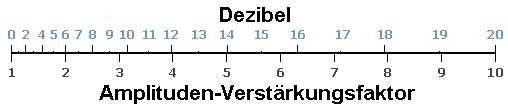
| 20 dB Lautheitsverstärkung (Empfindung) ist 4 Mal der Lautheits-Verstärkungsfaktor. 20 dB Spannungsverstärkung (Amplitude) ist 10 Mal der Spannungs-Verstärkungsfaktor. 20 dB Leistungsverstärkung (Energie) ist 100 Mal der Leistungs-Verstärkungsfaktor. |
Schallpegel-Vergleichstabelle und der Faktor
| Die Schallpegelabhängigkeit und die dazugehörende Änderung des Faktors bei subjektiver
Lautstärke (Lautheit) und objektivem Schalldruck (Spannung) und Schallintensität (Leistung). Wieviel Dezibel (dB) Pegeländerung ist zweimal, halb oder viermal so laut? Wieviel dB erscheinen doppelt so laut zu sein? Hier folgen die diversen Faktoren. |
| Pegel- Änderung |
Lautstärke Lautheit |
Spannung Schalldruck |
Schallleistung Schallintensität |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31,6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2,0 = Verdopplung | 3,16 = √10 | 10 |
| +6 dB | 1,52-fach | 2,0 = Verdopplung | 4,0 |
| +3 dB | 1,23-fach | 1,414-fach = √2 | 2,0 = Verdopplung |
| - - - - ±0 dB - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - |
| −3 dB | 0,816-fach | 0,707-fach | 0,5 = Halbierung |
| −6 dB | 0,660-fach | 0,5 = Halbierung | 0,25 |
| −10 dB | 0,5 = Halbierung | 0,316 | 0,1 |
| −20 dB | 0,25 | 0,100 | 0,01 |
| −30 dB | 0,125 | 0,0316 | 0,001 |
| −40 dB | 0,0625 | 0,0100 | 0,0001 |
| Log. Größe | Psychogröße | Feldgröße | Energiegröße |
| dB- Änderung |
Lautstärke- faktor |
Amplituden- faktor |
Leistungs- faktor |
| Merke: Für eine Pegeländerung von 10 dB brauchen wir zehnmal mehr Leistung vom Verstärker. Diese Erhöhung des Schallpegels bedeutet eine Erhöhung des Schalldrucks um den Faktor 3,16. Die psycho-akustische Lautstärke bzw. Lautheit ist dagegen eine subjektive Empfindungsgröße. |
|
Der Pegel der Ausgangsleistung ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 50% (Faktor = 0.5) und der Pegel von −6 dB ist entsprechend 25% (= 1/4 = 0,25) der ursprünglichen Leistung. Dieses gilt für die Energiegröße Leistung bzw. Schalllintensität. Der Pegel der Ausgangsspannung ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 70,7% (Faktor = 0,7071), und der Pegel von −6 dB ist entsprechend 50% (= 1/2 = 0,5)der ursprünglichen Spannung. Dieses gilt für die Feldgröße Spannung bzw. Schalldruck. Der Pegel der Ausgangslautstärke ist 0 dB, also 100% (Faktor oder Verhältnis = 1). Der Pegel von −3 dB entspricht 81,2% (Faktor = 0,812), und der Pegel von −6 dB ist entsprechend 66% (Faktor = 2/3 = 0,66) der ursprünglichen Lautheit. Dieses gilt für die Lautheitsgröße Lautheit bzw. Lautstärkepegel. |
 |
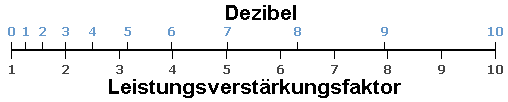 |
| Eine typische Frage: "16 dB sind wieviel Mal?" Antwort: Ist eine Feldgröße, wie Schalldruck oder ist eine Energiegröße, wie Schallintensität gemeint? Deswegen gibt der Rechner zwei Antworten: Der Faktor ist: 6,31 oder der Faktor ist: 39,8; je nachdem, ob eine Feldgröße oder eine Energiegröße gemeint ist. 6,312 (Feldgröße zum Quadrat) = 39,8 (Energiegröße). |
| Fragen: Für einen Verstärker mit einer 100-fachen Spannungsverstärkung, berechne man das Folgende: a) Verstärkungspegel (Gain) in dB. b) Verstärkungspegel (Gain) bei der Grenzfrequenz in dB. c) Spannungsverstärkung bei der Grenzfrequenz. Antworten: a) Spannungsverstärkung 100 ≡ 40 dB Voltage Gain b) Bei der Grenzfrequenz gibt es 3 dB weniger Gain − also 37 dB. c) Voltage Gain 37 dB ≡ 70,7-fache Spannungsverstärkung. |
| back |
Search Engine |
home |