Berechnung: Leistung, Spannung, Verstärkung, Dämpfung berechnen Rechner - sengpielaudio
 
English version UK-flag - sengpielaudio D-flag - sengpielaudio
 
Berechnen:
● Spannungsverstärkung und Leistungsverstärkung ●
• Spannungsdämpfung und Leistungsdämpfung •
 
Eine provokante Frage: Kann man überhaupt Leistung verstärken? Elektrische Spannung und
elektrischen Stom kann man verstärken. Energie lässt sich in verschiedene Energieformen
umwandeln. Beim Energiesparen möchte man mit weniger Energie mehr Leistung erzeugen.
Die Bezeichnung "Verstärker" verschleiert, dass die Energie durchweg aus dem Stromnetz kommt und größtenteils
auch wieder als Verlust die Geräte verlässt. Man kann wegen der Energieerhaltung nicht aus einer kleinen Leistung
eine große machen. Jedoch kann man immerhin die Daten vom schwachen Strom auf den starken übertragen.

Finde die Spannungsverstärkung oder Spannungsdämpfung und das Verhältnis Eingang zu Ausgang,
wenn die Eingangsspannung und Ausgangsspannung gegeben ist

   Eingangsspannung  Volt
  Ausgangsspannung  Volt
 Spannungs-Verstärkung/Dämpfung  dB
                    Ratio Eingang/Ausgang      
     
 

Finde die Leistungsverstärkung oder Leistungsdämpfung und das Verhältnis Eingang zu Ausgang,
wenn die Eingangsleistung und die Ausgangsleistung eingegeben wird:
 
Merke: Power gain wird in der Audiotechnik (Tontechnik) nicht verwendet.

       Leistung vorher  Watt
   Leistung hinterher  Watt
  Leistungs-Verstärkung/Dämpfung  dB  
              Ratio Eingang/Ausgang     
     

Finde die Ausgangsspannung, wenn die Eingangsspannung und die
Spannungsverstärkung oder die Spannungsdämpfung in dB eingegeben wird:

                              Eingangsspannung  Volt 
Spannungs-Verstärkung/Dämpfung  dB
Ausgangsspannung  Volt
     

Finde die Ausleistung, wenn die Eingangsleistung und die
Leistungssverstärkung oder die Leistungsdämpfung in dB eingegeben wird:
 
Merke: Power gain wird in der Audiotechnik (Tontechnik) nicht verwendet.

                                Eingangsleistung  Watt 
Leistungs-Verstärkung/Dämpfung  dB
Ausgangsleistung  Watt
    
Spannungsverhältnis und Spannungspegel Formel Spannungspegel

Leistungsverhältnis und Leistungspegel Formel Leistungspegel
  Not used in Audio

Einfach den Wert links oder rechts eingeben.
Der Rechner arbeitet in beide Richtungen des ↔ Zeichens.
Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Verstärkungsfaktor v = U2/U1
für die Feldgröße Spannung
  ↔  Verstärkungsmaß L
Spannungspegel
dB
FormelVerstaerkungsfaktor    v = U2 / U1   Formel Verstaerkung
Spannungspegel 0 dB entspricht der Spannungsverstärkung v = 1

In der Tontechnik ist "Leistungsverstärkung" nicht üblich; selbst
Leistungsverstärker für Lautsprecher verstärken keine Leistung.
Sie verstärken die Audio-Spannung, welche die Schwingspule bewegt.

Verstärkungfaktor v = P2/P1
für die Energiegröße Leistung
  ↔  Verstärkungsmaß L
Leistungspegel
dB
Start    v = P2 / P1   Start
Leistungsspegel 0 dB entspricht der Leistungsverstärkung v = 1
 
Leistung, ist wie alle Energiegrößen
überwiegend eine berechnete Größe.
 

Aha!
 
Die in dB ausgedrückte Spannungsverstärkung ist bei der Grenzfrequenz um
20 · log10 (1/√2) ≈ (−)3,0103 dB kleiner als die maximale Spannungsverstärkung.
Das entspricht einem Faktor von 0,7071 oder 70,71%.
 
Die in dB ausgedrückte Leistungsverstärkung ist bei der Grenzfrequenz um
10 · log10 (½) ≈ (−)3,0103 dB kleiner als die maximale Leistungsverstärkung.
Das entspricht einem Faktor von 0,5 oder 50%.
 

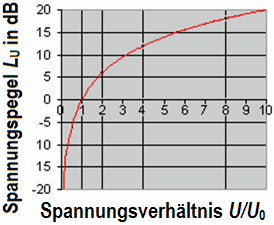
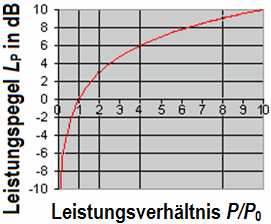
Dezibel sind als das Zehnfache des log eines "Leistungsverhältnis" definiert. Dezibel konvertieren Multiplikation und Division Berechnungen in einfache Additionen und Subtraktionen. Jedoch verwenden wir in der Audiotechnik nie das Leistungsverhältnis. Wir mögen die Spannung, den Schalldruck oder die Amplitude. Für uns ist Dezibel als das zwanzigfache vom Logarithmus eines Amplitudenverhältnisses definiert.
 
Ratio
(OUT / IN)		 Voltage Gain
(dB)		 "Power Gain"
(dB)
   1/1000    −60    −30
   1/100    −40    −20
   1/10    −20    −10
   1/5    −14    −7
   1/2    −6.02    −3.01
     1      0      0
     2    +6.02    +3.01
     5    +14    +7
   10    +20    +10
   100    +40    +20
   1000    +60    +30
 
Spannungsverstärkung Voltage Gain   Leistungsverstärkung Power Gain
Spannungsverhältnis
Faktor U2/U1		 Spannungsverstärkung
GV in dB		   Leistungsverhältnis
Faktor P2/P1		 Leistungsverstärkung
GP in dB
103 +60     106 +60  
102 +40     104 +40  
101 +20     102 +20  
√10 = 3,16 +10     10  +10  
2 +6   4 +6
√2 = 1,414 +3   2 +3
1 ±0   1 ±0
1/√2 = 0,7071 −3   1/2 = 0,5 −3
1/2 = 0,5 −6     1/4 = 0,25 −6
1/√10 = 0,316 −10     10−1 = 0,1  −10  
10−1 = 0,1   −20     10−2 = 0,01 −20  
10−2 = 0,01 −40     10−4 = 0,0001 −40  
  10−3 = 0,001 −60     10−6 = 0,000001 −60  
V2/V1 = 10(GV in dB/20) GV = 20·log (V2/V1)   P2/P1 = 10(GP in dB/10) GP = 10·log (P2/P1)
 
Spannungsverstärkung (gain in dB) = 20·log (Audio Ausgangsspannung / Audio Eingangsspannung) - wird verwendet in der Audio-Technik.
Spannungsverstärkung ist definiert als Ratio der Ausgangsspannung zur Eingangsspannung in dB. Angenommen die Eingangsspannung sei 10 mV (+10 dBu) und die Ausgangsspannung ist 1 V (1000 mV, +60 dBm). Das Verhältnis (ratio) ist 1000/10 = 100 und die Spannung (gain) ist:
20·log 100 = 40 dB. Bezugsspannung V0 = 1 Volt.
 
Leistungsverstärkung (gain dB) = 10·log (HF Ausgangsleistung / HF Eingangsleistung) - wird verwendet in der HF-Technik.
Leistungsverstärkung ist definiert als Ratio der Ausgangsleistung zur Eingangsleistung in dB.
Angenommen die Eingangsleistung sei 10 mW (+10 dBm) und die Ausgangsleistung ist 1 W
(1000 mW, +30 dBm). Das Verhältnis (ratio) ist 1000/10 = 100 und die Leistung (gain) ist:
10·log 100 = 20 dB. Bezugsleistung P0 = 1 Watt.
 
 
 
zurück zurueck Suchmaschine weiter Startseite Start