

| English version |
| Dezibel sind logarithmische "Einheiten", die nicht wie andere Zahlen linear addiert werden dürfen. In den meisten Fällen addieren wir unkorrelierte Signale als Geräusch oder als Musik. Erzeugt eine Schallquelle einen Schallpegel (Schalldruckpegel SPL) von L1 = 60 dB und eine andere Schallquelle kommt mit L2 = 60 dB hinzu, dann ergeben die beiden inkohärenten Signale keinen Pegel von 120 dB, sondern einen Gesamt-Pegel von 63 dB. Wenn beide Werte gleich sind, so ist das noch einfach. Anders sieht es aus, wenn beide elektrisch oder akustisch zusammengeführten inkohärenten Pegel unterschiedlich groß sind. Mehr als 3 dB größer als der höhere der beiden inkohärenten Pegel kann der Summenpegel niemals werden. Unter Superposition (lat. super = über; positio = Lage, Setzung, Stellung) versteht man generell eine Überlagerung. Hier überlagern sich zwei Schallquellen. Siehe auch den anderen Fall: ● Addition von elektrischen kohärenten Signalen. |
Addition von Amplituden (und Pegeln)
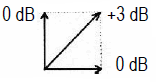 |
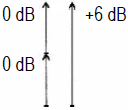 |
|
| Leistungssumme inkohärent (90°) √ (1² + 1²) = 1,414... |
Spannungssumme kohärent (0°) 1 + 1 = 2 |
| Die Addition zweier inkohärenter Schalldruck- oder Spannungspegel ist: Die Addition zweier pegelgleicher Werte ergibt eine Anhebung des Gesamtpegels von (+)3 dB. Diese Gleichung wird sowohl für die elektrische Addition inkohärenter Signale, als auch für die Berechnung des Energiepegels zweier Lautsprecher verwendet. Die Addition zweier kohärenter Schalldruck- oder Spannungspegel ist: Die Addition zweier pegelgleicher Werte ergibt hier eine Anhebung des Gesamtpegels von (+)6 dB. Dieses erhält man bei gleicher Ansteuerung von zwei dicht nebeneinander stehenden Lautsprechern. |
Pegeldifferenz in dB der zu addierenden Pegel Die zum höheren Pegel zu addierende Pegeldifferenz |
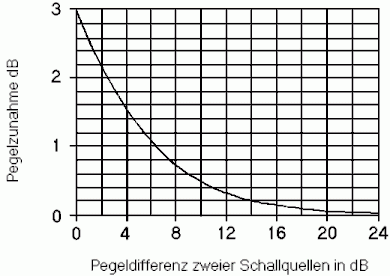 |
| Für den Summenschallpegel von n inkohärent abstrahlenden Quellen gilt 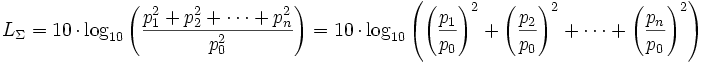 p0 ist der Bezugswert (Referenz) des Schalldrucks. Hörschwelle bei 1 kHz. = 0.00002 Pa = 20 µPa. |
Pegeladdition mehrerer inkohärenter Schallquellen
![]()
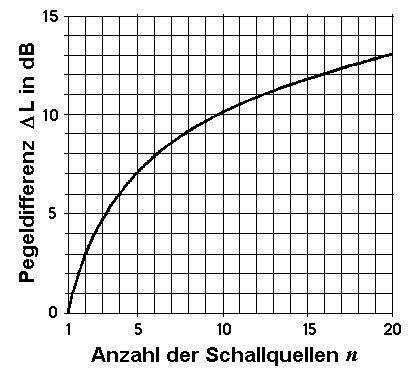
Addieren von gleich starken inkohärenten Schallsignalen
 |
|
||||||||||||||||||||||||||||||
| Mehrere gleich starke Schallquellen erzeugen an einem bestimmten Ort einen Schalldruck, bzw. einen Schalldruckpegel. Bei der Addition solcher inkohärenter Quellen vereinfacht sich die Gleichung zur Berechnung des Summenschalldruckpegels wie folgt: |
Formeln: Δ L = 10 × log n oder n = 10(ΔL/10)
Δ L = Pegelzunahme; n = Anzahl der gleich lauten Schallquellen.
| Für n = 2 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 2 = +3,01 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 3 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 3 = +4,77 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 4 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 4 = +6,02 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 10 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 10 = +10,00 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. |
Pegelzunahme bei gleichstarken inkohärenten Schallquellen
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Der Gesamtpegel in dB ergibt sich aus dem Pegel einer Schallquelle,
zu dem die Pegelzunahme (der Pegelzuwachs) linear addiert wird.
![]()
Was ist denn Schallpegel?
Eine Reduktion des Schallleistungspegels der Schallquelle um 6 dB führt zu einer Reduktion des
Schalldruckpegels und des Schallintensitätspegels am Ort des Empfängers von ebenfalls 6 dB, auch
wenn die Schallleistung selbst auf den Faktor 0,25 – der Schalldruck aber auf den Faktor 0,5 und die
Schallintensität auf den Faktor 0,25 abgefallen ist. Der Referenzwert (Bezugswert) für den Schallpegel
wurde so gewählt, dass sich bei einer Schallkennimpedanz von Z0 = ρ · c = 400 N·s/m3 für den
Schallintensitätspegel der gleiche Wert ergibt wie für den Schalldruckpegel. Wir sprechen daher einfach
vom "Schallpegel" und lassen offen, ob Schalldruckpegel oder Schallintensitätspegel gemeint ist.
|
| zurück |
Suchmaschine |
Startseite |