

| Deutsche Version |
| Perceived loudness is a psycho-acoustic quantity that depends on
sound pressure level, the frequency spectrum, and the time behavior of the sound in question. Level, Volume, and Loudness: The sone is a unit of perceived loudness proposed by Stanley Smith Stevens in 1936. That is: 40 phon or 40 dB at 1 kHz; see: Sone and phon. Perceived volume or loudness of sound, is a complex phenomenon, not entirely understood by experts. One widely-agreed method of assessing loudness is by measuring SPL with a sound pressure level meter, which is the sound pressure level in decibels (dB). In audio production communities, this is called level. The level of an audio signal is one way of measuring the signal's perceived loudness, and is part of the information stored in an audio file. |
| Avoid using the psychoacoustical terms loudness perception and volume. This subjective sound-sensation is not clearly measurable without ambiguity. The term "loudness" or "volume" is a problem because it belongs to psycho- acoustics and this personal feeling is not correct definable. Loudness as a psychological correlate of physical strength (amplitude) is also affected by parameters other than sound pressure, including frequency, bandwidth, spectral composition, information content, time structure, and the duration of exposure of the sound signal. The same sound will not create the same loudness perception by all individuals (people). |
| As psycho-acoustic parameters to describe the "loudness" there is the "loudness level" LN with the unit phon and the "loudness" N with the unit sone. |
| The volume knob. Gain and volume |
 |
Change the loudness level. Level and loudness |
| Using the terms "ratio" or "gain", you can indicate if energy quantity (power), field quantity (amplitude) or psychoacoustic loudness quantity is the intended meaning. |
Conversion: Factor, ratio, gain to
Level value (Decibel dB Gain) and vice versa
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
Energy quantity x is field quantity y (amplitude rms) squared: x ~ y2.
Two cars. How loud?
| A good question: "Are two cars twice as loud as one car? And if not, by what factor are two cars louder than one car?" The addition of two identical sound sources results in an increased of the sound level of (+)3 dB - That equals a sound pressure factor (amplitude) of 1.414; see: Total level adding of two equal loud non-coherent acoustical sound sources
The above calculator gives the following results for the factors: 1. The level change Δ Lloud = 3 dB shows as psychoacoustic quantity the factor of the perceived psychoacoustic loudness (volume) z = 1.232. 2. The level change Δ Lp = 3 dB shows as field quantity the factor of measured the voltage (sound pressure) y = 1.414. 3. The level change Δ LI = 3 dB shows as energy quantity the calculated factor of the energy (power) x = 2. It is apparent that for sound, there are three different factors that must be kept scrupulously apart. Which factor is required? The loudness as sensation (feeling), the sound pressure as measuring, or the sound intensity as calulation? The typical question is: A "sound" has to be doubled. How many more times is this? Should the decibel value of the soundbe doubled? Need the sound pressure in pascals be doubled? Should the sound intensity in watts per square meter (W/m2) bedoubled? Need the psycho-acoustically perceived loudness be doubled? Well? Actually this is never clear for the questioner. What is sound? More questions: How much is doubling of noise levels? Doubling of sound levels? |
Levels in decibels (dB) and their different factors
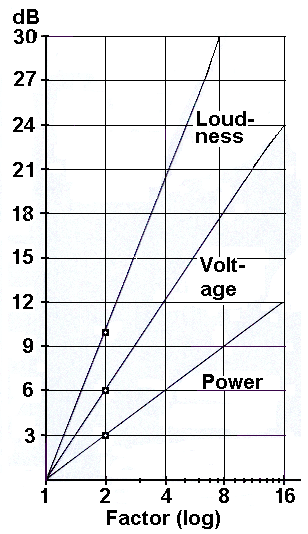 |
| Double or twice the loudness = factor 2 means 10 dB more sensed loudness level (psycho acoustic) Double or twice the voltage = factor 2 means 6 dB more measured voltage level (sound pressure level) ● Double or twice the power = factor 2 means 3 dB more calculated power level (sound intensity level) |
| While every 6 dB SPL represents a doubling of amplitude, a non-exact rule-of-thumb is that every 10 dB increase is a doubling of perceived loudness - psycho-acousticians tell us. |
| Factor | Energy quantity | Field quantity | Perception quantity |
| Ratio P2/P1 V2/V1 L2/L1 |
Power, Energy Gain GP in dB |
Voltage Gain GV in dB |
Loudness Gain GL in dB |
| 16 | +12 | +24 | +40 |
| 10 | +10 | +20 | +33.22 |
| 8 | +9 | +18 | +30 |
| 4 | +6 | +12 | +20 |
| √10 = 3.16 | +5 | +10 | +16.6 |
| 3 | +4.77 | +9.54 | +15.85 |
| 2 | +3 | +6 | +10 |
| 1.516 | +1.81 | +3.62 | +6 |
| √2 = 1.414 | +1.5 | +3 | +5 |
| 1.232 | +0.9 | +1.8 | +3 |
| 1 | ±0 | ±0 | ±0 |
| 0.812 | −0.9 | −1.8 | −3 |
| 0.707 | −1.5 | −3 | −5 |
| 0.660 | −1.81 | −3.62 | −6 |
| 1/2 = 0.500 | −3 | −6 | −10 |
| 1/3 = 0.333 | −4.77 | −9.54 | −15.85 |
| 1/√10 = 0.316 | −5 | −10 | −16.6 |
| 1/4 = 0.25 | −6 | −12 | −20 |
| 1/8 = 0.125 | −9 | −18 | −30 |
| 1/10 = 0.1 | −10 | −20 | −33.22 |
| 1/16 = 0.0625 | −12 | −24 | −40 |
| V2/V1 = 10(GV in dB/20) | GP = 10×log (P2/P1) | GV = 20×log (V2/V1) | GL = 33.22×log (x) |
![]()
Adding of equal loud non-coherent sound sources
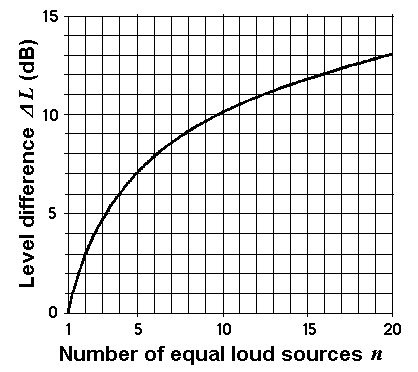 |
|
||||||||||||||||||||||||||||||
Formulas: Δ L = 10 × log n or n = 10(ΔL/10)
Δ L = level difference; n = number of equal loud sound sources.
| n = 2 equally loud non-coherent sound sources result in a higher level of 10 × log10 2 = +3.01 dB compared to the case that only one source is available. n = 3 equally loud non-coherent sound sources result in a higher level of 10 × log10 3 = +4.77 dB compared to the case that only one source is available. n = 4 equally loud non-coherent sound sources result in a higher level of 10 × log10 4 = +6.02 dB compared to the case that only one source is available. n =10 equally loud non-coherent sound sources result in a higher level of 10 × log10 10 = +10.00 dB compared to the case that only one source is available. |
Adding (combining) levels of equal loud sound sources
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
The total level in dB is the level of one sound source plus the increase of level in dB.
![]()
Sound loudness - Sound pressure - Sound intensity
Factors and their levels in decibels (dB)
Loudness perception - sound pressure effect - sound intensity cause
|
|
Sound waves move our eardrums (tympanic membranes).
But which sound quantity produces this effect?
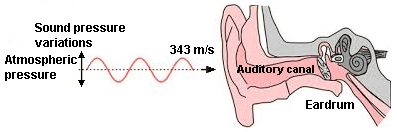 |
|
Sound pressure and Sound power – Effect and Cause Sound power is the cause - but sound pressure produces the audible effect. |
| Gain/loss as a ratio factor (out/in) |
Gain/loss as a factor |
Gain/loss in dB Energy quantity (Power gain) |
Gain/loss in dB Field quantity (Voltage gain) |
Gain/loss in dB Psycho quantity (Loudness gain) |
| 1000:1 | 1000 | +30.00 dB | +60.00 dB | +99.66 dB |
| 100:1 | 100 | +20.00 dB | +40.00 dB | +66.44 dB |
| 10:1 | 10 | +10.00 dB | +20.00 dB | +33.22 dB |
| 5:1 | 5 | +6.99 dB | +13.98 dB | +23.22 dB |
| 4:1 | 4 | +6.02 dB | +12.04 dB | +20.00 dB |
| 2:1 | 2 | +3.01 dB ● | +6.02 dB ● | +10.00 dB ● |
| 1:1 | 1 | 0.00 dB | 0.00 dB | 0.00 dB |
| 1:2 | 0.5 | −3.01 dB ● | −6.02 dB ● | −10.00 dB ● |
| 1:4 | 0.25 | −6.02 dB | −12.04 dB | −20.00 dB |
| 1:5 | 0.2 | −6.99 dB | −13.98 dB | −23.22 dB |
| 1:10 | 0.1 | −10.00 dB | −20.00 dB | −33.22 dB |
| 1:100 | 0.01 | −20.00 dB | −40.00 dB | −66.44 dB |
| 1:1000 | 0.001 | −30.00 dB | −60.00 dB | −99.66 dB |
| 20 dB loudness reinforcement (sensation) is 4 times the loudness factor. 20 dB voltage gain (amplitude) is 10 times the voltagefactor. 20 dB power gain (energy) is 100 times the power factor |
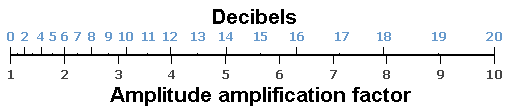
Sound Level Comparison Chart and the Ratios
| Table of sound level dependence and the change of the respective ratio to subjective
volume (loudness), objective sound pressure (voltage), and sound intensity (acoustic power). How many decibels (dB) level change is double, half, or four times as loud? How many dB to appear twice as loud (two times)? Here are all the different ratios. Ratio means "how many times" or "how much" ... Doubling of loudness. |
| Level Change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31.6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 0.25 | 0.100 | 0.01 |
| −30 dB | 0.125 | 0.0316 | 0.001 |
| −40 dB | 0.0625 | 0.0100 | 0.0001 |
| Log. size | Psycho size | Field size | Energy size |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
| For a 10 dB increase of the level, we require ten times more power from the amplifier. For a 10 dB increase of the level, we require 3.16 times more voltage from the amplifier. Loudness and volume are highly subjective. That belongs to the domain of psychoacoustics. |
| The level of the output power level is 0 dB, that is 100% (factor or ratio = 1). The level of −3 dB is equivalent to 50% (factor = 0.5) and the level of −6 dB is equivalent to 25% (factor = 1/4 = 0.25) of the initial power. This applies to the energy quantity power or sound intensity. The level of the output voltage level is 0 dB, that is 100% (factor or ratio = 1). The level of −3 dB is equivalent to 70.7% (factor = 0.7071), and the level of −6 dB is equivalent to 50% (factor = 1/2 = 0.5) of the initial voltage. This applies to the field quantity voltage or sound pressure. The level of the output loudness level is 0 dB, that is 100% (factor or ratio = 1). The level of −3 dB is equivalent to 81.2% (factor = 0.812), and the level of −6 dB is equivalent to 66% (factor = 2/3 = 0.66) of the initial loudness. This applies to the loudness quantity. Loudness or loudness level (volume). |
 |
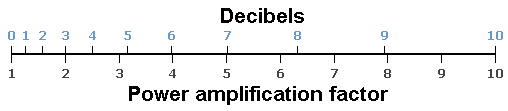 |
| A typical question: "16 dB how many times?" Answer: Do they mean a field quantity, like a sound pressure or an energy quantity, like a sound intensity? That is why the calculator gives two answers: The factor is: 6.31 or the factor is: 39.8 depending on field quantity or energy quantity. 6.312 (field quantity squared) = 39.8 (energy quantity). |
| Questions: For an amplifier with an amplification factor of 100, calculate the following: a) voltage gain in dB. b) voltage gain at the cutoff frequency (break frequency) in dB. c) amplification factor at the cutoff frequency (break frequency). Answers: a) amplification factor 100 ≡ voltage gain 40 dB b) gain at the cutoff frequency is 3 dB less − so it is 37 dB. c) voltage gain 37 dB ≡ amplification factor 70.7 at the cutoff frequency. |
| back |
Search Engine |
home |