Decibel dB calculation amplification factor gain loss and damping factor ratio voltage power - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
● Calculation: Amplification (gain) and damping (loss)
as factor ( ratio) to the level in decibels (dB) ●
 
Gain is the ratio between the magnitude of output and input signals.
Gain controls on an amplifier are basically just small potentiometers (variable
resistors) or volume controls, that allow you to adjust the incoming signal to the
amplifier.
 
The amplification factor, also called gain, is the extent to which a device boosts the strength of a signal.
The damping factor, also called loss, is the extent to which a device reduces the strength of a signal.
 
Enter two values and press the right calculate bar in the line of the missing answer

 
Input: voltage power
 
Input   value 1
Output   value 2
 Level change   dB
 
In analog audio engineering we deal only with 'voltage' amplification (gain) and damping (loss).
gain and loss
V1 = Vin and V2 = Vout
V2 > V1 or Vout > Vin means amplification. The dB value is positive (+).
V2 < V1 or Vout < Vin means damping. The dB value is negative (−).
V2 / V1 or Vout / Vin means the ratio. The amplification or the damping in dB is:
L = 20 × log (voltage ratio V2 / V1) in dB.        V1 = Vin is the reference.

In physics, attenuation is regarded as a positive value.
This naturally leads to sign errors when entering numbers.

 3 dB ≡  1.414 times the voltage    (−)3 dB ≡  damping to the value 0.707
 6 dB ≡          2 times the voltage    (−)6 dB ≡  damping to the value 0.5
10 dB ≡  3.162 times the voltage    (−)10 dB ≡  damping to the value 0.316
12 dB ≡  4 times the voltage    (−)12 dB ≡  damping to the value 0.25
20 dB ≡       10 times the voltage     (−)20 dB ≡  damping to the value 0.1

Using voltage we get: Level in dB: L = 20 × log (voltage ratio)

  6 dB = twice the voltage
12 dB = four times the voltage
20 dB = ten times the voltage
40 dB = hundred times the voltage

If we consider audio engineering, we are usually not interested in power.
Do not ask what power amplification means.
Leave that to the telephone companies or the transmitting aerials (antennas).
Power gain is really not used in audio engineering.
Do we really need power (energy) amplification?
Read the text at the bottom.

 3 dB ≡  2 times the power    (−3) dB ≡  damping to the value 0.5
 6 dB ≡          4 times the power    (−6) dB ≡  damping to the value 0.25
10 dB ≡  10 times the power    (−10) dB ≡  damping to the value 0.1
12 dB ≡  16 times the power    (−12) dB ≡  damping to the value 0.0625 
20 dB ≡       100 times the power     (−20) dB ≡  damping to the value 0.01

Using power we get: Level in dB: L = 10 × log (power ratio)

   3 dB = twice the power
   6 dB = four times the power
 10 dB = ten times the power
 20 dB = hundred times the power 

If you search for the amplification ratio, given the dB value,
then go to the program dB calculation

Amplification (Gain) and Damping (Loss)

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Gain ratio v = V2/V1
for field quantities, e.g. voltage
 		  ↔  Amplification level L (gain)  
voltage level
dB
Formula Factor   Formula Amplification
Voltage gain v = 1 ≡ 0 dB

In audio technique the following "power or energy amplification " is rather unusual.

Gain ratio v = P2/P1 
for energy quantities, e.g. power
 		  ↔  Amplification level L (gain)  
power level
dB
Formula1   Formula2
Power gain v = 1 ≡ 0 dB
  Voltage/Pressure 
  amplification ratio  		   1  
 		  1.414 
= √2		   2  
 		  3.16
= √10		   4  
 		  10 
 		  20 
 		  40 
 		  100 
 		  1000 
 
  Increasing of x dB  0   3   6   10   12   20   26   32   40   60 

  Power/Intensity  
  amplification ratio  		   1  
 		  1.414 
= √2		   2  
 		  3.16
= √10		   4  
 		  10 
 		  20 
 		  40 
 		  100 
 		  1000 
 
  Increasing of y dB  0   1.5   3   5   6   10   13   16   20   30 

Aha!
 
At the cut-off frequency fc the dropped voltage is always fallen to the value of
1/√2 = 0.7071 (70.7%) and the voltage level L is damped to 20 × log10 (1/√2) = (−)3.0103 dB. 
 
At the cut-off frequency fc the dropped power is always fallen to the value of
1/2 = 0.5 (50%) and the power level L is damped to 10 × log10 (½) = (−)3.0103 dB.
 

Aha!
 
The expressed voltage gain in dB (voltage amplification) at the cutoff frequency fc is
20 × log10 (1/√2) = (−)3.0103 dB less than the maximum voltage gain.
 
The expressed power gain in dB (power amplification) at the cutoff frequency fc is
10 × log10 (½) = (−)3.0103 dB less than the maximum power gain.
 

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Voltage V  
volts		  ↔  Voltage level LU 
dBV
Formula Volt   Formula Level
Reference voltage V0 = 1 Volt ≡ 0 dBV
Voltage V (Audio) 
volts		  ↔  Voltage level LU (Audio)
dBu
Formula Volt   Formula Level
Reference voltage V0 = 0.7746 Volt ≡ 0 dBu

The voltage is always given as RMS value - but that is not valid for electric power.

Electric power P  
watts		  ↔  Electric power level LP 
dB
Formula1   Formula2
Reference electric power P0 = 1 W ≡ 0 dB

There is also the reference power P0 = 1 milliwatt or 0.001 watt ≡ 0 dBm

Electric power P (Telephone)  
watts		  ↔  Electric power level LP
dBm
Formel   Formel
Reference electric power P0 = 1 milliwatt = 0.001 watt ≡ 0 dBm

Level in psycho acoustics as subjectivly perceived loudness (volume)
The vague human feeling of the double loudness (volume) is specified
with about 6 to 10 dB. This personal feeling is not an exactly measurable value.
Conversion Factor, Ratio, or Gain to a Level Value (Decibels dB)
Amplifier conversion – Convert decibels to voltage gain / loss
Calculator Voltage Gain – Voltage Loss and Power Gain – Power Loss

Conversion: Gain G, Voltage ratio AV, and Power ratio AP
 
Gain G  dB    |    Voltage ratio (factor) AV    |    Power ratio (factor) AP 
    |     |  
      ↓   |         ↓   |       ↓
    |     |  
 Voltage ratio (factor) AV    |   Voltage gain GV  dB    |  Power gain GP  dB 
Power ratio (factor) AP    |      |  
 
 
Voltage gain Amplification Factor Power and Decibels in dB
 
 
Power gain Amplification Factor Power and Decibels in dB
 
Voltage ratio 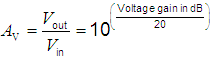Amplification Factor Power and Decibels = amplification factor (voltage)
Power ratio 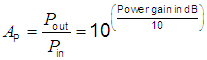Amplification Factor Power and Decibels = amplification factor (power)
gain and loss
V1 = Vin and V2 = Vout.
V2 > V1 or Vout > Vin means amplification. The dB value is positive. (+)
V2 < V1 or Vout < Vin means damping. The dB value is negative. (−)
V2 / V1 or Vout / Vin means the ratio. The amplification or the damping in dB is:
L = 20 × log (voltage ratio V2 / V1) in dB.        V1 = Vin is the reference.
 
Aha!
 
The word "power amplifier" is a misnomer - especially in audio engineering.
Voltage and current can be amplified. The strange term "power amplifier" has
become understood to mean an amplifier that is intended to drive a load such
as a loudspeaker.
We call the product of current gain and voltage gain "power amplification".
 
 
 
 
back zurück Search Engine weiter home start