

| Deutsche Version |
Fill in the gray top box and click on the calculation button. 1 Pa = 1 pascal = 1 N/m2.
| The atmospheric pressure is not the same as the sound pressure. Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average, or equilibrium) atmospheric pressure caused by a sound wave. The sound pressure p are the pressure fluctuations in air that the static air pressure is superimposed. The standard atmospheric pressure is 101,325 pascals = 1,013.25 hPa = 101.325 kPa ● 1,000,000 µPa = 1 Pa = 1 N/m2 ≡ 94 dBSPL (and 1 bar = 105 Pa) 20,000,000 µPa = 20 Pa = 20 N/m2 ≡ 120 dBSPL 1 µPa = 10−6 Pa = 10−6 N/m2 ≡ −26 dBSPL 1 kPa = 103 Pa = 1,000 Pa = 1,000 N/m2 ≡ 154 dBSPL SPL = Sound Pressure Level (SIL = Sound Intensity Level) |
| Sound pressure p (RMS) as Sound field quantity: The auditory threshold is used as the reference sound pressure p0 = 20 µPa = 2 × 10−5 Pa. The threshold of hearing corresponds to the sound pressure level Lp = 0 dB at f = 1 kHz. Sound intensity I as Sound energy quantity: The auditory threshold is calculated as the reference sound intensity I0 = 10−12 W/m2. The threshold of hearing corresponds also to the sound intensity level LW = 0 dB at f = 1 kHz. Sound pressure p = √ (I × Z0) Sound intensity I = p2 / Z0 acoustic impedance Z0 = 400 N·s/m3 |
What does sound level mean?
| A reduction of the sound power level of the sound source by 6 dB is resulting in a reduction of the sound pressure level and the sound intensity level at the location of the receiver by also 6 dB, even if the sound power drops to a factor of 0.25, the sound pressure dropsto a factor of 0.5 and the sound intensity drops to a factor of 0.25. The reference value for the sound level was chosen so that with a characteristic acoustic impedance of Z0 = ρ · c = 400 N·s/m3 the sound intensity level results in the same value as the sound pressure level. We therefore simply speak of the "sound level" and leave it open whether sound pressure level or sound intensity level is meant.
|
| Sound pressure and Sound pressure level 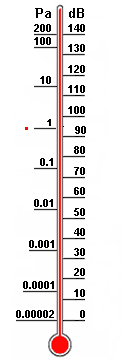 |
|
| The sound pressure or acoustic pressure (alternating pressure changes) is a dynamic pressure. However, the air pressure (atmospheric equal pressure) is a static pressure. The dynamic sound pressure is superimposed on the static air pressure (atmospheric pressure). |
Sound pressure, Sound intensity and their Levels
| The following calculator shows the often desired direct conversion of sound pressure to sound intensity and vice versa with the specific acoustic impedance of air Z0 = 400 N·s/m3. Sound level is given in dB (decibel). |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| While the sound pressure level in the air is matched with the sound intensity level when a reference sound characteristic impedance Z0 = 400 N·s/m³ is chosen, this is not the case with the distance independent sound power level. |
| Sound pressure and Sound power − Effect and Cause |
| Note! Since the sound power level is difficult to measure, it is common to use sound pressure level (SPL) measured in decibels instead. Doubling the sound pressure raises the sound pressure level by 6 dB. |
| Subjectively perceived loudness (volume), objectively measured sound pressure (voltage), and theoretically calculated sound intensity (acoustic power) |
| Psychoacoustic: Relationship between phon and sone |
Sound level change and the ratio (gain)
Be precise: Double the sound pressure and double the sound power, or double the acoustic intensity
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
Sound pressure level SPL and sound pressure
| "Sound level" is the sound pressure level in dB SPL or the sound intensity level in dB SIL. For Pa say, Pascal. This is the size for the pressure p = force F by area A. The reference sound pressure is p0 = 20 µPa = 2×10−5 Pa. The reference sound intensity is I0 = I0 = 10−12 W/m2. DAGA and also DIN request the indication of the sound level in dB alone. The attached SPL comes from the United States and is frowned by acousticians. The often used term "intensity of sound pressure" is not correct. Use "magnitude", "strength", "power", "effectiveness", "amplitude" or "level" instead. "Sound intensity" is sound power per unit area, while "pressure" is a measure of force per unit area. Intensity as sound energy quantity is not the same as pressure as field quantity. |
Sound pressure is not intensity
| Differentiate: Sound pressure p is a "sound field quantity" and sound intensity I is a "sound energy quantity". In teachings these terms are not often separated sharply enough and sometimes are even set equal. |
| Notice, that the calculation I ~ p2 is effective for progressive plane waves. It can be seen that "sound intensity" (acoustic intensity) may never be equated with "sound pressure". The sound pressure is the alternating sound pressure as RMS value. The sound pressure amplitude is the peak value of the sound pressure. The sound volume (loudness) is determined mostly by the sound pressure p and expressed as sound pressure level Lp in dB. |
Comparison of sound pressure level SPL and sound intensity level
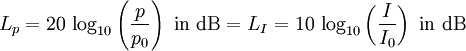 |
| Note: Membranes (diaphragms) of microphones and our eardrums are moved by sound pressure deviations, that is a sound field quantity. However, the sound intensity is a sound energy quantity. |
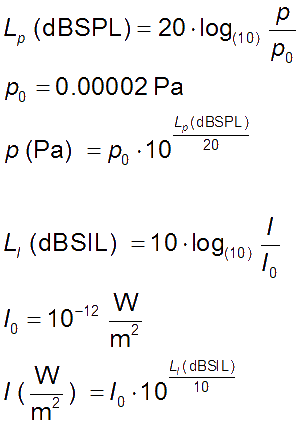
Reference values (hearing threshold): p0 = 20 µPa = 2 × 10−5 Pa or also I0 = 10−12 W/m2.
The sound pressure is always the sound excess pressure as RMS value.
Compare sound power level and sound pressure level in a distance
Table of Sound Pressure and Sound Intensity Levels
![]()
Sound pressure, Sound intensity and their Levels
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
Sound under water, scroll to bottom.
| To speak of the intensity of the sound pressure is nonsense. Sound pressure and sound intensity are really not the same. Do not abuse the word "intensity", unless you really mean the "sound power per area" as W/m². Use "magnitude", "strength", or "level" instead. "Sound intensity" is sound power (acoustic power) per unit area, while "pressure" is a measure of force per unit area. Intensity is not equivalent to pressure. "Amplitude" belongs more to the sound field quantities. |
| Sound intensity = sound pressure × particle velocity Sound intensity = (force / area) × (particle displacement / time) Sound intensity = sound energy / (area × time) = sound power / area. I = p × v = (F / A) × (ξ / t) = E / (A × t) = Pac / A. |
| Note - Comparing dB and dBA: There is no conversion formula for measured dBA values to sound pressure level dBSPL or vice versa. |
| The auditory threshold at 0 dBSPL without weighting cannot be the same as 0 dBA with dBA-weighting for broadband noise. Only for a pure tone of 1 kHz both values can be set equal. There is no "dBA" entry for the threshold of human hearing. For white noise in the audio band from 20 Hz to 20 kHz, the difference between dB and dBA is about 2 dB. |
|
|
|
| The sound pressure p decreases with 1/r from the sound source. The behavior is not inverse-square, but r is inverse-proportional: p ~ 1 / r. |
|
| Intensity = power / area I = P/A = P/(4πr2) Level damping is 6 dB per distance doubling r |
See also: Weighting filter- calculation frequency f to dBA
What is the threshold of pain?
You can find the following rounded values in various audio articles:
| Sound pressure level Lp |
Sound pressure p |
| 140 dBSPL | 200 Pa |
| 137.5 dBSPL | 150 Pa |
| 134 dBSPL | 100 Pa |
| 120 dBSPL | 20 Pa |
| The threshold of pain is known in acoustics as the lowest strength of a stimulus, that is perceived by the ear as painful. Because of the different sensitivity of people it cannot be given an accurate value. |
| Permissible Exposure Time Guidelines – Sound Pressure Level - SPL (Dose) How long can a person endure a certain noise level before hearing impairment occurs? |
| Sound Pressure Level | Sound pressure | Permissible Exposure Time |
| 115 dB | 11.2 Pa | 0.46875 minutes (~30 sec) |
| 112 dB | 7.96 Pa | 0.9375 minutes (~1 min) |
| 109 dB | 5.64 Pa | 1.875 minutes (< 2 min) |
| 106 dB | 3.99 Pa | 3.75 minutes (< 4 min) |
| 103 dB | 2.83 Pa | 7.5 minutes |
| 100 dB | 2.00 Pa | 15 minutes |
| 97 dB | 1.42 Pa | 30 minutes |
| 94 dB − − − − − − − − − − | 1.00 Pa − − − − − − | 1 hour − − − − − − − − − − − − − − |
| 91 dB | 0.71 Pa | 2 hours |
| 88 dB | 0.50 Pa | 4 hours |
| 85 dB | 0.36 Pa | 8 hours |
| 82 dB | 0.25 Pa | 16 hours |
| Accepted guidelines for recommended permissible exposure time for continuous time weighted average noise, according to NIOSH-AINSI and CDC. For every 3 dB sound pressure level (SPL) over 85 dB, the permissible exposure time is cut in half − before damage to our hearing can occur. NIOSH = National Institute for Occupational Safety and Health and CDC = Centers for Disease Control and Prevention. OSHA = Occupational Safety and Health Administration. NIOSH represents the use of an 8-hour exposure of noise at 85 dBA and a 3 dBA doubling rate, to determine the noise dose. OSHA represents the use of an 8-hour exposure of noise at 90 dBA and a 5 dBA doubling rate, which does not protect many workers from hearing loss over their whole working lifetime. This may not represent a worldwide view of the subject. Noise is an increasing public health problem and can have the following adverse health effects: hearing loss, sleep disturbances, cardiovascular and psychophysiological problems, performance reduction, annoyance responses, and adverse social behaviour. A person feels and judges sound events by exposure time, spectral composition, temporal structure, sound level, information content and subjective mental attitude. |
To determine SPL and exposure time
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| Conversion: sound pressure, particle velocity, acoustic impedance, and intensity Table of sound levels (pressure and also intensity) |
| Sound Field quantities Sound pressure, sound or particle velocity, particle displacement or displacement amplitude, (voltage, current, electric resistance). Inverse Distance Law 1/r |
Sound Energy quantities Sound intensity, sound energy density, sound energy, acoustic power. (electrical power). Inverse Square Law 1/r² |
| Sound (or acoustic) pressure is the fluctuation in pressure caused by a sound (acoustic) wave. Sound power (or acoustic energy) is the amount of energy contained in a sound (acoustic) wave. It's unfortunate that the terms 'power' and 'energy' get so badly intermixed in acoustics. They really aren't the same thing at all. Energy is the capacity to 'do' something. Power is the amount of energy used (or generated) per unit of time. |
| Hearing is directly sensitive to sound pressure. Only the sound pressure moves our eardrums. In stereo history the level differences have been called "intensity" differences, but sound intensity is a specifically defined size and cannot be sensed by a simple microphone, nor would it be of value in music recordings if it could be. "Intensity" stereophony is better termed as level difference stereophony. |
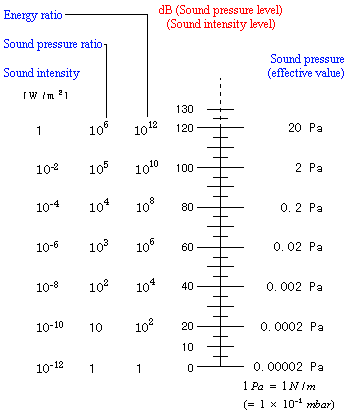 |
Important to notice: 1 Pa = 1 N/m2 ≡ 94 dB and 1 bar = 105 Pa.
| ASACOS Rules for Preparation of American National Standards in ACOUSTICS, MECHANICAL VIBRATION AND SHOCK, BIOACOUSTICS, and NOISE states:
3.16 Unit symbols - 3.16.1 When to use unit symbols in the text of the standard, the unit symbol for a size shall be used only when the unit is preceded by
a numeral. When the unit is not preceded by a numeral, spell out the name of the unit. In text, even when a numerical value is given, it is desirable to spell out
the name of the unit. Moreover, the name shall be spelled out when it first appears in the text, and more often if the text is lengthy. Thus, in text write "...a
sound pressure level of 73 dB; or "...a sound pressure level of 73 decibels." Do not write "sound pressure level in dB"; the correct form is "sound pressure level
in decibels." Do not write "dB levels", "dB readings", or "dB SPL". Levels or readings are not of decibels; they are of sound pressure levels or some other
acoustical size. Write out the word "decibel" for such applications, and be sure that the word 'decibel' follows, not precedes the description of the relevant
acoustical size. The guidelines given for the National Standards clearly excludes the use of "dB SPL". The reference added to the decibel article ends up being a document that merely includes "dB SPL" in a list of terms. The glossary within the same document does not even list this supposed term, even though weighted decibel terms are defined. The glossary in the file does have an entry for "sound pressure level': (1) Ten times the logarithm to the base ten of the ratio of the time-mean-square pressure of a sound, in a stated frequency band, to the square of the reference sound pressure in gases of 20 micropascals (µPa). Unit, dB; symbol, Lp. (2) For sound in media other than gases, unless otherwise specified, reference sound pressure in 1 µPa (ANSI S1.1-1994: sound pressure level). A reference level of 20 µPa is often used. In general, it is necessary to know the reference level when comparing measurements of SPL. The unit dB (SPL) is often abbreviated to just "dB", which gives some the erroneous notion that a dB is an absolute unit by itself. |
| How does sound level depend on distance from the source? Damping of sound level with distance from sound source http://www.sengpielaudio.com/calculator-distance.htm |
|
Intensity I is defined as the power per unit area. The surface area of the sphere is A = 4 π r2, so the sound power P passing through each square metre of surface is the intensity: I = P / A = P / 4 π r2. We see that, for a uniformly radiating sound source, sound intensity is inversely proportional to the square of the distance r away from the source: I2 / r12 = I1 / r22. But sound intensity is proportional to the square of the sound pressure, so we could equally write: p2 / p1 = r1 / r2. We see that sound pressure falls inversely proportional to the distance r away from the source. If we double the distance, we reduce the sound pressure by a ratio of 2 and the sound intensity by a ratio of 4. In other words, we reduce the sound level by (−)6 dB. |
| Often it is confusing that the sound pressure p as a sound field quantity decreases with 1 / r of the distance but the sound intensity I as a sound energy size decreases with 1/r2. I is proportional to p2. Sound field parameters: Sound pressure, sound (particle) velocity, particle displacement. These terms are all proportional to the electric voltage, electric current, and the electrical resistance. Sound energy parameters: Sound intensity, sound energy, sound energy density, sound performance. To all this, the power is proportional. Intensity is called colloquially the way in which something is operated: intense, driven, focused. Intensity is, however, especially in physics and acoustics, and it is important technical term for the energy alone. The word intensity is quite often incorrectly used for strength, force, amplitude and level. Therefore, the term intensity should be taken only if really the (radiation) energy is meant. In sound recording technology with microphones it is almost always the strength, the amplitude or the level that is meant and only as a rare exception the sound intensity (energy) is wanted. Even the "intensity" stereophonc system does not work with sound intensities but is working with linear sound pressure differences. What moves the microphone's diaphragms and also our eardrums? It is simply the sound pressure and not the sound intensity. The sound pressure is the function of the time and place of the sound pressure fluctuations Δ p as an overlay to the atmospheric pressure. The sound pressure effect is moving our eardrums and is therefore relevant to the perception of sound. |
Sound Level Comparison Chart
| Table of sound level dependence and the change of the respective ratio to subjective loudness (volume), objective sound pressure (voltage), and sound intensity (acoustic power). How many decibels (dB) level is double, half, or four times as loud? How many dB to appear twice as loud? Here are all the different ratios. |
| Level Change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31.6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - - - | - - - - - 1.0 - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 0.25 | 0.100 | 0.01 |
| −30 dB | 0.125 | 0.0316 | 0.001 |
| −40 dB | 0.0625 | 0.0100 | 0.0001 |
| Log. size | Psycho quantity | Field quantity | Energy quantity |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
| For a 10 dB increase of the sound level we require ten times more power from the amplifier. This increase of the sound level means for the sound pressure a lifting of the ratio 3.16. Loudness and volume are highly subjective. That belongs to the domain of psychoacoustics. |
|
Sound level, loudness, and sound pressure are not the same things. There are fluctuations in individual perception of the strength of sound. The sound pressure measured twice as much gives 6 dB more level. The sound perceived twice as loud needs roughly a sound level increase by 10 dB. The human perception of loudness is perceived differently from each subject. In other words it is one's own perception of sound and it is subjective of sound pressure level SPL. |
| Notice – The sound pressure as sound field quantity is not the same as the sound intensity as sound energy size. |
Sound pressure and sound power
Correlation of volume and loudness − sone and phon
conversions and Calculations - Sound sizes and their Levels
Frequently used false statements in the context of
sound values and the distance of the sound source
The sound pressure decreases from a point source with 1/r after the distance law.
| Correct version | Wrong expression |
| Sound pressure (amplitude) falls inversely proportional to the distance 1/r from the sound source. That is the 1/r law or the inverse distance law. |
Sound pressure (amplitude) falls inversely proportional to the square of the distance 1/r2 from the sound source. really wrong |
| Sound pressure level decreases by (−)6 dB for doubling of the distance from the source to 1/2 (50 %) of the sound pressure initial value. |
Sound pressure level decreases as the distance increases for doubling of the distance from the source by (−)3 dB. wrong |
| Sound intensity (energy) falls inversely proportional to the square of the distance 1/r2 from the sound source. That is the inverse square law 1/r2. |
Sound intensity (energy) falls inversely proportional to the distance 1/r from the sound source. wrong |
| Sound intensity level decreases by (−)6 dB for doubling of the distance from the source to 1/4 (25 %) of the sound intensity initial value. |
Sound intensity level decreases inversely as the square of the distance increases for doubling of the sound source by (−)3 dB. wrong |
Sound pressure is not intensity
| Neither the sound power nor the sound power level decreases in doubling the distance. Why is this so? The sound power level quantifies the totally radiated sound energy from an object. Different to the sound pressure the sound power is independent of the distance to the sound source, the surrounding area and other influences. |
|
Differentiate: Sound pressure p is a "sound field quantity" and sound intensity I is a "sound energy quantity". In teachings these terms are not often separated sharply enough and sometimes are even set equal. But I ~ p2. |
|
Question: How does the sound power decrease with distance"? Answer: "April fool - The sound power does not decrease (drop) with distance from the sound source." Levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source. Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. A frequent question: "Does the sound power depend on distance?" The clear answer is: "No, not really." We consider sound fields in air which are described by the scalar quantity p (sound pressure) and the vector quantity v (sound velocity) as a sound field quantity. |
Sound pressure and sound level under water
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| Conversion of dB between air to water |
| In 1970, the pressure reference level of 0 dB ≡ 1 µPa was chosen by the US Navy for their underwater work for sound in water. Furthermore, airborne sound pressure levels are often referred to as frequency-weighted sound pressure level indicated by the frequency response of human hearing. For the evaluation of the influence of underwater sound on marine animals there is no useful reference scale. The difficult comparison of noise data in air and in water provides sound in discussions about the harm of sonars and echo sounders and sounds of marine animals always show confusion. The most important measure of the sound of water is used as the sound produced by the sound pressure level (SPL). Although formally the same methods can be employed for water noise and air noise it is difficult to be compared and lead to serious misunderstandings. Levels are logarithmic values and interpret meaningful values only if the reference values used in each case be respected. The reference value for the sound pressure level in air is selected at 20 µPa, the reference sound of water on the other hand is 1 µPa. The reference value for airborne sound has been selected on the basis of the human hearing threshold and corresponds to a plane wave propagation in the medium of air to a sound pressure of about 2×10−5 pascals (20 µPa). The reference sound pressure corresponds to a sound intensity of about 10−12 W/m². Water is much harder than air, so much for the same intensity of the acoustic particle velocity is less relevant, but the sound pressure is greater. For this reason, a comparison of the sound pressure is not useful anyway. If you want to compare the energy flux density (intensity) should be used. Because the measured sound pressure is technically more accessible, we take it anyway. The intensity of the underwater sound in which used therein reference pressure of 1 µPa corresponds to an intensity of about 0.65×10−18 W/m². The relationship between sound pressure and sound intensity are also a part of air pressure, depending on its temperature and salinity of the water. Approximately the same level of detail for air and water at their respective reference pressure in level differ by approximately 62 dB. For a comparability of the levels - anyway in question - withdraw from the pressure level under water about 62 dB. The large difference between the level of sound in air and the indication of the sound level under water specified in decibels (dB) is seldom recognized and clearly explained. |
How is sound in water different from sound in air?
How does sound in air differ from sound in water?
| Comparing sound levels in air against sound levels in water must be done very carefully. First, by accepted convention, the reference pressure values are different by 26 dB. Second, due to the difference in impedance (the stiffness or density of the medium) between air and water, roughly a 3,500 times greater power level (36 dB) is required in air to produce an equivalent pressure level in water. Combining these two values, a 26 dB + 36 dB = 62 dB difference, or correction factor, between the two scales is required. Therefore, 62 dB must be subtracted from a sound level in water to produce an equivalent acoustic intensity in air. It is misleading to compare the decibels of the underwater sound with the decibels of sounds heard in the air. |
| Microphones that are used under water are called hydrophones. It is possible to get these special microphones at the firm DPA. Usual Microphones must be protected from water. Imaginative engineers on location draw a condom on conventional microphones, when recording in the situation of rain or under water in a swimming pool. This is no joke. The slack latex skin seals the microphone capsule from water and the sound pressure fluctuations (scalar) are transmitted - but this trick is applicable only for pure pressure receivers, that means when microphones are omnidirectional. That does not work with pressure gradient microphones like cardioids, because the motion of the pressure gradient, that is the pressure difference before and behind the diaphragm as a vector, is horribly disturbed by the condom. In the "YouTube" tips making microphones watertight or waterproof, they forget to explain that this really does not work correctly for cardioid microphones, and other pressure gradient microphones. They don't know it better; see: YouTube: Waterproofing a microphone with a condom The advice to use a soundfield microphone for a surround sound recording under water with a condom, had to be recognized as nonsense, since the four necessary pressure gradient microphones lose completely the effect. |
| Note: Only microphones with omnidirectional polar patterns work correct with condoms under water. |
| Calculations and conversions of pressure units More conversions of pressure and stress units conversions of pressure units |
| Question: What is the standard distance to measure sound pressure level away from equipment? There is no standard distance. It depends on the size of the sound source and the sound pressure level. |
Weighted Sound is not given in phon, but in dB(A).
| Relationship between Sound Pressure and Sound Power Sound Power and Pressure Measurements How does the sound decrease with distance? |
| Conversion of sound units Sound intensity: Reference sound intensity I0 = 10−12 W/m2 (hearing threshold) Reference sound intensity level LI0 = 0 dB-SIL (hearing threshold) Get sound intensity I when entering sound intensity level LI: I = I0×10(LI/10) in W/m2 = 10−12×10(LI/10) in W/m². Get sound intensity level LI in dB when entering sound intensity I in W/m2. LI = 10×log (I / I0) in dB = 10×log (I / 10−12) in dB. Sound pressure: Reference sound pressure p0 = 20 µPa = 2×10−5 Pa (hearing threshold) Reference sound pressure level Lp0 = 0 dB-SPL (hearing thresholdl) Get sound pressure p when entering sound pressure level Lp: p = p0×10(Lp/20) in Pa (= N/m2) = 2×10−5×10(Lp/20) in Pa (N/m2). Get sound pressure level Lp in dB when entering sound pressure p in Pa: Lp = 20×log (p / p0) in dB = 20×log (p / 2×10−5) in dB. How to add two sound intensity levels LI1 = 50 dB and LI2 = 65 dB? Get out of dB and back to ratio. (Energy size.) (The reference sound intensity is not used here.) I1 = 10(LI1/10) = 10(50/10) = 100000. I2 = 10(LI2/10) = 10(65/10) = 3162277. Add them to get I = I1 + I2 = 3262277. Now get back to dB: LI = 10×log (3262277) = 65.13 dB. For large dB differences over 10, just take the highest value. How do you add two sound pressure levels Lp1 = 50 dB and Lp2 = 65 dB? Get out of dB and back to ratio. (Field quantity.) (The reference sound pressure is not used here.) p1 = 10(Lp1/20) = 10(50/20) = 316. p2 = 10(Lp2/20) = 10(65/20) = 1778. Pythagoras: p = √ (p12+p22) = √ (3162 + 17782) = 1806. Now get back to dB: Lp = 20×log (1806) = 65.13 dB. For large dB differences over 10, just take the highest value. |
| What is the highest sound pressure possible? How many decibels is the loudest noise? |
| A typical false statement: "No noise levels can exceed 194 dB ever." Is the end at 194 dB? In addition to this perception threshold is discussed more often a physical limit to 194 dB. Sound is nothing more than a minor disturbance of air pressure and 194 dB is theoretically the same as the disturbance itself. It must be distorted. Even louder noise is possible, but heavily distorted. That's chaos. This high sound pressure will break all measurement microphones and human beings are completely torn when they are close to the center of a nuclear explosion. No hearing protection (ear muffs or ear plugs) can help you there. |
| Some information about Hearing Level (HL) Pure-tone audiometric thresholds are expressed in dB HL. |
| Frequency | dB SPL | dB HL |
| 250 Hz | +15.0 | 0.0 |
| 500 Hz | +9.0 | 0.0 |
| 1000 Hz | +3.0 | 0.0 |
| 2000 Hz | −3.0 | 0.0 |
| 4000 Hz | −4.0 | 0.0 |
| 8000 Hz | +13.0 | 0.0 |
| back |
Search Engine |
home |