

| Deutsche Version |
| ● Levels and References of the Sound Quantities ● Calculations and Formulas around the Decibel (dB) |
|
Sound pressure p (RMS) as Sound field quantity: The auditory threshold is used as the reference sound pressure p0 = 20 µPa = 2 × 10−5 Pa. The threshold of hearing corresponds to the sound pressure level Lp = 0 dB at f = 1 kHz. Sound intensity I as Sound energy quantity: The auditory threshold is calculated as the reference sound intensity I0 = 10−12 W/m2. The threshold of hearing corresponds also to the sound intensity level LW = 0 dB at f = 1 kHz. The loudness of the sound, however, is a psychoacoustic measure of how loud a sound from certain people as acoustic event is sensed. The loudness (volume) represents the physically measurable amplitude or strength of the sound, for example, as compared with sound pressure or sound pressure level than that perceived by humans as loudness. The perceived loudness is a psycho-acoustic quantity that depends on several factors: the sound pressure level, the frequency spectrum, and the time behavior of the sound. Volume can not be easily measured. Readings of a pure 1 kHz tone should be identical, whether weighted or not. |
Sound pressure, Sound intensity and their Levels
| The following calculator shows the often desired direct conversion of sound pressure to sound intensityand vice versa with the specific acoustic impedance of air Z0 = 400 N·s/m3. |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| While the sound pressure level in the air is matched with the sound intensity level when a reference sound characteristic impedance Z0 = 400 N·s/m3 is chosen, this is not the case with the distance independent sound power level. |
What does sound level mean?
A reduction of the sound power level of the sound source by 6 dB is resulting in a reduction of the sound
pressure level and the sound intensity level at the location of the receiver by also 6 dB, even if the sound
power drops to a factor of 0.25, the sound pressure drops to a factor of 0.5 and the sound intensity drops
to a factor of 0.25. The reference value for the sound level was chosen so that with a characteristic acoustic
impedance of Z0 = ρ · c = 400 N·s/m3 the sound intensity level results in the same value as the sound
pressure level. We therefore simply speak of the "sound level" and leave it open whether sound pressure
level or sound intensity level is meant.
|
There is also the reference power P0 = 1 milliwatt = 0.001 watt ≡ 0 dBm.
Sound quantities: Differentiate between sound field quantities and sound energy quantities
| Sound field quantites (sizes)
Sound pressure, sound or particle velocity, particle displacement or particle amplitude, (voltage, current, electric resistance). Inverse Distance Law 1/r |
Sound energy quantities (sizes) Sound intensity, sound energy density, sound energy, acoustic power. (electrical power). Inverse Square Law 1/r² |
|
Since sound measuring instruments (meters) respond to sound pressure the "decibel"
is generally associated with sound pressure level. Sound pressure levels quantify in
decibels the strength (not intensity!) of given sound sources. Sound pressure levels
vary substantially with distance from source, and also diminish as a result of intervening
obstacles and barriers, air absorption, wind and other factors. Sound Pressure Level (SPL): 20×log (p/p0) = 10×log (p/p0)2, where p0 = 2×10−5 N/m2. p = root mean square sound pressure (N/m2 = Pa). The usual reference level p0 is 20×10−6 Pa, the auditory threshold. Note that the noise from motors is documented in sound power (acoustic power) level. "Threshold of audibility" or the minimum pressure fluctuation detected by the ear is less than 10−9 of atmospheric pressure or about 2×10−5 Pa (pascal) at 2000 Hz. "Threshold of pain" corresponds to a pressure 106 times greater, but still less than 1/1000 of atmospheric pressure. The standard air pressure is 101325 Pa = 101.325 kPa or 1013.25 hectopascal. Because of the wide range, sound pressure measurements are made on a logarithmic decibel scale. Sound power levels are connected to the sound source and are independent of distance. Sound power levels are indicated in decibels. Lw = 10×log (P / P0) where the reference power P0 = 10−12 W, calculated from p0 = 20 micropascals, which is the lowest sound persons of excellent hearing can discern. Sound power is measured as the total sound power emitted by a source in all directions in watts (joules / second). Sound power levels do not vary with distance from source. |
|
Questions: 1. How many decibels (dB) is the sound pressure p = 1 Pa? 2. How many decibels (dB) is the acoustic intensity I = 1 W/m2? 3. How many decibels (dB) is the acoustic power Pac = 1 W? 4. How many decibels (dB) is the particle velocity v = 1 m/s? 5. How many decibels (dB) is the sound energy density w = 1 J/m3? The calculators above can help with the answers. |
| How many decibels (dB) is the level of the sound energy W = I×t×A in J = W×s? This question is found quite rarely. For calculations we use more the sound energy quantities: sound energy density, w or E = I / c in J/m3, sound intensity I = Pac/A in W/m², and sound power Pac in W = J/s, and their corresponding levels. |
|
Note: The radiated sound power (sound intensity) is the cause and the sound pressure is the effect, where the sound engineer is particularly interested in the effect. The effect of temperature and sound pressure: Sound pressure and Sound power – Effect and Cause. |
| Acousticians and sound protectors ("noise fighters") need the sound intensity (acoustic intensity) – but sound engineers and sound designers ("ear people") don't need that sound energy quantity. Who is involved in audio engineering, should rather take care of the sound field quantity, that is the sound pressure or the sound pressure level (SPL) as an effect at the eardrums of our hearing and on the diaphragms of the microphones, and the corresponding audio voltage and its voltage level. |
Sound pressure and Sound power − Effect and Cause
Conversion of Factor or Ratio to Level Value (Decibels dB)
| Table of Sound Levels, Sound Pressure, and Sound Intensity Conversion of Sound Units (Levels) Damping of Sound Level with Distance |
Frequently used false statements in the context of
sound values and the distance of the sound source
| Correct version | Wrong expression |
| Sound pressure (amplitude) falls inversely proportional to the distance 1/r from the sound source. That is the 1/r law or the inverse distance law. |
Sound pressure (amplitude) falls inversely proportional to the square of the distance 1/r2 from the sound source. really wrong |
| Sound pressure level decreases by (−)6 dB for doubling of the distance from the source to 1/2 (50 %) of the sound pressure initial value. |
Sound pressure level decreases as the distance increases for doubling of the distance from the source by (−)3 dB. wrong |
| Sound intensity (energy) falls inversely proportional to the square of the distance 1/r2 from the sound source. That is the inverse square law 1/r2. |
Sound intensity (energy) falls inversely proportional to the distance 1/r from the sound source. wrong |
| Sound intensity level decreases by (−)6 dB for doubling of the distance from the source to 1/4 (25 %) of the sound intensity initial value. |
Sound intensity level decreases inversely as the square of the distance increases for doubling of the sound source by (−)3 dB. wrong |
Sound pressure is not intensity
| Neither the sound power nor the sound power level decreases in doubling the distance. Why is this so? The sound power level quantifies the totally radiated sound energy from an object. Different to the sound pressure the sound power is independent of the distance to the sound source, the surrounding area and other influences. |
| Notice: The psychoacoustic subjective sensations of loudness do not belong to those predictable and measurable sound quantities; see: Correlation between volume level in phone and loudness in sone We feel and judge sound events as: − exposure duration − spectral composition − temporal structure − sound level − information content − subjective mental attitude |
| "Sound level" is the sound pressure level in decibel (SPL), or sometimes the sound intensity level in dB (SIL). The reference sound pressure is p0 = 20 µPa = 2 × 10−5 Pa − the reference sound intensity is I = 10−12 W/m2. |
| Differentiate: Sound pressure p is a "sound field quantity" and sound intensity I is a "sound energyquantity". In teachings these terms are not often separated sharply enough and sometimes are even set equal. But I ~ p2. |
| Notice, that the calculation I ~ p2 is effective for progressive plane waves. It can be seen that "sound intensity" (acoustic intensity) may never be equated with "sound pressure". The sound pressure is the alternating sound pressure as RMS value. The sound pressure amplitude is the peak value of the sound pressure. The sound volume is determined by the sound pressure p and expressed as sound pressure level Lp in dB. |
Comparison of sound pressure level SPL and sound intensity level
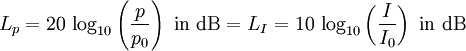 |
| Note: The sound intensity is a sound energy quantity. Membranes (diaphragms) of microphones and our eardrums are moved by sound pressure deviations, that is a sound field quantity. |
Sound Level Comparison Chart and the Ratios
| Table of sound level dependence and the change of the respective ratio to subjective
volume (loudness), objective sound pressure (voltage), and sound intensity (acoustic power). How many decibels (dB) level change is double, half, or four times as loud? How many dB to appear twice as loud (two times)? Here are all the different ratios. Ratio means "how many times" or "how much" ... Doubling of loudness. |
| Level Change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31.6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 0.25 | 0.100 | 0.01 |
| −30 dB | 0.125 | 0.0316 | 0.001 |
| −40 dB | 0.0625 | 0.0100 | 0.0001 |
| Log. size | Psycho size | Field size | Energy size |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
| For a 10 dB increase of the sound level we require ten times more power from the amplifier. This increase of the sound level means for the sound pressure a lifting of the ratio 3.16. Loudness and volume are highly subjective. That belongs to the domain of psychoacoustics. |
The standard atmosphere is 101325 Pa = 101.325 kPa or 1013.25 hectopascal.
| Comparative representation of sound field
quantities and sound energy quantities Relationship of acoustic sizes of a plane progressive acoustic sound wave |
Audio voltage and level
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
Unclear equations in books
| The sound intensity I in W/m2 in a plane progressive wave
is given as: But only one equation can be correct. Sometimes, these equations will show further information: 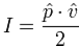 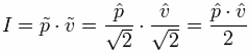 The tilde will indicate that it is the RMS value and the roof will show that it is the amplitude value, ie, the peak value. For sinusoidal signals, the peak value means the amplitude. With these more accurate data, both equations are correct. You just need to know exactly whether the peak value or the RMS value is applied. Sound pressure p in Pa = N/m2 − particle velocity v in m/s − acoustic intensity I in W/m2 that is N/m2 · m/s Energy equivalent: J (joule) = N · m = W · s In audio engineering we always (!) assume RMS values, if not specially noted different. The reference sound pressure is p0 = 20 µPa = 2 × 10−5 Pa and this is the RMS value. |
| What is an Amplitude |
| How does the sound decrease with distance? How does the noise depend on distance from the source? |
| The constant unsureness is the answer of the question: "How many dBs are doubling a sound"? Answer: Doubling means the "factor 2". What does doubling of a"sound" mean? Twice the (sound) intensity is obtained by an increase of the (sound intensity) level of 3 dB. Twice the sound pressure is obtained by an increase of the (sound pressure) level of 6 dB. Twice the loudness feeling is obtained by an increase of the (loudness) level of about 10 dB. |
| The question: "Is noise level really the sound intensity level?" will be differently
answered by musicians and sound engineers as "ear people" than by
acousticians. We measure the sound of music with a sound level meter (SPL meter) and our eardrums are effectively moved by the sound pressure or its level. A sound engineer thinks that a sound level has mainly to do with the sound pressure deviations. Acousticians as "sound fighters" have a slightly different point of view. They mainly like to calculate the energy (power) of the sound. |
 |
| By the way, sellers always want us to buy a sound pressure level meter with digital display. But much better, however, is an analogue-to-read display - as in this figure. If you don't understand: Do you have a wrist watch with good to read analog hands or do you have a digital display there? Why? |
| back |
Search Engine |
home |