Calculation: voltage, power, gain, loss - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
Calculation:
● Voltage Gain and Power Gain ●
• Voltage Loss and Power Loss •

A provocative question: Can one ever amplify the power? Electrical voltage and electrical current can be amplified. Energy can be converted in various forms of energy. To save energy one wants to produce more power with less energy.
The term "amplifier" covers up that the energy comes entirely from the mains and largely leaves the devices as a loss. Because of energy conservation you cannot make a large power from a small power. However, one can at least transfer the data from a weak to a strong current.

Find decibel voltage gain and ratio out/in by entering input and output voltage:

       Input Voltage  volts    
    Output Voltage  volts    
               Gain  dB
Ratio out/in   
    
 

Find decibel power gain and ratio out/in by entering before and after power:
 
Notice: Power gain is not used in audio engineering.

   Power Before  watts   
    Power After  watts
           Gain  dB  
 Ratio out/in        
    

Find output voltage by entering input voltage and voltage gain/loss (dB):

            Input voltage volts 
Voltage gain/loss dB
Output voltage Volt
    

Find output power by entering input power and power gain/loss (dB):
 
Notice: Power gain is not used in audio engineering.

             Input power watts
 Power gain/loss dB
Output power Watt
     
Voltage Ratio and Voltage Level Formula Voltage Level - sengpielaudio
 
Power Ratio and Power Level Formula Power Level
  Not used in Audio

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Gain factor v = V2/V1 
(field quantities, e.g. voltage)
  ↔  Amplification level L  
(voltage level)
dB
FormelVerstaerkungsfaktor    v = Vout / Vin   Formel Verstärkung
Voltage level 0 dB equals voltage amplification v = 1

In audio engineering "power amplification" is unusual, even
power amplifiers for loudspeakers don't amplify the power.
They amplify the audio voltage moving the speaker coil.

Gain factor v = P2/P1
(energy quantities, e.g. power)
  ↔  Amplification level L  
(power level)
dB
Start   v = Pout / Pin   Start
Power level 0 dB equals power amplification v = 1
 
Power is like all energy quantities primarily a calculated value.
 

Aha!
 
The expressed voltage gain in dB (voltage amplification) at the cutoff frequency is
20 · log10 (1/√2) ≈ (−)3.0103 dB less than the maximum voltage gain.
That equals a factor of 0.7071 or 70.71%.
 
The expressed power gain in dB (power amplification) at the cutoff frequency is
10 · log10 (½) ≈ (−)3.0103 dB less than the maximum power gain.
That equals a factor of 0.5 or 50%.
 

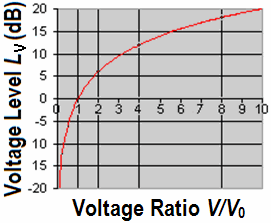
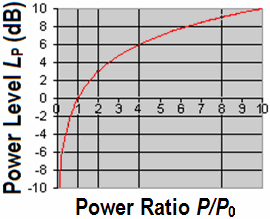
Decibels are defined as ten times the log of a "power ratio". Decibels convert multiplication and division calculations into simple addition and subtraction operations.
But in Audio we never use the power ratio. We like the voltage, sound pressure, or amplitude ratio. For us decibels are defined as twenty times the log of an amplitude ratio.
 
Ratio
(OUT / IN) 		Voltage Gain
(dB)		 "Power Gain"
(dB)
   1/1000    −60    −30
   1/100    −40    −20
   1/10    −20    −10
   1/5    −14    −7
   1/2    −6.02   −3.01
     1      0      0
     2    +6.02    +3.01
     5    +14    +7
   10    +20    +10
   100    +40    +20
   1000    +60    +30
 
Voltage Gain   Power Gain
Voltage ratio
Factor V2/V1		 Voltage amplification
GV in dB		   Power ratio
Factor P2/P1		 Power amplification
GP in dB
103 +60     106 +60  
102 +40     104 +40  
101 +20     102 +20  
√10 = 3.16 +10     10   +10  
2 +6   4 +6
√2 = 1.414 +3   2 +3
1 ±0   1 ±0
1/√2 = 0.7071 −3     1/2 = 0.5 −3
1/2 = 0.5 −6       1/4 = 0.25 −6
1/√10 = 0.316 −10     10−1 = 0.1 −10  
10−1 = 0.1   −20     10−2 = 0.01 −20  
10−2 = 0.01 −40     10−4 = 0.0001 −40  
   10−3 = 0.001 −60     10−6 = 0.000001 −60  
V2/V1 = 10(GV in dB/20) GV = 20×log (V2/V1)   P2/P1 = 10(GP in dB/10) GP = 10×log (P2/P1)
 
Voltage gain (dB) = 20×log (Audio output voltage / Audio input voltage). Used in audio.
Voltage gain is defined as the ratio of the output voltage to the input voltage in dB. Assume that the input voltage is 10 mV (+10 dBm) and the output voltage is 1 V (1000 mV, +60 dBu). The ratio will be 1000/10 = 100, and the voltage gain will be 20×log 100 = 40 dB. Reference voltage V0 = 1 Volt.
 
Power gain (dB) = 10×log (RF output power / RF input power). Used in RF.
Power gain is defined as the ratio of the output power to the input power in dB. Assume that the input power is 10 mW (+10 dBm) and the output power is 1 W (1000 mW, +30 dBm). The ratio will
be 1000/10 = 100, and the power gain will be 10×log 100 = 20 dB. Reference power P0 = 1 Watt.
 
 
 
back back Search Engine forward home start