-3 dB corner frequency cutoff -3dB bandwidth Q factor bandwidth in octaves 3 dB band pass filter bandwidth BW qualiy factor filter vibration center frequency filters conversion converter octave formula -3 dB bandwidth calculator conversion EQ equalizer band-pass filter - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
● Calculation − Equalization − Bandpass − Filter ●
 
Calculating the bandwidth at −3 dB  cut-off frequencies  f1 and f2
when center frequency  f0 and Q factor is given.
The bandwidth BW is between lower and upper cut-off frequency.
 
Filter resonance
 
3 dB bandwidth BW = f2 − f1= f0/Q and quality factor is Q factor
EQ filter conversion Q factor to bandwidth in octaves N
Parametric peak equalizer and notch (dip) equalizer
People use 'Q' and 'bandwidth' interchangeably, though they're not.
Defining the bandwidth for a bandpass as the −3 dB points cannot be correct for a boost gain of 3 dB or less.
 
f1 and f2 = corner frequency = cut-off frequency = crossover frequency
= half-power frequency = 3 dB frequency = break frequency is all the same.
 
The center frequency  f0 is the geometric mean of f1 and f2
BW = Δf = f0 / Q          Q = f0 / BW          f0 = BW × Q = √ (f1 × f2)
BW = f2 − f1            f1 = f02 / f2 = f2 − BW             f2 = f02 / f1 = f1 + BW

 
Center frequency f0   Hz 
Q factor or quality factor Q   
 
          ↓          
 
 Lower cutoff frequency f1   Hz
Upper cutoff frequency f2   Hz
 
Formula for the lower cutoff frequency:
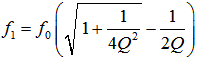Formula f1
Formula for the upper cutoff frequency:
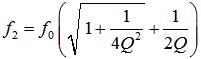Formula f2
 
Formula for the Q factor:
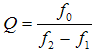Formula f2
Formula for the bandwidth:
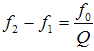Formula f1
 
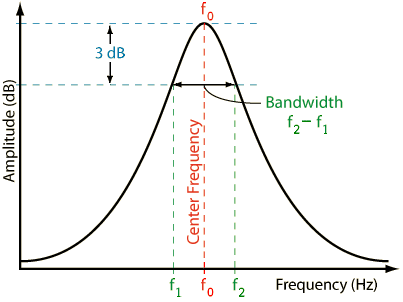
 A high filter quality means narrow-band filtering (notch), with a large Q factor.
 This results in steep filter flanks with a small bandwidth.
 
 A low filter quality means broad-band filtering, with a small Q factor.
 This results in flat filter flanks with a large bandwidth.
 
 
 Notice:
 A low Q factor gives a broad band (wide) bandwidth or  a high Q factor gives a narrow band (small) bandwidth.
 

Q factor as a function of the bandwidth in octaves N (octave bandwidth)

 Bandwidth in 
octaves N		       Q factor      
         3.0 wide          0.404 low
         2.5          0.511
         2.0          0.667
         1.5          0.920
         1.0          1.414
         2/3          2.145
         1/2          2.871
         1/3          4.318
         1/6          8.651
       1/12 small        17.310 high

Conversion: 'bandwidth in octaves' N to quality factor Q
Interrelationship of 'octave bandwidth' N and the quality factor Q
Formulas for conversion of bandwidth in octaves to quality factor
Questions on "Parametric filter adjustment"
Conversion table Q to N and N to Q for parametric filters
Filter slope or steepness (dB/oct) is not bandwidth
Excel conversion - quality factor Q to bandwidth in octaves N
Calculating the center frequency from a given bandwidth
Finding the filter center frequency - geometric mean
Conversion RC-pad − R × C to Corner frequency fc and Cutoff frequency to R × C − Time constant t (tau) = R × C
 
Why is the bandwidth and the cutoff frequency found at the level of "−3 dB"?
Why we always take 3 dB down gain of a filter?
Full width at half maximum (FWHM).
Answer: That is the point where the energy (power) is fallen to the value ½ or 0.5 = 50 percent of the initial power as energy quantity, that is equivalent to (−)3 dB = 10×log(0.5). A (−)3 dB power drop is a decrease of 50 % to the value of 50 %.
There the voltage is fallen to the value of √(½) or 0.7071 = 70.71 percent of the initial voltage as field quantity equivalent to (−)3 dB = 20×log(0.7071). A (−)3 dB voltage drop is a decrease of 29.29 % to the value of 70.71 %.
 
(−)3 dB implies ½ the electric power and since the power is proportional to the square of voltage, the value will be 0.7071 or 70.71 % of the passband voltage.
√½ = 1/√2 = √0.5 = 0,7071. P ~ V2, that is 0,5 ~ 0,70712.
 
Sound engineers and sound designers ("ear people") mostly use the usual (sound) field quantity. That'swhy they say:
The cutoff frequency of a device (microphone, amplifier, loudspeaker) is the frequency at which the output voltage level is decreased to a value of (−)3 dB below the input voltage level (0 dB).
● (−)3 dB corresponds to a factor of √½ = 1/√2 = 0.7071, which is 70.71% of the input voltage.
 
Acousticians and sound protectors ("noise fighters") seem to like more the (sound) energy quantity. They tell us:
The cutoff frequency of a device (microphone, amplifier, loudspeaker) is the frequency at which the output power level is decreased to a value of (−)3 dB below the input power level (0 dB).
● (−)3 dB corresponds to a factor of ½ = 0.5, which is 50% of the input power (half the value).
 
Note: Power gain (power amplification) is not common in audio engineering.
Even power amplifiers for loudspeakers don't amplify the power.
They amplify the audio voltage that moves the voice coil.
 
Sound field quantities    AnimatedLaughingSmiley
Sound pressure, sound or particle velocity, particle displacement or displacement amplitude, (voltage, current, electric resistance).
Inverse Distance Law 1/r		         Sound energy quantities
Sound intensity, sound energy density, sound energy, acoustic  power.
(electrical power).
Inverse Square Law 1/r²
 
Note: A sound field quantity (sound pressure p, electric voltage V) is not a sound energy quantity (sound intensity I, sound power Pak). I ~ p2 or P ~ V2. Sometimes you can hear the statement: The cutoff frequency is there where the level L is decreased by (−)3 dB.
Whatever the user wants to tell us so accurately: Level is level or dB is dB.

Bandwidth for Yamaha Parametric Equalizer

For a Yamaha parametric equalizer EQ there is the filter bandwidth of an octave divided in 60/60 (12 semitones).
One half tone step (semitone) is then 5/60 − 01V Digital Mixing Console.
Conversion:
N = "bandwidth in octaves" (semi tone or half tone distance). Q = Q factor
 
Filter EQ N Q Interval        Filter EQ N Q Interval
         5/60      0.083    17.31      Semitone step               95/60      1.583      0.867  
       10/60      0.167      8.651  Whole tone             100/60      1.667      0.819  
       15/60      0.25      5.764               105/60      1.75       0.776  
       20/60      0.333      4.318  1/3 octave             110/60      1.833      0.736  
       25/60      0.417      3.45               115/60      1.917      0.7  
       30/60      0.5      2.871  1/2 octave               120/60      2      0.667  2 octaves
       35/60      0.583      2.456  Fifth             125/60      2.083      0.636       
       40/60      0.667      2.145               130/60      2.167      0.607  
       45/60      0.75      1.902               135/60      2.25      0.581  
       50/60      0.833      1.707               140/60      2.333      0.556  
       55/60      0.917      1.548               145/60      2.417      0.532  
       60/60      1      1.,414  1 octave             150/60      2.5      0.511  2.5 octaves
       65/60      1.083      1.301               155/60      2.583      0.49  
       70/60      1.67        1.204               160/60       2.667      0.471  
       75/60      1.25        1.119               165/60      2.,75      0.453  
       80/60      1.333      1.044               170/60      2.883      0.436  
       85/60      1.417      0.979               175/60      2.917      0.419  
       90/60       1.5      0.92  1.5 octaves             180/60       3      0.404  3 octaves
 
The "BW/60" control replicates the effect of the Behringer Pro DSP1124P - Feedback Destroyer bandwidth setting.
This control sets the bandwidth of the filter between the half-gain points with:
BW (Hz) = f0 × (BW / 60) × √2
For example, at a bandwidth setting of 60/60 a filter centred on 1 kHz with a gain of −6 dB will have a bandwidth of 1,414 Hz between the points where its response crosses −3 dB. This bandwidth remains constant as the filter's gain is adjusted.
Note that the Behringer DSP1100 - 24 band parametric equalizer software package does NOT correctly reproduce the way the bandwidth control actually operates, its bandwidths are too small by a factor of √2.
Defining filter bandwidth in this way is not uncommon (the TMREQ filters use a similar definition).
The relationship between Q and BW for the DSP1124P is:
Q = 60 / [(BW / 60) × √2]
So the bandwidth range of 1/60 to 120/60 gives a range from Q = 42.4 to 0.35.
 
Aha!
At the cut-off frequency fc of a drop the voltage V is always fallen to the value
1/√2 = 0.7071 ≡ 70.71 % and the voltage level is damped by
20 × log (1/√2) = (−)3.0103 dB.

At the cut-off frequency (half-power frequency) the less interesting power P
is always fallen to
1/2 = 0.5 ≡ 50 % and the power level is damped by
10 × log (1/2) = (−)3.0103 dB − that is the same dB value.

This is often confusing. 0.7071 × 0.7071 is 0.5 and P = V²/R; P ~ V².
What do you mean by 3 dB cutoff frequency? Why is it 3 dB, not 1 dB?
Answer: The power P is always fallen there to 1/2 = 0.5 = 50 %.

Quality Factor Q = f0 / BW
BW = f0/Q          Q = f0/BW          f0= BW × Q
 
Please enter two values, the third value will be calculated.

 Center frequency f0  Hz  Quality Factor Triangle
Bandwidth BW  Hz
Quality Factor Q   
Measurement of input impedance and output impedance
 
 
 
back zurück Search Engine weiter home start