| Deutsche Version |  |
 |
| Sound intensity I and the inverse square law 1/r² |
| In the real world, the inverse square law (squared distance law) I ~ 1/r2 is always an
idealization because it assumes exactly equal sound intensity or acoustic intensity I as
sound energy propagation in all directions. If there are reflective surfaces in the sound field,
then reflected sounds will add to the directed sound and you will get more sound intensity at a
field location than the inverse square law predicts. If there are barriers between the source
and the point of measurement, you may get less than the square law predicts. Nevertheless,
the inverse square law is the logical first estimate of the sound intensity you would get at a
distant point in a reasonably open area. The reference sound intensity level SIL = 0 dB is the
acoustic intensity of I0 = 1 pW/m2 = 1 × 10−12 W/m2. Note: Since the sound intensity level (energy size) is difficult to measure, it is common to use sound pressure level (field size) measured in decibels instead. Doubling the sound pressure raises the sound pressure level by 6 dB. Sound pressure in Pa is really not sound intensity in W/m². |
| You can explore numerically to confirm the 1/r2 law that doubling the distance drops the sound intensity I to a quarter (0.25) by a sound intensity level of about (−)6 dB and that 10 times the distance drops the sound intensity I to a hundredth (0.01), that is a level drop by 20 dB. |
 |
|
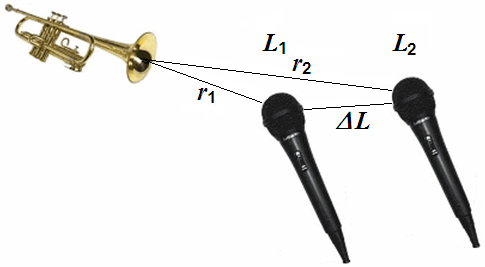Note: The radiated sound power (sound intensity) is the cause and the sound pressure is the effect. The effect is of particular interest to the sound engineer. The effect of temperature and sound pressure: Sound pressure and Sound power – Effect and Cause. |
| Acousticians and sound protectors (noise fighters) need the sound intensity (acoustic intensity). As a sound designer you don't need that sound energy size. The eardrums (tympanic membranes) of our hearing and the diaphragms of the microphones are effectively moved by the sound pressure or the sound pressure level SPL. Who is involved in audio engineering, should care less about the cause of intensity, power and energy, but better care on the effect of the sound pressure and the sound level (sound pressure level SPL) at the eardrums and the microphones, and the corresponding audio voltage or its voltage level. |
Sound pressure and Sound power − Effect and Cause
| Enter a value in the left or right box. The calculator works in both directions of the ↔ sign. |
| Sound intensity level LI: dB-SIL |
↔ | Sound intensity I: W/m2 |
 |
 |
|
| Standard reference sound intensity I0 = 1 pW/m2 = 10−12 W/m2 ≡ 0 dB | ||
 |
|
||||||||||||||||||||||||||||
Calculating sound intensity with the inverse square law
| Relationship of sound intensity I, sound pressure p, and the square law: (r is the distance from the sound source) |
|  |
Formulas for distance attenuation − Sound intensity calculation
| The value of the sound intensity increases inversely squared with increasing distance from the sound source, that means with 1/r2: |
|
|
| Where: | ||
| I1 | = | sound intensity 1 at closer distance r1 from the sound source |
| I2 | = | sound intensity 2 at more far distance r2 from the sound source |
| r1 | = | closer distance r1 from the sound source |
| r2 | = | more far distance r2 from the sound source |
| Note! Since the sound intensity level is difficult to measure, it is common to use sound pressure level measured in decibels instead. Doubling the sound pressure raises the sound pressure level (SPL) by 6 dB. |
| The sound pressure level Lp to plot against the distance of the sound source r 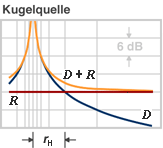 D: direct field of the spheric source R: reflected field (diffuse field) rH: critical distance |
| If we double the distance, the value for the sound pressure falls to a half of its initial value. If we double the distance, the value for the sound intensity falls to a quarter of its initial value. This corresponds to a decrease in level by (−)6 dB. For the level change in dB we get: |
|
|
A doubling of distance from the sound source in the direct field will reduce the "sound level"
by (−)6 dB, no matter whether that are sound intensity levels or sound pressure levels! This
will reduce the sound intensity I (energy size) to 1/22 = 1/4 (25 %) and the sound
pressure p (field size) to 1/2 (50 %) of the the initial value. The inverse square law 1/r2 shows the distance performance of energy sizes and the inverse distance law 1/r shows the distance performance of field sizes. Energy sizes are propotional to squared field sizes – e.g. I ~ p2. |
| Sound Energy sizes Sound intensity, sound energy density, sound energy, acoustic power. (electrical power). Inverse Square Law 1/r² |
Sound Field sizes  Sound pressure, sound or particle velocity, particle displacement or displacement amplitude, (voltage, current, electric resistance). Inverse Distance Law 1/r |
Conversions and Calculations - Sound sizes and their Levels
Frequently used false statements in the context of
sound values and the distance of the sound source
| Wrong expression | Correct version |
| Sound intensity (energy) falls inversely proportional to the distance 1/r from the sound source. wrong |
Sound intensity (energy) falls inversely proportional to the square of the distance 1/r2 from the sound source. |
| Sound intensity level decreases inversely as the square of the distance increases per doubling of sound source with (−)3 dB per doubling. wrong |
Sound intensity level decreases by (−)6 dB per doubling of distance from the source to 1/4 (25 %) of the sound intensity initial value. |
| Sound pressure falls inversely proportional to the square of the distance 1/r2 from the sound source. wrong |
Sound pressure falls inversely proportional to the distance 1/r from the sound source. That is the 1/r law or distance law. |
| Sound pressure level decreases as the distance increases per doubling of distance from the source by (−)3 dB. wrong |
Sound pressure level decreases by (−)6 dB per doubling of distance from the source to 1/2 (50 %) of the sound pressure initial value. |
| Neither the sound power, nor the sound power level decreases in doubling the distance up to a value or up to any dB. Why is this so? |
How many decibels (dB) level change is twice (double, half) or three times as loud?
| Question: How does the sound power decrease with distance"? Answer: "April fool - The sound power does not decrease (drop) with distance from the sound source." The sound power level or the sound power is firmly committed to the sound source and is really independent from the distance. Thinking help: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watt, which is emmited from the bulb all the time! |
 |
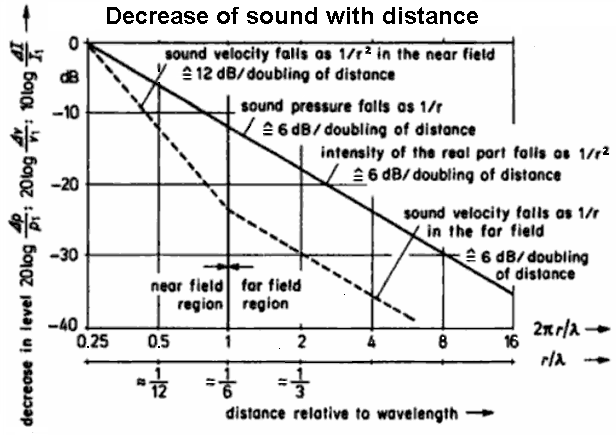| Pressure, velocity, and intensity of the sound field near to and distant from a spherical radiator of the zeroth order |
| "Ear people" like sound engineers and sound designers are mainly
interested in sound field sizes and consider more the sound pressure
drop at distance doubling (Schalldruckabfall - Entfernungsverdopplung). Acousticians and noise fighters are mainly interested in sound energy sizes and consider here the sound intensity drop at distance doubling. They all view together the same line! Isn't that beautiful?Nevertheless, the drop in sound intensity goes with 1/r2 and the decrease of sound pressure is 1/r. This should be understood quite well. I ~ p2. Intensity is proportional to the square of the amplitude. |
| Our hearing (eardrum) is directly sensitive to the sound pressure. From
the historical perspective, the level differences for stereo listening were
called "intensity" differences. However, sound intensity is a specifically
defined size that can not be picked up by a microphone, nor would it be
useful for a sound recording. So call the "intensity" stereophony better
level difference stereophony. If you have to work as a sound technician to check the sound quality by ear, then think of the sound waves, which move the eardrums using the sound pressure as a sound field size. There is also the advice: Avoid the use of sound power and sound intensity as sound energy sizes. |
| How does the sound decrease with distance? |
back  |
Search Engine  |
home  |
1/r²
