RC pad corner frequency upper and lower cutoff frequency calculation filter calculate time constant tau RC voltage power calculator capacitance resistance

● RC Filter and Cutoff frequency ●

Conversion RC-pad
R × C to Corner frequency f_c and Crossover frequency f_c to R × C
Time constant τ (tau) = R × C

f_c = Cut-off frequency = corner frequency = crossover frequency
= half-power frequency = 3 dB frequency = break frequency is all the same.

The 3 dB down point is important because, electrically, two overlapping corner frequency
curves will add up to 0 dB and prevent what appears to be a dip in the frequency response.

The used browser does not support JavaScript.
You will see the program but the function will not work.

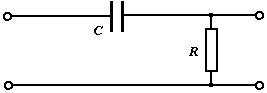	Bass cut - High pass - CR filter: This CR filter rolls off the frequency response at 6 dB per octave below the cutoff frequency. The same calculation applies to both filters. The calculator assumes a low source impedance, which usually is small enough that it does not change the cutoff frequency.
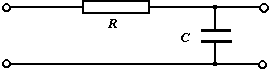	Treble cut - Low pass - RC filter: This RC filter rolls off the frequency response at a ratio of 6 dB per octave above the cutoff frequency (corner frequency). The same calculation applies to both filters.

At the cut-off frequency f_c of a drop the voltage V is always fallen to the value
1/√2 = 0.7071 ≡ 70.71 % and the voltage level is damped by
20 × log₁₀ (1/√2) = (−)3.0103 dB.

At the cut-off frequency (half-power frequency) the
less interesting power P is always fallen to
1/2 = 0.5 ≡ 50 % and the power level is damped by
10 × log₁₀ (1/2) = (−)3.0103 dB – that is the same dB value.

This is often confusing. 0.7071 × 0.7071 is 0.5 and P = V²/R; P ~ V².
What is meant by 3 dB cutoff frequency? Why is it 3 dB, and not 1 dB?
Answer: The power P is always fallen there to 1/2 = 0.5 = 50 %.

RC filter: Resistor R and capacitor C
Search: Corner frequency f_c and time constant τ

Enter the value for resistor and capacitor, then press "calculate".

Bass Cut

Short conditional equations:
f_c in Hz = 159155 / τ in µs
τ in µs = 159155 / f_c in Hz

Treble Cut

The Greek letter for time constant is tau = τ, and 1 microsecond is 10⁻⁶ seconds.
The cutoff frequency is also called corner frequency.
More formulas you find here "Zeitkonstante und Übergangsfrequenz"

Calculating the -3 dB cut-off frequencies f1 and f2 when center frequency f0 and Q factor is given

Frequency response and equalization − Conversion: time constant to cut-off frequency

Low-pass filter? High-pass filter? What does it mean?

For a sound designer (aural architect) it is strange to cut off high frequencies with a low-pass filter and to cut off
low frequencies with a high-pass filter. Filters change the sound in special frequency regions.
Filters changing the low frequencies are application-oriented called low cut filter, bass cut filter, or rumble filter.
Filters changing the high frequencies are better called treble cut filter, high cut filter, or noise filter.

Notice: A low-pass lets pass voltages / amplitudes with low frequencies.
A high-pass lets pass voltages / amplitudes with high frequencies.
These words do not help the practitioners in sound mixing, because it is unimportant, what will theoretically pass through. It is a lot more interesting, what frequencies are practically audibly filtered out (cut off) or added.

Capacitive reactance calculator XC - Reactance of a capacitor

Conversion: Corner frequency to Time constant and vice versa

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Corner angular frequency ω_c = Angular frequency ω_c
The corner angular frequency ω_c is developed from the corner frequency f_c:
ω_c = 2 π ∙ f_c

Upper and Lower Corner frequency f_c = cut-off frequency = crossover frequency
= half-power frequency = 3 dB frequency = break frequency is all the same

For systems that correspond to a differential equation of first Grades the cutoff point is the intersection of the horizontal asymptote with the asymptote of the falling branch of the Bode diagram. At this point, the level is −3 dB and the phase shift is 45°. This means that the amplitude drop of the output value reached 30% of the input size. At the same time the time constant τ of such system is: τ = 1 / ω_c = 1 / 2 π ∙ f_c

At the cutoff frequency f_c the output voltage V₂ = 70.7% of the input voltage V₁, and the output power is P₂ = 50.0% of the input power P₁.

Cut-off frequency to corner angular frequency and vice versa

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Filter Design in Thirty Seconds − Texas Instruments

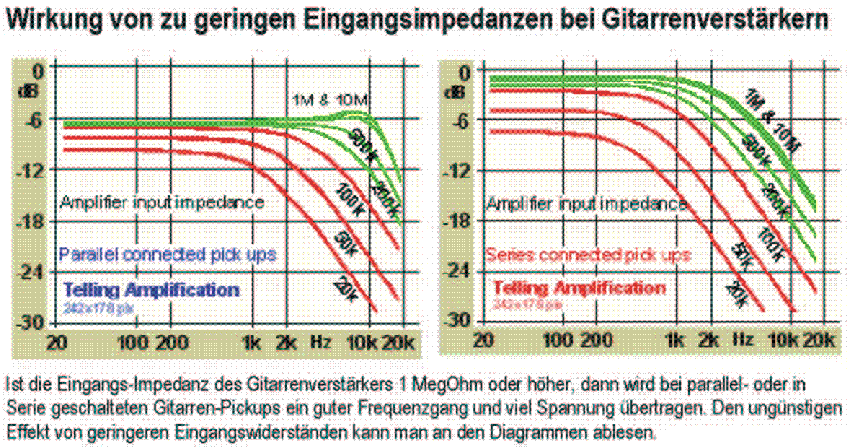
The Input Impedances of Guitar Amplifiers (RC pad)

back

Search Engine

home


Cut-off frequency f_c Hz	↔	Time constant τ µs

1 microsecond = 10⁻⁶second = 0.000001 second


Cut-off frequency f_c Hz	↔	Corner angular frequency ω_c 1/s