Geometric mean formula arithmetic mean calculate find average center frequency difference Hi-Fi phone telephone program two values value harmonic quadratic mean formula - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
Geometric Mean and Arithmetic Mean
 
● Calculation of the geometric mean of two numbers ●
e.g. calculating the center frequency f0 of a bandwidth BW = f2 − f1
 
Comparison between the arithmetic mean (average) and the geometric mean
 
Formula: Difference between arithmetic average and geometric average.
 
You cannot calculate the geometric mean from the arithmetic mean.
 
Enter the numbers f1 and f2 in the boxes, click thecalculation button, and compare the two answers.

 
f1  Hz 
f2  Hz
 
      ↓  
 
 Geometric mean f0  Hz
Arithmetisches Mittel f0  Hz
 
The geometric mean between two numbers (formula): Geo
 
The arithmetic mean between two numbers is: Ari
Example: The cut-off frequencies of a phone line are f1 = 300 Hz
and f2 = 3300 Hz. What is the center frequency?
 
The center frequency is f0 = 995 Hz as geometric mean and not f0 = 1800 Hz as arithmetic mean. What a big difference!

Phone frequencies - logarithmic scale - sengpielaudio
                              f1                           f0                          f2
Telephone transmission range as logarithmic scale. The center frequency is 995 Hz. The
linear distance from 300 Hz to 995 Hz is equal to the linear distance from 995 Hz to 3300 Hz.
The frequency range 300 Hz to 3.3 kHz is the bandwidth of the transmission of 3 kHz.
Sometimes the phone transmission goes even up to 3.4 kHz.

Regenbogenlinie

The HiFi range goes from f1 = 20 Hz to f2 = 20000 Hz. The correct center frequency is f0 = 632.5 Hz (!) as geometric mean and not the value 10.01 kHz of the arithmetic mean calculation. Look here:

Audible frequencies logarithmic scale - sengpielaudio
        f1                                                                               f0                                                                                f2
Audible frequency range with a logarithmic scale. The linear distance from 20 Hz to 632 Hz is equal to the linear distance from 632 Hz to 20 kHz. Look at the marked points in the figure.
 
By defining the center frequency, the ratios of the cut-off frequencies to the
center frequency are the same: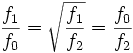
Formula center frequency
 
The geometric mean of two numbers is the square root of their product.
The geometric mean of three numbers is the cubic root of their product.
 The arithmetic mean is the sum of the numbers, divided by the quantity of the numbers.
Other names for arithmetic mean: average, mean, arithmetic average.
 
In general, you can only take the geometric mean of positive numbers.
 
The geometric mean, by definition, is the nth root of the product of the n units in a data
set. For example, the geometric mean of 5, 7, 2, 1 is (5 × 7 × 2 × 1)1/4 = 2.893.
Alternatively, if you log transform each of the individual units the geometric will be the
exponential of the arithmetic mean of these log-transformed values. So, reusing the
example above, exp [ ( ln(5) + ln(7) + ln(2) + ln(1) ) / 4 ] = 2.893.

Geometric Mean
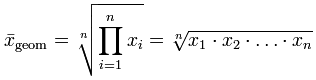
Formeula geometric mean- sengpielaudio

Arithmetic Mean
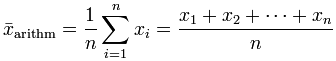
Formula arithmetic mean - sengpielaudio

Calculating the -3 dB cut-off frequencies f1 and f2 when center frequency and Q factor is given.

Geometric mean of more numbers

 
Calculate Geometric Mean
Enter all the numbers separated by comma,
e.g. 300,3000
 


 
Total numbers: 
Geometric mean: 
 
 
Geometric Mean Tutorial
 
Geometric Mean Definition: Geometric Mean is a kind of average of
a set of numbers that is different from the arithmetic average.
The geometric mean is well defined only for sets of positive real numbers.
This is calculated by multiplying all the numbers (call the number of
numbers n), and taking the nth root of the total. A common example of
where the geometric mean is the correct choice - is when averaging
growth rates.
 
Formula: Geometric Mean = ((x1)(x2)(x3) ... (xn))1/n
 
where x = Individual score and n = Sample size (Number of scores)
 
Example to find the Geometric Mean of 1, 2 ,3 ,4 ,5.
 
Step 1: n = 5 is the total number of values. Find 1 / n.
              1 / n = 0.2
 
Step 2: Find Geometric Mean using the formula:
              [(1)(2)(3)(4)(5)]0.2 = 1200.2
              Geometric Mean = 2.60517
 
This example will guide you to calculate the geometric mean manually.
Arithmetic Mean Tutorial
 
Arithmetic Mean Definition: Arithmetic Mean is commonly called as
average. Mean or average is defined as the sum of all the given
elements divided by the total number of elements.
 
Formula: Arithmetic Mean = sum of elements / number of elements
                = a1 + a2 + a3 + ... + an / n
 
Example to find the Arithmetic Mean of 3, 5, 7.
 
Step 1: The sum of the numbers are:
              3 + 5 + 7 = 15
 
Step 2: The total numbers are:
              There are 3 numbers.
 
Step 3: The Arithmetic Mean is:
              15 / 3 = 5
 
 
 
back weiter Search Engine weiter home Start