Sound pressure level SPL 400 particle velocity characteristic specific acoustic impedance Z sound intensity acoustic power sound energy formulas acoustics sound units intensity acoustic characteristic impedance dB SPL calculations pascal audio calculations sound units audio engineering sound recording Acoustic equivalent for ohm's law plane progressive waves - sengpielaudio Sengpiel Berlin

Deutsche Version

Acoustics and Vibrations
● Formulas and Calculations for Sound ●

Relationship of the physical and acoustic quantities (parameters)
Sound pressure p, particle velocity v, specific acoustic impedance of air Z, sound intensity I or J
Pascal Pa, meter per second m/s, newtonsecond / mm³ Ns/m³, watt per m³ W/m³

• Acoustic Equivalent to Ohm's law •
or ohm's law as equivalent in acoustics for
plane progressive waves − Specific acoustic impedance

The particle velocity v is not the speed of sound c = velocity of sound.
Unless otherwise stated, the sound pressure is always meant as RMS value.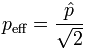
Formula

eff = RMS

Enter any two known values and press "calculate" to solve for the two others. Please, enter only two values.One of these values could be the
specific acoustic impedance or the acoustic impedance of air:
Z₀ = 413 N·s/m³ at 20°C = 68 °F or Z₀ = 410 N·s/m³ at 25 °C = 77 °F.

The used browser does not support JavaScript.
You will see the program but the function will not work.

Principles of the Acoustic Laws and Sound Equations in Analogy (Relationship) to the Ohm's Law. Formulary and Audio Equations

*Formula Wheel*	♥	*Important Formulas*
*of Acoustics + Audio*		*of Sound + Noise*
Acoustical formulas as circle diagram (pie chart)

The Formula Wheel of Acoustics (Audio)

In acoustics and audio engineering sound pressure, air particle velocity, and acoustic impedance are linear sound field quantities. The sound intensity is a quadratic sound energy quantity.

The most important acoustic formulas:
Sound pressure p = Z × v = J / v = √(J × Z) in Pa Particle velocity v = p / Z = J / p = √(J / Z) in m/s
Acoustic impedance Z = p / v = p² / J = J / v² in N·s/m³ Sound intensity J = p × v = Z × v² = p² / Z in W/m²

Specific acoustic impedance Z₀ = ρ × c = p / v in N·s/m³.
The acoustic impedance is a material constant of the propagation medium. Acoustic impedance is the product of the density ρ and the speed of sound c in a medium. As characteristic impedance of air we use the round value Z = 400 N·s/m³ (Pa·s/m). Then the "sound level", that is the sound pressure level and the sound intensity level is exactly the same as a decibel value.
Specific acoustic impedance of air at 20°C is Z₀ = 413 N·s/m³ (Pa·s/m).
Density of air ρ and speed of sound c = λ × f
Sound pressure p = √ (J × Z₀) and sound intensity J = p² / Z₀

The characteristic (acoustic) impedance of a medium is an inherent property of a medium: Z₀= ρ₀ × c₀. Here is the characteristic impedance, measured in Rayls, and ρ₀ and c₀ are the density and speed of sound in the unperturbed medium (i.e. when there are no sound waves travelling in it). In a viscous medium, there will be a phase difference between the pressure and velocity, so the specific acoustic impedance Z will be different from the characteristic acoustic impedance Z₀. The characteristic impedance of air at room temperature is about 400 Pa·s/m or N·s/m³.

See also: The Formula Wheel of Electrical Engineering

Sound pressure p in pascals (newtons per square meter) is not the same physical quantity as intensity J or I in watts per square meter.
... and the sound power (acoustic power) does not decrease with distance r from the sound source - neither with 1 / r nor as 1 / r².

Often the sound pressure as a sound field quantity is mixed incorrectly with the sound intensity as a sound energy quantity.
But I ~ p².
The sound energy quantity is proportional to the sound field quantity squared.

Note: The radiated sound power (sound intensity) is the cause
and the sound pressure is the effect.
The effect is of particular interest to the sound engineers.
The effect of temperature and sound pressure:
Sound pressure and Sound power – Effect and Cause.

Acousticians and sound protectors ("noise fighters") need the sound intensity (acoustic intensity) – but sound engineers and sound designers ("ear people") don't need that sound energy quantity.

Who is involved in audio engineering, should rather take care of the sound field quantity, that is the sound pressure or the sound pressure level (SPL) as an effect at the eardrums of our hearing and on the diaphragms of the microphones, and the corresponding audio voltage and its voltage level.

Sound waves move our eardrums (tympanic membranes).
But which sound quantity produces this effect?

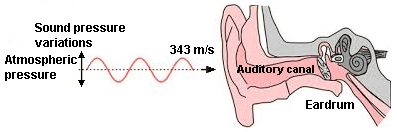Perception of sound

Sound pressure and Sound power – Effect and Cause

Sound power is the cause - but sound pressure produces the audible effect.

The well known law V = I × R means accordingly (equivalent) in the acoustics p = v × Z.

Conversion of acoustic values to sound level L in dBSPL
Many different amplitudes − The sound field quantities of a plane wave
Calculations of sound quantities and their levels
Relationships of acoustic quantites associated with acoustic sound waves
How many decibels (dB) is twice (double, half) or three times as loud?
Ohm's law of the electronics V = I × R
Temperature dependence of physical quantities

Hearing is directly sensitive to sound pressure (eardrums). In stereo the level differences have been called "intensity" differences, but sound intensity is a specifically defined quantity and cannot be sensed by a simple microphone, nor would it be of value in music recordings if it could be.
"Intensity" stereophony is better termed as level difference stereophony, because our eardrums and microphone diaphragms are moved by the differences of the sound pressure level.

Since our ears do not respond to the air particle velocity (sound velocity), but only to the sound pressure changes, the particle velocity is irrelevant on the loudness perception.

Acoustic impedance of a medium = Sound pressure / Particle velocity - Z₀ = p / v

Please enter two values, the third will be calculated. Specific acoustic impedance of air: Z₀ = 400 N·s/m³. Typical assumption.

Acoustic impedance = Density of medium × Speed of sound - Z₀ = ρ (rho) × c

Please enter two values, the third will be calculated. Density of air: ρ (rho) = 1.204 kg/m³ at 20 °C.
Specific acoustic impedance of air: Z₀ = 400 N·s/m³. Typical assumption.
Temperature Dependence of Physical Quantities

Sound intensity = Sound pressure × Particle velocity - J = p × v

Please enter two values, the third will be calculated.

Density of the Medium, Speed of sound, and Acoustic impedance

Medium	Density ρ in kg/m³ at 20 °C	Speed of sound c in m/s at 20 °C	Acoustic impedance Z₀ in N·s/m³
Air	1.204	343	413.5
Water	1,000	1,440	1,440,000
Brick	1,700	4,300	7,310,000
Glass quartz	2,200	5,500	12,100,000
Aluminium	2,700	6,100	16,500,000
Steel	7,500	6,000	45,000,000

In 1970, the pressure reference level of 0 dB ≡ 1 µPa was chosen by the US Navy for their underwater work for sound in water.
Approximately the same level of detail for air and water at their respective reference pressure in level differ by approximately 62 dB.
For a comparability of the levels - anyway in question - withdraw from the sound pressure level under water about 62 dB.
The large difference between the level of sound in air and the indication of the sound level under water specified in decibels (dB) is seldom recognized and clearly explained.

The decrease of sound with distance

How does the volume (loudness) decrease with distance from a sound source?
How does the sound pressure (voltage) decrease with distance from a sound source?
How does the sound intensity (not the sound power) decrease with distance from a sound source? The beginners question is quite simple: How does the sound decrease with distance?

For a spherical wave we get:
The sound pressure level (SPL) decreases with doubling of distance by (−)6 dB.
The sound pressure falls falls to the 1/2 times (50%) of the initial value of the sound pressure.
The sound pressure decreases with the ratio 1/r to the distance.

The sound intensity level decreases with doubling of distance also by (−)6 dB.
The intensity falls to the 1/4 times (25%) of the initial value of the sound intensity.
The sound intensity decreases with the ratio 1/r² to the distance.

The loudness level decreases with doubling of distance also by (−)6 dB.
The loudness falls to the 2/3 times (ca. 63%) of the initial value of the sensed loudness.
The loudness decreases with the ratio 1/(2^0.66r) = 1/1.581 r to the distance.
There was a discussion: 2^−0.6r is not the same thing as 1/(2^0.6)r which shows that
the equation is wrong. But how is it right?

http://en.wikipedia.org/wiki/Wikipedia:Reference_desk/Archives/Science/2009_December_27#Sound_pressure.2C_sound_intensity.2C_sound_loudness.2C_and_decay_with_distance

The sound level depends on the distance between the sound source and the place of measurement, possibly one ear of a subject.
The sound pressure level L_p in dB without the given distance r to the sound source is really useless. Unfortunately this error (unknown distance) is quite often.

What is sound? Sound is a pressure fluctuation in the air. It has the character of a wave motion which is triggered when an air-particle triggers the next. This domino effect is propagated in air at 343 m / s at 20°C as a longitudinal wave. In liquids and solids the speed is significantly higher (water: 1,440 m/s, steel: 6,000 m/s).
Audible sound pressure fluctuations in Pa = pascal are in the range of about 20 µPa = 0 dB (threshold of hearing) up to 150 Pa = 137.5 dB (threshold of pain). The average air pressure of atmosphere at sea level is 101,325 Pa = 1,013.25 hPa.
The number of pressure variations (cycles) per second is called "frequency of sound".
The unit of sound frequency is Hertz (Hz). The audible range for humans is between 20 Hz and 20,000 Hz (20 kHz). High frequencies are perceived louder than low frequencies.
Therefore, in measurements of noise, an A weighting filter is often used (human sense of hearing). When there are very loud and low frequencies, better use a C-weighted filter.
v is defined as the particle velocity with which the vibrating air particles oscillate around their equilibrium position (swing). It is absolutely vital to distinguish between the sound velocity c (speed of sound) and the particle velocity v.

Sound power and sound pressure.
Correlation between sound energy size, and sound field size.
A sound source emits sound power and generates a certain sound. That means:
The sound power is the cause and the sound pressure is the effect.
A comparison of the theory of heat makes the connection clear: The heat radiated by an electric heater makes a certain temperature in the room. How high the temperature will be, depends on room size, type of isolation, the presence of other heat sources and so on.
The power output of the electric heater is always the same, practically independent of the room in which it is located.
The situation is similar with the sound: The sound that we perceive, or a microphone perceives, depends on the distance to the sound source and the acoustic characteristics of the area in which sound waves propagate. In a large, sound-absorbent room a sound source sounds much softer than in a small room with bare concrete walls. But the sound power of the sound source is always the same.
Look at: "Sound pressure and Sound power − Effect and Cause"
http://www.sengpielaudio.com/SoundPressureAndSoundPower.pdf

The sensitivity (transfer factor) in mV / Pa shows clearly that microphones change sound pressure (Pa) to audio voltage (mV).
Energy and power play no role for these microphone transducers.
Our eardrums are also moved by the sound pressure deviations.
Sound pressure as a sound field size cannot be the same like acoustic intensity or sound power as a sound energy size.

[top of page]

Search Engine