

| Deutsche Version |
|
||||||||||||||||||||||
| In acoustics and audio engineering sound pressure, air particle velocity, and acoustic impedance are sound field quantities. The sound intensity is a sound energy quantities. |
| Sound pressure p = Z × v = J / v = √(J × Z) in Pa Particle velocity v = p / Z = J / p = √(J / Z) in m/s Acoustic impedance Z = p / v = J / v2 = p2 / J in N·s/m3 Sound intensity J = p × v = Z × v2 = p2 / Z in W/m2 |
| Specific acoustic impedance Z0 = ρ × c = p / v in N·s/m3. As characteristic impedance of air we use the round value Z0 = 400 N·s/m³. Then the "sound level" as a decibel value is exactly the same of the sound pressure level and the sound intensity level. Conversion: Sound pressure to Sound intensity and vice versa Specific acoustic impedance of air at 20°C is Z0 = 413 N·s/m³. Density of air ρ in kg/m3 Speed of sound c = λ × f in m/s Sound power (acoustical power) Pac = J × A = p × v × A in W Area A = 4π × r2 in m2 Sound intensity J = Pac / A = Pac/ 4π × r2 in W/m2 Particle velocity v = √(E / ρ) in m/s E =Sound energy density Particle displacement ξ = p / (ω × ρ0 × c) in m (RMS) Angular frequency ω = 2π × f Amplitude of sound waves (sound amplitudes) and audio signals |
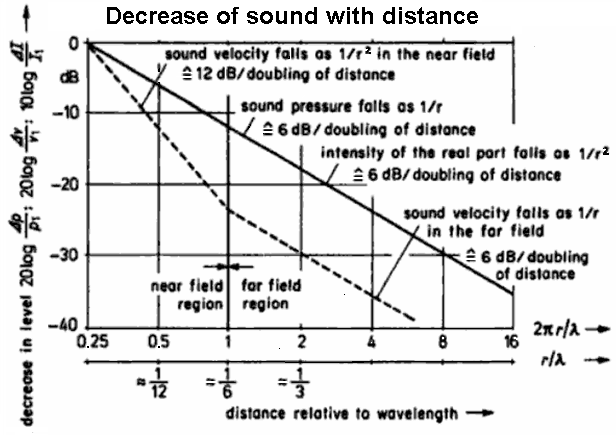 |
| Pressure, velocity, and intensity of the sound field near to and distant from a spherical radiator of the zeroth order |
 |
 |
Sound pressure, Sound intensity and their Levels
| The following calculator shows the often desired direct conversion of sound pressure to sound intensity and vice versa with the specific acoustic impedance of air Z0 = 400 N·s/m3. |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| While the distance dependent sound pressure level in the air is matched with the sound intensity level when a reference sound characteristic impedance Z0 = 400 N·s/m³ is chosen, this is not the case with the distance independent sound power level. |
| Sound pressure and Sound pressure level 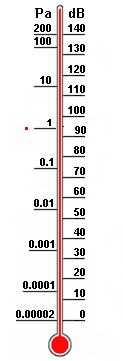 |
|
Sound waves move our eardrums (tympanic membranes).
But which sound quantity produces this effect?
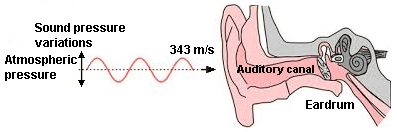 |
|
Sound pressure and Sound power – Effect and Cause Sound power is the cause - but sound pressure produces the audible effect. |
How to measure sound pressure?
 |
| The question: "Is noise level really the sound intensity level?" will be differently
answered by musicians and sound engineers as "ear people" than by
acousticians. We measure the sound of music with a sound level meter (SPL meter) and our eardrums are effectively moved by the sound pressure or its level. A sound engineer thinks that a sound level has mainly to do with the sound pressure deviations. Acousticians as "sound fighters" have a slightly different point of view. They mainly like to calculate the energy (power) of the sound. |
| Neither the sound power Pac nor the sound power level LW decreases when the distance is in
doubled. Why is this so? The sound power level quantifies the totally radiated sound energy from an object. The noise power level is independent of the distance to the object, the surrounding area and other influences. Notice: The psychoacoustic subjective sensations of loudness do not belong to those predictable and measurable sound quantities; see: Correlation between volume level in phone and loudness in sone We feel and judge sound events as: − exposure duration − spectral composition − temporal structure − sound level − information content − subjective mental attitude |
| In sound engineering there is no Power matching or Impedance matching. In audio we use only Voltage bridging or high Impedance bridging. |
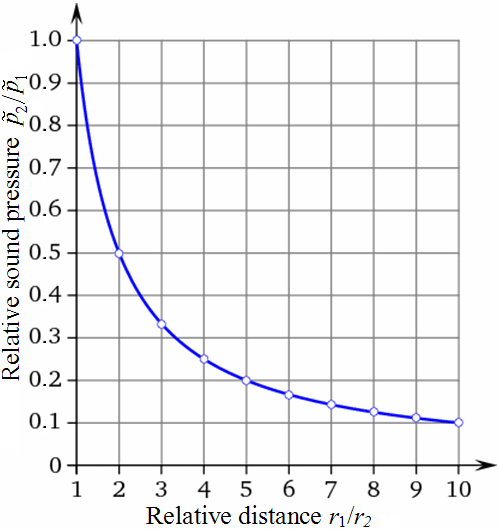
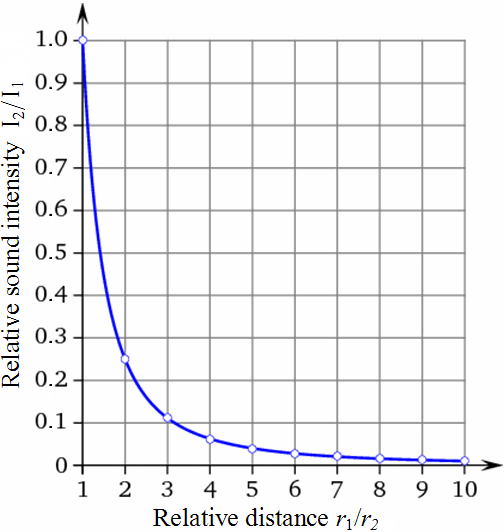
| Differentiate: Sound pressure p is a "sound field size" and sound intensity I is a "sound energy size". In teachings these terms are not often separated sharply enough and sometimes are even set equal. But I ~ p2. |
Changing of sound power with distance is nonsense
| Question: How does the sound power decrease with distance"? Answer: "April fool - The sound power does not decrease (drop) with distance from the sound source." Levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source. Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. A frequent question: "Does the sound power depend on distance?" The clear answer is: "No, not really." We consider sound fields in air which are described by the scalar quantity p (sound pressure) and the vector quantity v (sound velocity) as sound field quantities. |
Acoustic Units of Measurement
| Sound Quantity | Name | Abbreviation | Basic Units | |
| 1) Wavelength λ | metre | m | m | |
| 2) Frequency f | hertz kilohertz |
Hz kHz |
1/s | cycles per second (~) 1 kHz = 1000/s |
| 3) Period T | second millisecond |
s ms |
s | 1 ms = 10−3 s |
| 4) Speed of sound c | metre/second | m/s | m/s | |
| 5) Sound pressure p | pascal micropascal |
Pa = N/m2 µPa |
kg/m·s2 | newton/m2 1 µPa = 10−6 Pa |
| 6) Sound intensity I | watt/m2 | W/m2 | kg/s3 | joule/s·m2 |
| 7) Sound power Pac | watt | W | kg·m2/s3 | joule/s |
Attributes of Sound
| Physical | Perceptual |
| amplitude | loudness |
| frequency | pitch |
| spectrum | timbre |
| duration | length |
| back |
Search Engine |
home |