

| Deutsche Version |
Table (chart): The impact of temperature
The air density, the speed of sound, the characteristic acoustic
impedance and the dependency of the temperature of air
| Temperature of air ϑ in °C |
Speed of sound c in m/s |
Time per 1 m Δ t in ms/m |
Density of air ρ in kg/m3 |
Impedance of air Z0 in N·s/m3 |
| +40 | 354.94 | 2.817 | 1.1272 | 400.0 |
| +35 | 351.96 | 2.840 | 1.1455 | 403.2 |
| +30 | 349.08 | 2.864 | 1.1644 | 406.5 |
| +25 | 346.18 | 2.888 | 1.1839 | 409.4 |
| +20 | 343.22 | 2.912 | 1.2041 | 413.3 |
| +15 | 340.31 | 2.937 | 1.2250 | 416.9 |
| +10 | 337.33 | 2.963 | 1.2466 | 420.5 |
| +5 | 334.33 | 2.990 | 1.2690 | 424.3 |
| ±0 | 331.30 | 3.017 | 1.2920 | 428.0 |
| −5 | 328.24 | 3.044 | 1.3163 | 432.1 |
| −10 | 325.16 | 3.073 | 1.3413 | 436.1 |
| −15 | 322.04 | 3.103 | 1.3673 | 440.3 |
| −20 | 318.89 | 3.134 | 1.3943 | 444.6 |
| −25 | 315.72 | 3.165 | 1.4224 | 449.1 |
ϑ = Temperature, c = Speed of sound, ρ = Density of air, Z0 = ρ × c = Specific acoustic impedance of air
Sound pressure p = √ (I × Z0) and Sound intensity I = p² / Z0 ρ = 101325 / (287.058 × 273.15 + ϑ))
Standard air pressure p0 = 101325 Pa, Specific gas constant R = 287.058 J/kg × K.
| As a reference, the characteristic impedance of the surrounding air (acoustic impedance) is used
with the round value Z0 = 400 N·s/m³ (Pa·s/m) in physics (acoustics) without a temperature responce. Then at this round value the "sound level" as a decibel value, the sound pressure level and sound intensity level coincide exactly. The reference characteristic acoustic impedance Z0 = ρ × c = 400 N·s/m³, is due to the threshold of hearing p0 = 20 Pa (µN/m²) and I0 = 1 pW/m². Sound pressure level and sound intensity level are absolutely identical when the characteristic acoustic impedance is taken as Z0 = 400 N·s/m³. There seem to be some problems with the definition of "characteristic acoustic impedance" and "specific acoustic impedance", and "acoustic impedance". |
| The speed of sound in air is determined by the air itself and is not
dependent upon the amplitude, frequency, or wavelength of the sound. For an ideal gas the speed of sound depends only on its temperature and is independent of gas pressure. This dependence also applies to air, in good approximation and can be regarded as an ideal gas. |
| Notice: The speed of sound changes clearly with temperature, a little bit with humidity − but not with air pressure (atmospheric pressure). The words "sound pressure at sea level" are incorrect and misleading. The temperature indication, however, is absolutely necessary. |
| The average air pressure at sea level is 101325 Pa. However, this information is insignificant for the speed of sound. We always need the specification of the temperature. |
Properties of sound in air
| Simply enter the value to the left or the right side. The calculator works in both directions of the ↔ sign. |
| At 0° Celsius the speed of sound we find in USA books to be 331.3 m/s. At 20° Celsius the speed of sound is then 343.21 m/s, rounded 343 m/s. At 0° Celsius the speed of sound is in German books 331.5 m/s mostly. At 20° Celsius the speed of sound is then 343.42 m/s, rounded 343 m/s. |
The effect of temperature
| The air density is: ρ = p / (R · T) in kg/m3, air pressure = p, gas constant = R, temperature in Kelvin = T The individual gas constant R for dry air is: R = 287.058 J / kg · K with energy joule (J) = newton × meter = N m; T in Kelvin = temperature in °C + 273.15. Atmospheric pressure p0 = 101325 Pa = 1013.25 mbar = 1013.25 hPa und R = 287.058 J/kg · K. With the temperature of T0 = 273.15 K (0 °C) the density of air is: ρ0 = 101325 / (287.058 × 273.15) = 1.2922 kg/m3. For T25 = 298.15 K (25°C) (Normal conditions) the density of air is: ρ25 = 101325 / (287.058 × 298.15) = 1.184 kg/m3. Furthermore it is customary T20 = 293.15 K ↔ 20°C and the density of air is ρ = 1.204 kg/m3. As you see, this sizes are strongly temperature dependent. The speed of sound in air is: 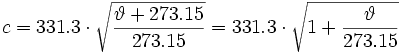 ϑ (theta) is the temperature in degrees Celsius. Z0 = ρ0 × c Z0 is the specific acoustic impedance of air and c is the speed of sound. In SI units with dry air at 20°C (68°F), the speed of sound c is 343 m/s. This also equates to 1235 km/h, 767 mph, 1125 feet per second (ft/s), or 666 knots. |
| Google is not correct (look at the following link) http://productforums.google.com/forum/#!category-topic/websearch/unexpected-search-results/N5JMdZOkeuQ Here is the wrong answer of Google: "Speed of sound at sea level = 340.29 m/s". This is not a good answer, because they forgot to tell us the important temperature, and the given atmospheric pressure "at sea level" makes really no sense. |
| Reason: The static air pressure p_ and density ρ of the air at the same temperature are proportional to each other. The ratio p / ρ is always constant, on a high mountain or even at sea level. Atmospheric pressure p_ and density of air ρ go always together. The ratio stays constant. When calculating the speed of sound, forget the atmospheric pressure, but regard the important temperature. The speed of sound varies with altitude (height) only because of the changing temperature! |
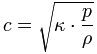 |
| Adiabatic index or ratio of specific heats κ (kappa) = cp / cv. Generally we take with sufficient accuracy the formula (equation) for the speed of sound in air in m/s vs. temperature ϑ (theta) in degrees Celsius (centigrade):
That gives e.g. at ϑ = 20°C a speed of sound c = 331 + (0.6 × 20) = 343 m/s.
|
| That gives e.g. at ϑ = 20°C the speed of sound c = 331.3 + 0.606 × 20 = 343.42 m/s. Often the easy calculation will do: c ≈ 331 + (0.6 × 20) = 343 m/s.
There is a useful formula (rule of thumb) to get the temperature ϑ (°C) when you know the speed of sound c in air (m/s). Formula: Temperature of air ϑ ≈ (c − 331.5) / 0.606 in °C. With the following formula you can calculate more exactly the speed of sound. Speed of sound 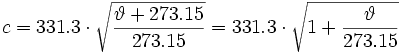 in m/s and temperature ϑ in °C. Temperature of air ϑ°C = 273.15 × (0.000009110812904081 × c² − 1) in °C. Speed of sound c = 331.3 × sqrt (1+(ϑ°C / 273.15)) |
Calculation and conversion: Speed of sound and air temperature
| Simply enter the value to the left or the right side. The calculator works in both directions of the ↔ sign. |
| Note: The radiated sound power (sound intensity) is the cause - and the sound pressure is the effect. The effect is of particular interest to the sound engineer. The effect of temperature and sound pressure. |
| Acousticians and sound protectors ("noise fighters") need the sound intensity (acoustic intensity) – but sound engineers and sound designers ("ear people") don't need that sound energy quantity. Who is involved in audio engineering, should rather take care of the sound field quantity, that is the sound pressure or the sound pressure level (SPL) as an effect at the eardrums of our hearing and on the diaphragms of the microphones, and the corresponding audio voltage and its voltage level. |
Sound pressure and Sound power − Effect and Cause
Converter: Fahrenheit to Celsius and Celsius to Fahrenheit
| Simply enter the value to the left or the right side. The calculator works in both directions of the ↔ sign. |
| From Celsius to x degrees | From x degrees to Celsius | |
| Fahrenheit | °F = °C × 9/5 + 32 | °C = (°F − 32) × 5/9 |
| Kelvin | K = °C + 273.15 | °C = K − 273.15 |
| Rankine | °R = (°C + 273.15) × 9/5 | °C = (°R − 491.67) × 5/9 |
| Delisle | °De = (100 − °C) × 3/2 | °C = 100 − °De × 2/3 |
| Newton | °N = °C × 33/100 | °C = °N × 100/33 |
| Réaumur | °Ré = °C × 4/5 | °C = °Ré × 5/4 |
| Rømer | °Rø = °C × 21/40 + 7.5 | °C = (°Rø − 7.5) × 40/21 |
| From Fahrenheit to x degrees | From x degrees to Fahrenheit | |
| Celsius | °C = (°F − 32) × 5/9 | °F = °C × 9/5 + 32 |
| Kelvin | K = (°F + 459.67) × 5/9 | °F = K × 9/5 − 459.67 |
| Rankine | °R = °F + 459.67 | °F = °R − 459.67 |
| Delisle | °De = (212 − °F) × 5/6 | °F = 212 − °De × 6/5 |
| Newton | °N = (°F − 32) × 11/60 | °F = °N × 60/11 + 32 |
| Réaumur | °Ré = (°F − 32) × 4/9 | °F = °Ré × 9/4 + 32 |
| Rømer | °Rø = (°F − 32) × 7/24 + 7.5 | °F = (°Rø − 7.5) × 24/7 + 32 |
|
| The question of the exact speed of sound can not be answered. It always needs an indication of the temperature and humidity, but not the air pressure. The term speed of sound above "sea level" (Mean Sea Level MSL) is here of no use, because only the temperature is significant and not the height above sea level. |
Density of water ρ (rho) (pure and airfree)
at standard air pressure p0 = 101325 Pa.
Temperature between 0°C and 100°C
| Temperature (°C) - ρ (kg/m³) | Temperature (°C) - ρ (kg/m³) | 0 918.00 (ice) 0 999.84 1 999.90 2 999.94 3 999.96 4 999.97 ● 5 999.96 6 999.94 7 999.90 8 999.85 9 999.78 10 999.70 11 999.60 12 999.50 13 999.38 14 999.24 15 999.10 16 998.94 17 998.77 18 998.59 19 998.40 20 998.20 21 997.99 22 997.77 23 997.54 24 997.29 25 997.04 |
26 996.78 27 996.51 28 996.23 29 995.94 30 995.64 31 995.34 32 995.02 33 994.70 34 994.37 35 994.03 36 993.68 37 993.32 38 992.96 39 992.59 40 992.21 45 990.21 50 988.03 55 985.69 60 983.19 65 980.55 70 977.76 75 974.84 80 971.79 85 968.61 90 965.30 95 961.88 100 958.35 water vapour 101325 Pa: 100 0.5 |
| The dependence of the pressure on the water density is low. Per 1 bar = 100000 Pa pressure increase, the density increases to about 0.046 kg/m³. Therefore normal air pressure fluctuations have practically no influence on the density of water. |
| back |
Search Engine |
home |