

| English version |
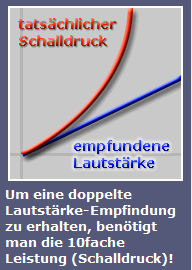
| Das ist keine Fangfrage. Hier wird nicht nach der subjektiv vom Gehör empfundenen Laut- stärke gefragt und nicht wie sich Schallquellen addieren. SPL ist auch nicht ominös, sondern ist die Abkürzung für das englische "Sound Pressure Level", was übersetzt einfach Schalldruckpegel heißt. Der Begriff Lautsprecher und auch Verstärkerleistung ist mit der obigen Umfrage deutlich nicht angesprochen. Es geht nur um objektiven Schalldruck. Die Antwort ist eindeutig: Der doppelte Schalldruck ist als Pegel +6 dB. Man sollte jetzt weiterlesen, wenn man hiermit nicht klarkommt und etwas mehr wissen will. |
| Subjektiv empfundene Lautstärke (Lautheit), objektiv gemessener Schalldruck (Spannung) und theoretisch berechnete Schallintensität (Schallleistung) |
| Hier gibt es die Schallpegel-Abhängigkeit in dB, die entsprechenden Faktoren und die Bewertung von Messungen und persönlichen Empfindungen. |
| Das ist nicht einfach zu verstehen: Da gibt es die "gefühlte" Lautstärke und den künstlichen Begriff Lautheit und die an einem Mikrofon zu messende Tonspannung (Audiospannung) mit dem dazu proportionalen Schalldruck und der zu errechnenden Schallintensitätbzw. der Schallleistung. Wie viel dB ist denn zweimal (doppelt, halb) oder dreimal so lauter Schall? Wie ist die Abhängigkeit vom Pegel oder wie ist die Pegelabhängigkeit in dB? Ist mit dem üblichen Wort "Schallpegel" eigentlich der Lautstärkepegel, der Lautheitspegel, der Schalldruckpegel, der damit proportionale Spannungspegel, der Schallintensitätspegel, der Schallleistungspegel, der Schallenergiedichtepegel oder gar der A-bewertete oder der C-bewertete Schallpegel gemeint? Es geht hier um die Pegeldynamik der Amplituden. Vermeide den amateurhaften Begriff Schallstärke. |
| Der Mensch empfindet und beurteilt Schallereignisse nach: Einwirkungsdauer, spektraler
Zusammensetzung, zeitlicher Struktur, Schallpegel, Informationsgehalt und subjektiver Einstellung. Drei physikalisch messbare Kenngrößen (Parameter) lassen sich an musikalischem Material feststellen und getrennt voneinander beschreiben. Die Tonhöhe (beziehungsweise die Grundfrequenz f ), die Tondauer (beziehungsweise das Zeitintervall Δ t) und der Schalldruck (beziehungsweise die Amplitude y0). Manchmal wird auch die Klangfarbe (beziehungsweise das akustische Spektrum) zu den Parametern gezählt; jedoch lässt sich "Klangfarbe" nur im übertragenen Sinne als Parameter bezeichnen, denn sie besteht nicht aus einer Variablen mit diskretem Wert. Niemals zu vergessen ist die Änderung der Lautstärke mit dem Abstand zur Schallquelle. Eine typische Frage: "Wie viel mehr intensiv (lauter) ist ein 18 dB Schall im Vergleich zu einem 6 dB Schall?" Der Pegelunterschied beträgt 18 dB minus 6 dB = 12 dB? Der Rechner gibt Antworten: 12 dB Pegeldifferenz entspricht einem Schallintensitätsfaktor von 15,85 oder einem Schalldruckfaktor von 3,98, oder einem Lautheitsfaktor 2,3. Ist eigentlich klar, was Intensität bedeutet? Wird wirklich genau die Intensität gebraucht? Verdoppelte Lautstärke ist wie viel dB? Wirklich Lautstärke? |
| Vermeide die Verwendung der psychoakustischen Ausdrücke Lautstärke und Lautheit. Diese subjektive Schall-Empfindung ist nicht eindeutig messbar. Die Begriffe "Lautstärke" oder "Lautheit" sind ein Problem, weil diese zur Psycho- Akustik gehören und solch eine persönliche Empfindung nicht klar bestimmbar ist. Lautheit oder Lautstärke wird als psychologische Ergänzung der physischen Schall- Stärke (Amplitude) auch nach anderen Parametern als dem Schalldruck beurteilt, einschließlich der Frequenz, der Bandbreite, der spektralen Zusammensetzung, dem Informationsgehalt, der zeitlichen Struktur, der subjektiven Einstellung, sowie der Einwirkungsdauer des Schallsignals. Der gleiche Schall erzeugt nicht bei allen Individuen (Menschen) die gleiche Lautheitsempfindung. |
| Als psychoakustische Größen zur Beschreibung der "Lautstärke" gibt es den "Lautstärkepegel" (Lautheitspegel) LN mit der Einheit Phon und die "Lautheit" N mit der Einheit Sone. |
Pegel in Dezibel (dB) und ihre unterschiedlichen Faktoren
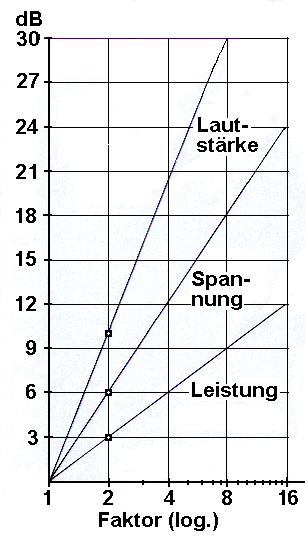 |
| Doppelte Lautheit = Faktor 2 ist etwa 10 dB mehr empfundener Lautstärkepegel (Psychoakustik) Doppelte Spannung = Faktor 2 ist 6 dB mehr gemessener Spannungspegel (Schalldruckpegel) ● Doppelte Leistung = Faktor 2 ist 3 dB mehr berechneter Leistungspegel (Schallintensitätspegel) |
| Während 6 dB SPL eine Verdopplung der Amplitude darstellt, ist eine nicht exakte Daumen-Regel, dass jede 10-dB-Erhöhung eine Verdoppelung der wahrgenommenen "Lautstärke" oder "Lautheit" darstellen soll - sagen uns die Psycho-Akustiker. Nicht den Satz verwenden: "Verdoppeln von Dezibel, or Verdoppeln von dB". Immer wird der Faktor verdoppelt. |
Schallpegeländerung und Lautheitsfaktor
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beiden Richtungen des ↔ Zeichens. |
| Bei Dezimal-Eingabe ist der Punkt zu verwenden. Lautstärke ist nicht das gleiche wie Intensität! Aha! Der Faktor ist in der Mathematik ein Teil eines Produkts. Ein Faktor gibt das x-fache einer Grundmenge an. Die Amplitude der Schallwelle ist die Änderung des Schalldrucks (Effektivwert), wenn die Welle vorbeizieht. |
| "Lautstärke" kann nicht das gleiche sein wie "Intensität" und
"Schallintensität" ist nicht das gleiche wie "Schalldruck". Die Begriffe Lautstärke, Schalldruck und (Schall)-Intensität sind sorgfältig auseinanderzuhalten. Und was ist eine Amplitude? |
| Wer Schallschwingungen praktischerweise mit den Trommelfellen unseres
Gehörs und mit Mikrofonen beschreibt, also einfach hört, der sollte sich
unbedingt um die Wirkung des Schalls kümmern und dazu als Schallfeldgröße
den Schalldruck als schnelle Luftdruckschwankung betrachten. Die Schallenergiegrößen, wie Schallleistung und Schallintensität haben hierbei wenig zu suchen und führen üblicherweise in die Irre. Nutzschall ist eine für das Ohr angenehme Luftdruckschwankung, während man unter Störschall z. B. den ungewünschten Straßenverkehrslärm versteht. |
Zweifacher, doppelter Schall, also eine Verdopplung . . .
Welcher Schall denn?
| Verdopplung der Lautstärke (Lautheit) soll bei einer Pegeländerung von etwa +10 dB empfunden werden. Verdopplung beim Schalldruck (Spannung) entspricht der gemessenen Pegeländerung von +6 dB ● Verdopplung bei der Schallintensität (Schallenergie) entspricht der berechneten Pegeländerung von +3 dB. +10 dB ist der Pegel der zweifach wahrgenommenen Lautstärke in der Psychoakustik − ungefähr empfunden. +6 dB ist der Pegel vom zweifachen (Effektiv-)Wert der Spannung bzw. dem Schalldruck − hauptsächlich gemessen ● +3 dB ist der Pegel als zweifache Energie , also der Leistung (Power) bzw. der Intensität − überwiegend berechnet. Bei Spannung und Schalldruck wird in der Akustik üblicherweise der gemessene Effektivwert angegeben. Bei sinusförmigen Wechselsignalen wird der Scheitelwert U0 oder p0 mit Amplitude bezeichnet. Ueff = | U0 | / √ (2). Bei mehreren Maximalwerten innerhalb einer Periode heißt der größte Wert Spitzenwert. |
|
| 20 dB Pegeländerung sollen den Faktor 4 (vierfach) bei der empfundenen Lautstärke und Lautheit ergeben, 20 dB Pegeländerung ergeben den Faktor 10 bei der gemessenen Spannung und dem Schalldruck und 20 dB Pegeländerung ergeben den Faktor 100 bei der berechneten Schallleistung und der Schallintensität. |
| In den Newsgroups werden diese häufig unverstandenen Aussagen eher weniger korrekt erklärt. Für Dezibel dB ist hier auch dBSPL oder dBA zu nehmen; dabei ist eine Pegeländerung immer in dB. Die empfundene Lautstärke des Schalls hängt von mehreren Faktoren ab: Von der Amplitude, also vom Schalldruckpegel, von der Frequenz, sowie vom Zeitverhalten des Schalls. Eine typische Frage im Internet: "Sind 3 dB oder 6 dB die doppelte Lautstärke?" Antwort: "Es sind weder 3 dB noch 6 dB − eher sind es 10 dB." |
Das menschliche Lautstärke-Empfinden
Schallpegel-Vergleichstabelle und der Faktor
| Die Schallpegelabhängigkeit und die dazugehörende Änderung des Faktors bei subjektiver
Lautstärke (Lautheit), objektivem Schalldruck (Spannung) und der Schallintensität (Leistung) Wie viel Dezibel (dB) Pegeländerung ist zweimal, halb oder gar viermal so laut? Wie viel dB werden doppelt so laut empfunden (zweifach)? Hier sind die unterschiedlichen Faktoren. Faktor bedeutet "das Wievielfache", also "wie oft" ... Verdopplung der Lautstärke. |
| Pegel- Änderung |
Lautstärke Lautheit |
Spannung Schalldruck |
Schallleistung Schallintensität |
| +60 dB | 64 | 1000 | 1000000 |
| +50 dB | 32 | 316 | 100000 |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31,6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2,0 = Verdopplung | 3,16 = √10 | 10 |
| +6 dB | 1,52 fach | 2,0 = Verdopplung | 4,0 |
| +3 dB | 1,23 fach | 1,414 fach = √2 | 2,0 = Verdopplung |
| - - - - ±0 dB - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - |
| −3 dB | 0,816 fach | 0,707 fach | 0,5 = Halbierung |
| −6 dB | 0,660 fach | 0,5 = Halbierung | 0,25 |
| −10 dB | 0,5 = Halbierung | 0,316 | 0,1 |
| −20 dB | 0,25 | 0,100 | 0,01 |
| −30 dB | 0,125 | 0,0316 | 0,001 |
| −40 dB | 0,0625 | 0,0100 | 0,0001 |
| −50 dB | 0,0312 | 0,0032 | 0,00001 |
| −60 dB | 0,0156 | 0,001 | 0,000001 |
| Log. Größe | Psychogröße | Feldgröße | Energiegröße |
| dB- Änderung |
Lautstärke- faktor |
Amplituden- faktor (Effektivwert) |
Leistungs- faktor |
| Verhältnis / Faktor |
Änderung Schall- lautheitspegel |
Änderung Schall- |
Änderung Schall- leistungspegel |
| 40 | +53,22 dB | +32,04 dB | +16,02 dB |
| 30 | +49,07 dB | +29,54 dB | +14,77 dB |
| 20 | +43,22 dB | +26,02 dB | +13,02 dB |
| 15 | +39,07 dB | +23,52 dB | +11,76 dB |
| 10 | +33,22 dB | +20 dB | +10 dB |
| 5 | +23,22 dB | +13,98 dB | +6,99 dB |
| 4 | +20 dB | +12,04 dB | +6,02 dB |
| 3 | +15,58 dB | +9,54 dB | +4,77 dB |
| 2 | +10 dB | +6,02 dB | +3,01 dB |
| - - - - - 1 - - - - - | - - - - ±0 dB - - -- - | - - - - ±0 dB - - - -- | - - - - ±0 dB - - -- - |
| 1/2 = 0,5 | −10 dB | −6,02 dB | −3,01 dB |
| 1/3 = 0,3333 | −15,58 dB | −9,54 dB | −4,77 dB |
| 1/4 = 0,25 | −20 dB | −12,04 dB | −6,02 dB |
| 1/5 = 0,2 | −23,22 dB | −13,98 dB | −6,99 dB |
| 1/10 = 0,1 | −33,22 dB | −20 dB | −10 dB |
| 1/15 = 0,0667 | −39,07 dB | −23,52 dB | −11,76 dB |
| 1/20 = 0,05 | −43,22 dB | −26,02 dB | −13,02 dB |
| 1/30 = 0,033 | −49,07 dB | −29,54 dB | −14,77 dB |
| 1/40 = 0,025 | −53,22 dB | −32,04 dB | −16,02 dB |
| Der Lautheits-Faktor 4 (viermal so laut) ändert den Schall-Lautheitspegel um 20 dB dB. Der Schalldruck-Faktor 4 (der vierfache Schalldruck) ändert den Schalldruckpegel um 12,04 dB dB. Der Schallleistungs-Faktor 4 (vierfache Intensität) ändert den Schall-Leistungspegel um 6,02 dB. |
| Der Lautheits-Faktor 3 (dreimal so laut) ändert den Schall-Lautheitspegel um 15,58 dB. Der Schalldruck-Faktor 3 (der dreifache Schalldruck) ändert den Schalldruckpegel um 9,54 dB. Der Schallleistungs-Faktor 3 (dreifache Intensität) ändert den Schall-Leistungspegel um 4,77 dB. |
| Der Lautheits-Faktor 2 (zweimal so laut) ändert den Schall-Lautheitspegel um 10 dB. Der Schalldruck-Faktor 2 (der zweifache Schalldruck) ändert den Schalldruckpegel um 6,02 dB. Der Schallleistungs-Faktor 2 (zweifache Intensität) ändert den Schall-Leistungspegel um 3,01 dB. |
| Das Hören als akustische Wahrnehmung ist eine rein subjektive Erfahrung. Die Lautstärke oder die Lautheit ist als gehörter Schall und psychologischer Begriff nur subjektiv zu empfinden. Sie wird durch seine Amplitude dargestellt, genauer durch den Effektivwert der Schalldruckamplitude. Das subjektiv empfundene Gefühl wird oft mit objektiven Schalldruckpegelmessungen in Dezibel verwechselt. Mit dem physikalischen Begriff Schallpegel meinen wir üblicherweise ein logarithmisches Verhältnis des messbaren Schalldrucks. Das Verhältnis der Einheit sone zu einem phon wurde so gewählt, dass eine Verdoppelung der Zahl der sone dem menschlichen Ohr vorkommt, wie eine Verdopplung der Lautstärke, die auch der Erhöhung des Schalldrucks um (+)10 dB, oder der Erhöhung des Schalldrucks um den Faktor 3,16 = Wurzel aus 10 entspricht. Lautstärke ist als musikalischer Parameter recht emotional besetzt und wird daher in der ästhetischen Diskussion häufig konträr und missverständlich dargestellt. Lautstärke wird in einem tiefsitzenden archaischen Sinn mit Größe und Macht assoziiert. Kritik an der Lautstärke von Musik − vor allem von Musik aus Lautsprechern - kann daher ein unausgesprochenes ästhetisches Urteil beinhalten: "Was mir gefällt, was ich respektiere, darf schon etwas lauter sein, was ich nicht respektiere hat gefälligst leise und verhalten zu sein." Also: Weg mit dem Rap. "Zusammenhang zwischen Sone und Phon": http://www.sengpielaudio.com/RechnerSonephon.htm |
Lautstärke - Schalldruck - Intensität
Die Faktoren und ihre Pegel in Dezibel (dB).
|
| Aus: http://www.bv-elbtal.de/html/was_ist_larm_.html |
Lautstärke - Schalldruck - Intensität
Unterschiedliche Weinsorten. Der mittlere Wein mundet weitaus am besten.
"Lautstärke" sollte nie mit "Intensität" verwechselt oder gleichgesetzt werden.
|
| Zusammenhang zwischen sone und phon (Psychoakustik)
Umrechnung der Schallgrößen (Pegel) Summen-Pegelberechnung |
Die oft unbekannten Formeln für den Pegel und den Faktor (Ratio)
Lautstärke-Formel - Druck-Formel - Intensitäts-Formel
| Psychoakustik − Pegeländerung Lautstärke 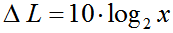 |
Faktor für "Lautstärke" |
| Feldgröße − Pegeländerung Schalldruck 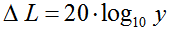 |
Faktor für "Schalldruck" |
| Energiegröße − Pegeländerung Schallintensität 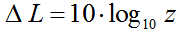 |
Faktor für "Schallintensität" |
log zur Basis 10 = log10 wird auch mit lg bezeichnet.
log zur Basis 2 = log2 wird auch ld = logarithmus dualis genannt.
Logarithmus zur Basis 2, auch Zweierlogarithmus, dyadischer oder binärer Logarithmus.
Δ L = (10/log10(2))·log(x) = 33,22·log (x) = 10·log2(x) x = 10(ΔL/33,22) = 2(ΔL/10)
| Eine typische Frage: Wie viel dB mehr sind denn die 3-fache subjektive Lautstärke? Einige Menschen haben Probleme mit der Vorstellung von "doppelt so laut", oder "dreimal so laut". Ich oute mich − ich gehöre auch dazu. Jedenfalls sagt uns die Lösung des obersten Rechners: 15,85 dB. Hm... Die psychoakustischen Werte der Lautstärke (Lautheit) sind immer signal-, impuls- und frequenzabhängig. Daher ist eine Aussage über diese gefühlte Empfindungsgröße mit einer gewissen Zurückhaltung zu betrachten. |
|  |
| Merke: "Lautheit ist ein künstlicher Begriff (engl. loudness) aus der
Psychoakustik, dem in der Umgangssprache die Lautstärke entspricht". Der Begriff Lautheit wurde erst 1936 von Stanley Smith Stevens mit dem Fachbegriff "Sone" und loudness als "Lautheit" von den Psychoakustikern bei uns eingeführt. |
| Der normale Mensch kennt nur Lautstärke und hat ein etwas komisches Gefühl bei dem Wort Lautheit. |
| Dieser nicht auszuhaltende Satz wurde unter dem Begriff "Lautheit" von
einem ordentlichen Administrator aus Wikipedia beseitigt. Darum steht dieser unerwünschte, also störende Satz jetzt unlöschbar hier. |
| Eine falsche Meinung: "Ein 43 dB lautes Geräusch, das etwa einer
normalen Unterhaltung entspricht, ist doppelt so laut wie ein Geräusch
von 40 dB." Anstatt 40 dB muss es 33 dB heißen. Da von Lautstärke gesprochen wird, ist hier der psychoakustische Pegelwert von etwa 10 dB als Verdopplung der Lautstärke anzunehmen. Eine richtige Meinung: Ein Geräusch mit dem gemessenen Schalldruck- pegel von 40 dB und ein anderes Geräusch mit dem gemessenen Pegel von 40 dB ergeben zusammen einen gemessenen Gesamt-Schalldruck- pegel von 43 dB. Anmerkung: Der Begriff der Verdopplung oder Halbierung einer Lautheit ist zumindest recht schwammig. Wer weiß schon wirklich genau, wann ein Ton halb so laut ist? Das entspricht dem unmöglich genauen Urteil wann eine Tasse Kaffee halb so heiß empfunden wird. Darum sollte diese theoretische Lehre mit etwas Zurückhaltung betrachtet werden. Die Bewertung der "halben" Lautstärke gehört eben zur Psychoakustik. |
Auto-Freaks und "dB Drag Racing" Fans brauchen für ihre "Boxen":
![]() Die großen Leistungsformeln
Die großen Leistungsformeln
oder zeitgemäßer ausgedrückt "Die Mega Power-Formeln"
![]()
Die psycho-akustische Lautstärke bzw. die
Lautheit ist eine subjektive Empfindungsgröße
| Ist 10 dB oder 6 dB Schallpegeländerung eine Verdopplung oder Halbierung der Lautstärke?
Über den Zusammenhang zwischen Schallpegel und Lautheit gibt es verschiedene Theorien. Weit
verbreitet ist immer noch die Theorie des Psychoakustik-Pioniers Stanley Smith Stevens, der angibt,
dass die doppelte oder die halbe Lautheitsempfindung einer Pegeldifferenz von 10 dB entspricht. Neuere Untersuchungen von Richard M. Warren führen dabei zu einer Pegeldifferenz von 6 dB. *) Das heißt, dass doppelter Schalldruck einer doppelten Lautheit entspricht. Der Psychologe John G. Neuhoff fand heraus, dass das Gehör für ansteigende Pegel empfindlicher ist als für abfallende Pegel. Bei gleicher Pegeldifferenz ist die Lautheitsänderung von leise nach laut stärker als von laut nach leise. Die derzeitige Skala der Lautheit in sone stellt somit keine grundlegende Beziehung zwischen Reiz und Empfindung dar. *) Richard M. Warren, "Elimination of Biases in Loudness Judgments for Tones", 1970, Journal of the Acoust. Soc. Am. Volume 48, Issue 6B, pp. 1397 - 1403 and Richard M. Warren, "Quantification of Loudness", 1973, American Journal of Psychology, Vol 86 (4), pp. 807 - 825 John G. Neuhoff, "An adaptive bias in the perception of looming auditory motion", 2001, Ecological Psychology 13 (2) pp. 87 - 110 and John G. Neuhoff, "Perceptual Bias for Rising Tones", 1998, Nature, Volume 395, 10 September Zitat: When known experimental biases were eliminated, half loudness was equal to half sound pressure level (−6 dB) from 45 to 90 dB. Übersetzung: Wenn die bekannten experimentellen systematischen Fehler beseitigt wurden, dann war die halbe Lautheit gleich dem Schalldruckpegel von (−6 dB) bei einem Pegel von 45 bis 90 dB. Hieraus folgt, dass die Bestimmung der doppelten Lautstärke (Lautheit) nicht wie bisher hart dogmatisch festgelegt werden sollte. Wirklichkeitsnäher ist die Angabe: |
| Eine empfundene Verdopplung der Lautstärke entspricht etwa einer Pegeländerung des Schalls zwischen 6 dB und 10 dB. |
| ... Übrigens: Man kann keine "Pegel" sinnvoll verdoppeln oder vervielfachen. Es gibt doppelte Spannung und doppelten Schalldruck. Was ist doppelter Pegel? 3 dB, 6 dB oder 10 dB? Aha - daher sollte man besser diesen Ausdruck vermeiden. Am Ausgang liegt der "doppelte Pegel" meint nachlässig, dass dort die doppelte Spannung liegt. Der Ausdruck: "Der doppelte Pegel ist +3 dB" ist wirklich Unsinn. Was ist das Verdoppeln von 10 Dezibel? Das ist keine gute Frage. |
| Typische Frage? Ist 3 Dezibel mehr Pegel doppelt so laut? Antwort: Nein! Psychoakustiker meinen, dass wireine Pegeleerhöhung zwischen 6 und 10 dB etwa als "doppelt" so laut empfinden. |
Pegeldynamik (Amplitudendynamik) und
Spektraldynamik (Klangfarbendynamik)
| Eine ebenso große Bedeutung wie die Pegeldynamik hat die Klangfarbendynamik, die auch Spektraldynamik genannt wird. Die empfundene Lautstärke wird fast unabhängig vom Amplituden-Pegel auch durch ein spezifisches Klangfarbenspektrum der von Musikinstrumenten gespielten Dynamikstufen charakterisiert. |
| Eine recht gut gemachte Webseite zum Thema: "Schluss mit Lärm": http://www.jwsl.de/bonus/sml/fakten/c2-20.php?mainlnk=mkap_c&sublnk=2&screen=20 Jedoch gehört die Gleichsetzung von Schalldruck und Leistung an den Pranger: |
 |
 |
| Die Frequenzbewertung dBA und dBC wird bei der Messung von Geräuschen verwendet. Hierbei werden die Messgrößen durch ein bewertendes Filter gewichtet, das etwas den Frequenzgang des menschlichen Gehörs berücksichtigen soll. Um der Tatsache Rechnung zu tragen, dass das menschliche Ohr Töne mit gleichem Schalldruck in unterschiedlichen Tonhöhen verschieden laut empfindet, werden so genannte Frequenzbewertungskurven wie beispielsweise die durch Filter bewerteten Pegel dBA und dBC verwendet. |
| Ein weiteres schwieriges Thema ist: Wie nimmt denn die Lautstärke (Lautheit) mit der Entfernung von einer Schallquelle ab? Wie nimmt denn der Schalldruck (Spannung) mit der Entfernung von einer Schallquelle ab? Wie nimmt die Schallintensität (nicht die Schallleistung) mit der Entfernung von einer Schallquelle ab? Die Anfängerfrage dazu lautet ganz schlicht: Wie nimmt denn der Schall mit der Entfernung ab? |
Wenn bei einer Schalldruckpegelmessung der Abstand zur Schallquelle nicht angegeben |
Subjektiv empfundene Eigenschaften des Schalls
![]()
Addieren von gleich starken inkohärenten Schallsignalen
 |
|
||||||||||||||||||||||||||||||
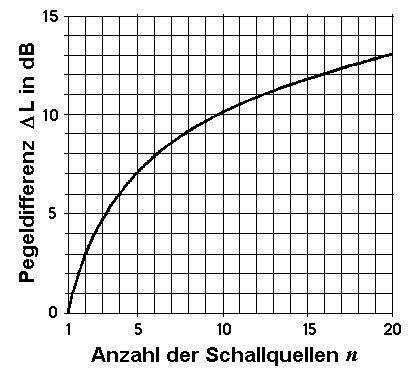
| Mehrere gleich starke Schallquellen erzeugen an einem bestimmten Ort einen Schalldruck, bzw. einen Schalldruckpegel. Bei der Addition solcher inkohärenter Quellen vereinfacht sich die Gleichung zur Berechnung des Summenschalldruckpegels wie folgt: |
Formeln: Δ L = 10·log n oder n = 10(ΔL/10)
Δ L = Pegelzunahme; n = Anzahl der gleichlauten Schallquellen.
| Für n = 2 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log 2 = +3,01 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 3 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log 3 = +4,77 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 4 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log 4 = +6,02 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. |
Pegelzunahme bei gleichstarken inkohärenten Schallquellen
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beiden Richtungen des ↔ Zeichens. |
| Der Gesamtpegel in dB ergibt sich aus dem Pegel einer Schallquelle, zu dem die Pegelzunahme (der Pegelzuwachs) in dB linear addiert wird. |
| Der ganz spezielle Sonderfall der aktiven Lärmkompensation durch auslöschende Pegeladdition - der mit "Antischall" bezeichnet wird - soll hier nicht betrachtet werden. |
Abnahme des Schalls mit der Entfernung
| Für eine Kugelwelle als Schallquelle gilt: Der Schalldruckpegel nimmt bei Verdopplung des Abstands um (−)6 dB ab. Der Schalldruck fällt also aufdas 1/2-fache (50 %) des Schalldruckanfangswerts. Der Schalldruck nimmt dabei im Verhältnis 1/r zum Abstand ab. Für eine Kugelwelle als Schallquelle gilt: Der Schallintensitätspegel nimmt bei Verdopplung des Abstands auch um (−)6 dB ab. Die Intensität fällt also auf das 1/4-fache (25 %) des Schallintensitätsanfangswerts. Die Schallintensität nimmt dabei im Verhältnis 1/r2 zum Abstand ab. Für eine Kugelwelle als Schallquelle gilt: Der Lautstärkepegel nimmt bei Verdopplung des Abstands auch um (−)6 dB ab. Die Lautstärke fällt daher auf das 2/3-fache (ca. 63 %) des empfundenen Lautheitsanfangswerts. Die Lautheit nimmt dabei im Verhältnis 1/(20,66r) = 1/(1,581 r) zum Abstand ab. Die Schallleistung nimmt bei Verdopplung des Abstands überhaupt nicht ab. Gedankenhilfe: Eine 100-Watt-Glühlampe hat in 1 m und in 10 m Entfernung wirklich immer die gleichen 100 Watt, die von der Lampe ständig abgestrahlt (emittiert) werden. Diese Watt ändern sich nicht mit der Entfernung. |
Schalldruck und Schallleistung − Wirkung und Ursache
| Die Verdopplung des "Lautstärkeeindrucks" soll eine Erhöhung des Schalldruckpegels um runde 10 dB erfordern. Wer weiß eigentlich genau, wie sich die Empfindung "klingt doppelt so laut" anhört? Eine Messung der Verdopplung des Schalldrucks entspricht dagegen genau +6 dB. |
Häufig vorkommende falsche Behauptungen mit Schallgrößen
im Zusammenhang mit dem Abstand von der Schallquelle.
Falsche Abnahme vom Schalldruck mit der Entfernung zur Schallquelle − ohne Quadrat! p ~ 1 / r
| Richtige Version | Falsche Formulierung |
| Der Schalldruck (Amplitude) nimmt bei zuneh- mender Entfernung von der Schallquelle mit 1/r ab. Das ist das reziproke Abstandsgesetz 1/r. |
Der Schalldruck (Amplitude) nimmt bei zuneh- mender Entfernung umgekehrt proportional mit dem Abstand-Quadrat, also mit 1/r2 ab. Sehr falsch |
| Der Schalldruckpegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/2 (50 %) des Schalldruck-Anfangswerts. |
Der Schalldruckpegel nimmt bei zunehmender Entfernung von der Schallquelle mit (−)3 dB je Abstandsverdopplung ab. falsch |
| Die Schallintensität (Energie) nimmt bei zunehmender Entfernung von der Quelle mit 1/r2 ab. Das ist das reziproke Quadratgesetz 1/r2. |
Die Schallintensität (Energie) nimmt bei zuneh- mender Entfernung von der Schallquelle umgekehrt proportional mit dem Abstand 1/r ab. falsch |
| Der Schallintensitätspegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/4 (25 %) des Intensitäts-Anfangswerts. |
Der Schallintensitätspegel nimmt bei zunehmender Entfernung von der Schallquelle mit (−)3 dB je Abstandsverdopplung ab. falsch |
Schalldruck ist nicht Schallintensität
| Weder die Schallleistung, noch der Schallleistungspegel nimmt bei Verdopplung
des Abstands um einen Wert bzw. um irgendwelche dBs ab. Weshalb ist das so? Der Schallleistungspegel quantifiziert die gesamte von einem Objekt als Schall abgestrahlte Energie. Anders als der Schalldruck ist die Schallleistung unabhängig von der Entfernung zum Objekt, dem umgebenden Raum und anderen Einflüssen. |
| Wie nimmt der Schall mit der Entfernung ab? Wie laut hören wir den Schall und wie misst man den Schall? |
| Knowing the intensity of a sound wave allows one to calculate the decibel (dB) level of that sound. Use the Decibel Calculator widget to determine the decibel rating from any intensity in Watt/meter2. Enter intensities using scientific notation - for example, enter 5e-5 for 5.0x10-5. |
| WolframAlpha Decibel Calculator |
| Determine the perceived loudness of a sound |
| Intensity and the Decibel Scale - The Physics Classroom |
| Faktor oder Verhältnis und Pegel in Dezibel (dB) |
| Halbe Lautstärke ≡ Pegel –10 dB | Doppelte Lautstärke ≡ Pegel +10 dB |
| Halber Schalldruck ≡ Pegel –6 dB | Doppelter Schalldruck ≡ Pegel +6 dB |
| Halbe Leistung ≡ Pegel –3 dB | Doppelte Leistung ≡ Pegel +3 dB |
| Vierfache Leistung ≡ Pegel +6 dB | Zehnfache Leistung ≡ Pegel +10 dB |
| Doppelter Abstand ≡ Pegel –6 dB | Doppelte Anzahl (Doppelte Leistung)+3 dB |
| Einfache Faustregel: Bei Arbeiten mit Leistung ist 3 dB das Doppelte und 10 dB das 10-fache. Beim Arbeiten mit Spannung oder Strom ist 6 dB das Doppelte und 20 dB das 10-fache. |
| zurück |
Suchmaschine |
Startseite |