Elektrische Spannung Physik Berechnung Leistung Spannung Strom Widerstand Leistungsformel Power Energie Arbeit Formel Formeln berechnen Physik Elektrizität Elektronik elektrische Formel Übersicht Maßeinheiten math pi Leistungsberechnung Stromspannung Stärke Stromstärke Formelsammlung Formel Leistung Physik Kenngrößen Physikunterricht Tontechnik - Sengpielaudio
 
English version UK-flag - sengpielaudio D-flag - sengpielaudio
 
Elektrischer Strom, elektrische Leistung
und elektrische Spannung
 
Elektrizität und elektrische Ladung
 
Die häufigsten allgemeinen Formeln in der Elektrotechnik
 
● Formeln und Berechnungen ●
 
Zusammenhang der physikalischen und elektrischen Größen (Kenngrößen)
 
Elektrische Spannung U, Stromstärke I, Widerstand R, Impedanz Z, Leistung P
Volt in V, Ampere in A, Widerstand und Impedanz in Ohm Ω und Watt in W
 
In der Physik sprechen wir von elektrischer Spannung und vom elektrischen Strom als Stromstärke.
Wie berechne ich die Stromspannung? Vermeide das komisch-falsche Wort Stromspannung,
das Reiseveranstalter und Rechtsanwälte gerne verwenden und ersetze es durch eines der folgenden
Worte: elektrische Spannung, Betriebsspannung oder Netzspannung. Selten sprechen Praktiker von
der Potentialdifferenz, wenn schlicht elektrische Spannung gemeint ist.
Auch wenn der Nachname des Namensgebers "Ampère" mit accent grave geschrieben wird, wird
die SI-Einheit im deutschen und englischen Sprachraum ohne Akzent, also "Ampere", geschrieben.
 
Für den Widerstand R wird oft die Nenn-Impedanz Z = 4, 8 und 16 Ohm angenommen (Lautsprecher)
Die Impedanz ist der Wechselstrom-Widerstand, der aus den Komponenten Kondensator, Spule und
ohmschem Widerstand gebildet wird und dessen Wert und Phasenlage sich mit der Frequenz ändert.
Das ohmsche Gesetz U = R · I oder das Ohm'sche Gesetz einschließlich der Leistung P = U · I; P = power.
I = international ampere, intensity oder lat. influare (hineinfließen), E = elektromotorische Kraft (EMK)
und R = resistance (widerstehen). U kommt von lat. urgere (drängen, treiben, drücken). U soll angeblich
auch "Unterschied" bedeuten, wegen der Potentialdifferenz als Unterschied oder auch als Spannungsabfall.
Wer das schnöde Wort Spannung nicht mag, der kann Spannung auch ganz vornehm (elektrische)
Potentialdifferenz nennen. Der Buchstabe I kann von "International Ampere", aber auch von lat. influare
(hineinfließen) kommen und R von resistance oder von resistare (widerstehen).
Formeln: URI und PUI.
 
Bitte zwei Werte eingeben - die anderen beiden Werte werden berechnet.

 
Spannung U   Volt V
Stromstärke I   Ampere A 
 Widerstand R   Ohm Ω
Leistung P   Watt W
 
 Für R nimm Impedanz Z 
 
Grundlagen der elektrischen Gesetze
Elektronik-Formelsammlung
 
 Das Formelrad  ▼   Wichtige Formeln  
      der Elektrotechnik         für die Elektronik
Elektrische Formeln in Kreis-Darstellung (Diagramm)
 
Formelrad Elektrotechnik
 
Das Formelrad der Elektrotechnik
 
Im Englischen ist U für Spannung nicht bekannt. Dort kennt man "voltage" = V oder E von "electro motive force"
Energie = Spannung · Ladung. E = U · Q. Für den Widerstand R ist auch die Impedanz Z zu nehmen.
 
Die 12 wichtigsten Formeln:
Spannung U = R · I = P / I = √(P · R) in Volt V            Stromstärke I = U / R = P / U = √(P / R) in Ampere A
Widerstand R = U / I = P / I2 = U2 / P in Ohm Ω       Leistung P = U · I = R · I2 = U2/ R in Watt W
 
Siehe auch: Das Formelrad der Akustik (Audio)

Regenbogenlinie

Red Power Dot Die großen Leistungsformeln   
         oder zeitgemäßer ausgedrückt "Die Mega Power-Formeln" 
        − Elektrische und mechanische Power-Berechnung (Stärke)  		 No real power formula

 Leistungsformel 1 – Elektrische Leistungsgleichung: Leistung P = U · I = R · I2 = U2 ⁄ R
 hierbei ist Leistung P in Watt, Spannung U in Volt und Stromstärke I in Ampere.
 Bei Wechselstrom muss zusätzlich der Leistungsfaktor cos φ, also der Leistungsfaktorwinkel φ
 (Phasenwinkel) zwischen Spannung und Strom beachtet werden.
 Elektrische Energie ist E = P · t − gemessen in Wattstunden oder auch in kWh. 1J = 1N·m = 1W·s
 
 Leistungsformel 2 – Mechanische Leistungsgleichung: Leistung P = Δ E / Δ t hierbei ist
 Δ W = verrichtete Arbeit entsprechend Δ E = aufgewendete Energie.
 Leistung P in Watt. Leistung P = Arbeit / Zeit (W ⁄ t).
 Energie E in Joule und Zeit t in Sekunden. 1 W = 1 Joule/Sekunde.
 Leistung = Kraft mal Weg (Auslenkung) durch Zeit, also P = F · s / t oder anders ausgedrückt:
 Leistung = Kraft mal Geschwindigkeit, also P = F · v.
 
 Der gesuchte druckvolle Sound ist nicht in diesen Formeln zu finden. Pass auf deine Ohren auf!
 Die Trommelfelle unserer Ohren und auch Mikrofone reagieren wirklich nur auf den Schalldruck
 und werden dadurch wirkungsvoll bewegt. Das bewirkt eben nicht die Intensität, die Leistung oder
 gar die Energie. Wer in der Tontechnik mit der gestaltenden Tonaufnahme befasst ist, der tut gut
 daran, sich weniger um die Ursache als Intensität, Leistung und Energie zu kümmern, sondern der
 achte eher auf die Wirkung von Schallwechseldruck p und Pegel (Schalldruckpegel) an den Ohren
 und den Mikrofonen, sowie der diesem allen entsprechenden Audiospannung U ~ p; siehe:
 Schalldruck und Schallleistung − Wirkung und Ursache
 Kräftig brüllende Lautsprecher − die gerne Boxen genannt werden − sollen recht viel "Power",
 also Leistung bringen; siehe hierzu besser den bedeutsamen Wirkungsgrad der Lautsprecher.
 Dazu gehört die typische Frage:
 Wieviel Dezibel sind eigentlich zweimal, dreimal oder viermal so laut?
 Einen Effektivwert (RMS) der Leistung als Energiegröße gibt es in Wirklichkeit nicht.
 Mit "RMS-Leistung" soll höchstens nicht ganz korrekt angedeutet werden, dass diese Leistung
 aus dem Produkt von Effektivspannung und Effektivstromstärke errechnet wurde. Lies doch mal:
 Warum es keine 'RMS Watt' oder 'Watt RMS' gibt - und auch niemals gab.
 "RMS" Power ist ein ziemlich dümmlicher Begriff, der jedoch unter Audio-Leuten beliebt ist.
 Leistung (Power) ist die Menge an Energie, die in einer bestimmten Zeiteinheit umgesetzt wird.
 Wer mehr Power haben will, der muss auch ständig mehr bezahlen.
Aha!
 
 
André-Marie Ampère war ein französischer Physiker und Mathematiker.
Die SI-Einheit der Messung des elektrischen Stroms in Ampere, wurde nach ihm benannt.
Alessandro Giuseppe Antonio Anastasio Volta war an italianischer Physiker.
Die SI-Einheit der Messung der elektrischen Spannung in Volt, wurde nach ihm benannt.
Georg Simon Ohm war ein deutscher Physiker und Mathematiker.
Die SI-Einheit der Messung des elektrischen Widerstands in Ohm, wurde nach ihm benannt.
James Watt war ein schottischer Erfinder und Maschinenbauer.
Die SI-Einheit der Messung der elektrischen Leistung in Watt, wurde nach ihm benannt.
 
 
 
In der analogen Tonstudiotechnik gibt es keine Leistungsanpassung.
In der Tontechnik (Audio) verwenden wir alleine Spannungsanpassung.
 
 
 
Leistung, ist wie alle Energiegrößen überwiegend eine berechnete Größe.
 
 
Aha!  
Das Wort "Leistungsverstärker" ist unzutreffend – besonders in der Tontechnik.
Spannung und Strom können verstärkt werden.
Der Begriff "Leistungs-Verstärker" ist eigenartig, aber man versteht darunter,
dass ein Verstärker eine Last antreiben soll - wie etwa einen Lautsprecher.
Wir nennen das Produkt aus Strom- und Spannungsverstärkung einfach
"Leistungsverstärkung".
 
 
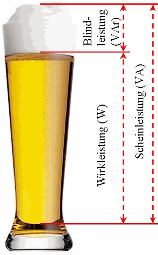Energie und Power        Bier - sengpielaudio

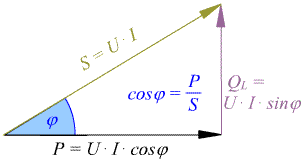Scheinleistung sengpielaudio

Scheinleistung =
√ (Wirkleitung2 +
Blindleistung2)
Courtesy of Brian Willis and Causeway Art Studio

Tipp: Das Dreieck der elektrischen Spannung U = R · I (Ohmsches Gesetz URI)

Bitte zwei Werte eingeben, der dritte Wert wird berechnet.

 
 Elektrische Spannung U  Volt Magisches Dreieck Ohm
Widerstand R  Ohm 
   Stromstärke I  Ampere 
U = R · I              I = U / R              R = U / I 

Tipp: Das Dreieck der elektrischen Leistung P = U · I (Leistungsgesetz PUI)

Bitte zwei Werte eingeben, der dritte Wert wird berechnet.

 
  Elektrische Leistung P  Watt Magisches Dreieck Leistung
Spannung U  Volt
Stromstärke I  Ampere   
P = U · I              I = P / U              U = P / I

Ein "Magisches Dreieck" kann verwendet werden, um alle Formeln recht einfach zu berechnen.
Der Wert, der berechnet werden soll, wird abgedeckt. Mit den beiden übrigen Werten wird das Ergebnis beerechnet.

Formel fuer Watt - sengpielaudio

Berechnungen: Ohmsches Gesetz - Das magische Dreieck

Blink-Linie

WECHSELSTROM (AC) ~

Ul = Netzspannung (Volt), Up = Phasen-Spannung (Volt), Il = Netzstromstärke (Ampere), Ip = Phasen-Stromstärke (Ampere)
Z = Impedanz (Ohm), P = Leistung (Watt) φ = Leistungsfaktor (Winkel), VAR = Volt-Ampere (reaktiv)

Stromstärke (Einzel-Phase): I = P / U · cos φ     Stomstärke (3 Phasen): I = P / √3 Ul · cos φ oder I = P / 3 U · cos φ 
Leistung (Einzel-Phase): P = Up · Ip · cos φ     Leistung (3 Phasen): P = √3 Ul · Il · cos φ oder P = √ 3 Up · Ip · cos φ 
Leistungsfaktor PF = cos φ = R/(R2 + X2)1/2, φ = Leistungsfaktorwinkel. Bei Gleichstrom ist PF = 1.

Der Term cos φ wird Leistungsfaktor, Wirkfaktor oder Verschiebungsfaktor genannt. Das ist
der Quotient aus Wirk- und Scheinleistung (cos φ = P/S) oder der Cosinus der Phasenverschiebung.
Die Scheinleistung S berechnet sich nach Pythagoras aus der Wirkleistung P und der Blindleistung Q.    S = √(P2 + Q2)

Formeln für Leistung bei Gleichstrom (DC power)
Spannungsberechnung U in (V) aus Stromstärke I in (A) und Widerstand R in (Ω):
U(V) = I(A) × R(Ω)
Die Leistungsberechnung P in (W) aus Spannung U in Volt (V) und Stromstärke I in (A):
P(W) = U(V) ×I(A) = U2(V) / R(Ω) = I2(A) × R(Ω)
 
Formeln für Leistung bei Wechselstrom (AC power)
Die Spannung U in Volt (V) ist gleich der Stromstärke I in Ampere (A) mal der Impedanz Z in Ohm (Ω):
U(V) = I(A) × Z(Ω) = (| I | × | Z |) und (θI + θZ)
Die Scheinleistung S in Volt-Ampere (VA) ist gleich der Spannung U in Volt (V) mal der Stromstärke I
in Ampere (A):
S(VA) = U(V) × I(A) = (| U | × | I |) und (θV − θI)
Die WirkleistungP in Watt (W) ist gleich der Spannung U in Volt (V) mal der Stromstärke I in Ampere
(A) mal dem Leistungsfaktor (cos φ):
P(W) = U(V) × I(A) × cos φ
Die Blindleistung Q in Volt-Ampere reaktiv (VAR) ist gleich der Spannung U in Volt (V) mal der
Stromstärke I in Ampere (A) mal dem Sinus des komlexen Leistungs-Phasenwinkels (φ):
Q(VAR) = V(V) × I(A) × sin φ
Der Leistungsfaktor (power factor FP) ist gleich dem Absolutwert vom Kosinus des komplexen
Leistungs-Phasenwinkels (φ):
PF = | cos φ |

Rainbow line

Elektrische Maßdefinitionen
Menge Name Definition
Frequenz f Hertz (Hz) 1/s
Kraft F Newton (N) kg·m/s²
Druck p Pascal (Pa) = N/m² kg/m·s²
Energie E Arbeit Joule (J) = N·m kg·m²/s²
Leistung P Watt (W) = J/s kg·m²/s³
Elektrische Ladung Q Coulomb (C) = A·s A·s
Spannung U Volt (V) = W/A kg·m²/A·s³
Strom I Ampere (A) = Q/s A
Kapazität C Farad (F) = C/V = A·s/V = s/Ω  A²·s4/kg·m²
Induktivität L Henry (H) = Wb/A = V·s/A kg·m²/A²·s²
Widerstand R Ohm (Ω) = V/A kg·m²A²·s³
Leitfähigkeit G Siemens (S) = A/V A²·s³/kg·m²
Magnetfluss Φ Weber (Wb) = V·s kg·m²/A·s²
Flussdichte B Tesla (T) = Wb/m² = V·s/m² kg/A·s²

Das Fließen von elektrischer Ladung Q wird als elektrischer Strom I bezeichnet. Die Ladungsmengenveränderung pro
Zeiteinheit ist die elektrische Stromstärke. Fließt ein Strom mit konstanter Stärke I während der Zeit t, so transportiert er
die Ladung Q = I · t. Für einen zeitlich konstanten Strom ist der Zusammenhang zwischen Ladung und Strom: I = Q / t
oder Q = I · t. Durch diese Beziehung der Basiseinheiten Ampere und Sekunde ist das Coulomb in Internationalen
Einheitensystem festgelegt. Die Einheit Coulomb lässt sich als 1 C = 1 A · s darstellen.
Ladung Q, (Einheit in Amperestunden Ah), Entladestrom I, (Einheit in Ampere A), Zeit t, (Einheit in Stunden h).

Die Akustische Äquivalenz zum Ohmschen Gesetz (Rechner)

In der Akustik gilt das akustische Äquivalent zum ohmschen Gesetz

Zusammenhang der akustischen Größen bei ebenen fortschreitenden Schallwellen

Umrechnungen von weiteren Einheiten, wie Leistung und Energie

Vorsilben | Länge | Fläche | Volumen | Gewicht | Druck | Temperatur | Zeit | Energie | Leistung | Dichte | Geschwindigkeit | Beschleunigung | Kraft

[Zum Seitenanfang]

 
 
zurück zurück Suchmaschine weiter Startseite start