

| English version |
 |
| Weil die Schallgeschwindigkeit c mit 0,6 m/s pro °C zunimmt, steigt dabei
auch die Tonhöhe der Blasinstrumente - also die Frequenz f - um etwa 3 cent (3/100 eines Halbtons). Die Wirkung der Materialausdehnung (Blech) auf Änderung der Tonhöhe ist dagegen recht bedeutungslos. |
Tonhöhenänderung J (Frequenz) in Abhängigkeit von der Umgebungstemperatur ϑ (theta)
bei schwingenden Luftsäulen, wie Flöten, Pfeifen und Rohren
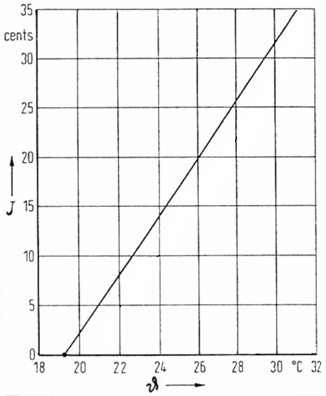 |
Aus: U. Pisani, "Effect of a Local Temperature Change in an Organ Pipe", Acustica, Vol.25 (1976), pp.133 ff.
| Man sollte sich klarmachen, wie bei einem Ton einer Orgelpfeife oder einem anderen Blasinstrument bei einer Temperaturerhöhung von beispielsweise 20°C nach 25°C, sich die Schallgeschwindigkeit c und somit auch das Produkt λ· f verändert. Da die Wellenlänge λ wegen der konstanten Länge der Orgelpfeife auch konstant bleiben muss, kann sich nur die Frequenz f, also die Tonhöhe ändern. |
| c = λ · f |
λ = c / f | f = c / λ | c ~ f |
|
Der Temperatureinfluss ist unabhängig von der Tonhöhe immer gleich. Das heißt, die ermittelte Abweichung in cent gilt für jeden Ton. Die Cent-Angabe ist also frequenzunabhängig. |
| Umrechnung von Frequenzverhältnis y in Intervallmaß J in cents: J = 1200 · (log y / log 2) Umrechnung von Intervallmaß J in cents in Frequenzverhältnis y: y = f2 / f1 = 10J·log (2/1200) |
| Mit folgender Formel ist die sich mit der Temperatur ändernde Schallgeschwindigkeit genauer zu berechnen. Schallgeschwindigkeit 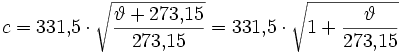 in m/s in m/sTemperatur ϑ in °C |
| Frequenzverhältnis (Frequenzveränderung) Änderung mit der Temperatur |
|
| Einfluss der Temperatur auf die Tonhöhe: Die Schallgeschwindigkeit in Luft − und damit die
Tonhöhe (Frequenz) einer Note als Luftsäule einer bestimmten Länge − ist direkt proportional der
Quadratwurzel aus der absoluten Temperatur. Die absolute Temperatur wird vom absoluten
Nullpunkt minus 273,15°C aus gemessen. Die Einheit ist 1 Kelvin (K) und hat die gleiche Größe
wie 1°C.
Beispiel: Die Frequenzveränderung y = f2 / f1 durch die Temperaturerhöhung von ϑ1 = 20°C auf ϑ2 = 24°C ist die Quadratwurzel aus [(273 + 24 = 297 K) / (273 + 20 = 293 K)] = 1,0069028 ... Deshalb erhöht sich eine Frequenz von 440 Hz bei 20°C auf (440 Hz · 1,0069028) = 443 Hz bei 24°C. Zu beachten ist, dass die Temperatur der Luft im Inneren des Blasinstruments recht komplex zwischen der Temperatur des Raums und dem Körper des Spielers liegt. Durch die Instrumentenerwärmung steigt die erzeugte Tonhöhe. |
| Ein geschultes Gehör nimmt etwa 5 cent Abweichung der Tonhöhe wahr; ein normales Gehör jedoch erst etwa 10 cent. Das bezieht sich auf nacheinander gespielte Töne. Erklingen in der Tonhöhe um 5 cent unterschiedliche Töne gleichzeitig, so ist die Schwebung schon recht auffällig wahrzunehmen. |
|
Tonhöhenänderung durch Änderung der Temperatur: Umrechnen der Frequenzen und Intervalle in Cent Temperaturabhängigkeit von physikalischen Größen Tonhöhenänderung von Orgelpfeifen bei Temperaturänderung Fragen zu "Tonhöhenänderung bei Temperaturänderung" Schalldruck und Schallleistung − Temperatur-Wirkung Tonhöhenänderung durch Änderung des Pegels: Tonhöhenänderung in Abhängigkeit vom Schallpegel 1 Tonhöhenänderung in Abhängigkeit vom Schallpegel 2 Effekt der Lautstärkeänderung auf die empfundene Tonhöhe S. S. Stevens, "The attributes of tones (1934) PNAS 1934 20 (7) 457 - 459" Bei tiefen Sinustönen scheint die Tonhöhe leicht höher zu werden, wenn die Lautstärke absinkt. Bei hohen Sinustönen scheint die Tonhöhe leicht höher zu werden, wenn die Lautstärke ansteigt. Dieser Effekt wird nur bei (reinen) Test-Sinustönen deutlich hörbar. Komplexe Töne zeigen keine Tonhöhenänderungen bei Pegeländerungen. Bei durchschlagenden Zungen (Akkordeon) ist die Schwingung unabhängig vom Medium (Luft, Wasser, sogar im Vakuum) und der Temperatur. Die Stimmzunge schwingt immer exakt gleich. |
Schallfrequenz in Wellenlänge und zurück
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Bei Dezimal-Eingabe ist der Punkt zu verwenden. |
Schallgeschwindigkeit und Temperatur in Luft
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Celsius in Fahrenheit und Fahrenheit in Celsius
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Für einem Grad Temperaturerhöhung steigt die Schallgeschwindigkeit
um 0,6 Meter pro Sekunde.
Prozentual gesehen ist das 0,6 / 343,5 =
0,00175 = 0,175%.
Ein Halbton ist eineVeränderung um 5,95% in der
Frequenz. Weil 0,175 / 5,95 = 0,03 ist, gibt es eine Tonhöhenänderung
von etwa 3 Cent für jede Temperaturänderung um 1 Grad bei
Blasinstrumenten. Ein "Cent" ist in diesem Zusammenhang ein Hundertstel Halbton, so wie ein Halbton ein Zwölftel einer Oktave ist. |
| Als absolutes Gehör oder Tonhöhengedächtnis bezeichnet man die meistens angeborene, aber auch erlernbare Fähigkeit eines Menschen, die Höhe eines beliebigen gehörten Tons zu bestimmen, d. h. ihn innerhalb eines Tonsystems exakt einzuordnen, ohne dabei einen Bezugston zu hören. Weitgehend ungeklärt ist, welche neuronalen Zusammenhänge für das absolute Gehör verantwortlich sind und welche Funktionen im Gehirn und dem Hörnerv dazu benötigt werden. |
Eine typische Frage: Wie ist die Beziehung zwischen Wellenlänge, Temperatur und Frequenz?
| zurück |
Suchmaschine |
Startseite |