

| English version |
| Dezibel sind logarithmische "Einheiten", die nicht wie andere Zahlen linear addiert werden dürfen. Erzeugt eine Quelle einen Pegel L1 und eine zweite Quelle, die aus der ersten stammt, einen kohärenten Pegel L2, (wie zwei dicht bei einander stehende Lautsprecher mit dem gleichen Signal), dann ergibt das einen Summen-Pegel der 6 dB höher ist als der Einzelpegel. Sind beide Pegel-Werte gleich, so ist das noch einfach. Anders sieht es aus, wenn beide kohärenten kombinierten Pegelwerte unterschiedlich sind. Mehr als 6 dB größer als der höhere der beiden kohärenten Pegel kann der Summenpegel aber niemals werden. Achtung: Diese Berechnung hier ist nicht zu verwechseln mit der üblichen akustischen Pegel-Addition zweier "inkohärenter" Quellen - wie z. B. einer Geige und einer Trompete. Siehe auch den anderen Fall: ● Pegeladdition von akustischen inkohärenten Schallquellen. |
Addition von Amplituden (und Pegeln)
 |
 |
|
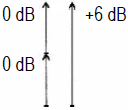
| Spannungssumme kohärent (0°) 1 + 1 = 2 |
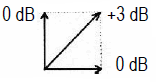
Leistungssumme inkohärent (90°) √ (1² + 1²) = 1,414... |
| Die Addition zweier kohärenter Druck- oder Spannungspegel ist: Die Addition zweier pegelgleicher Werte ergibt hier eine Anhebung des Gesamtpegels von (+)6 dB. Dieses erhält man bei gleicher Ansteuerung von zwei dicht nebeneinander stehenden Lautsprechern. Die Addition zweier inkohärenter Druck- oder Spannungspegel ist: Die Addition zweier pegelgleicher Werte ergibt eine Anhebung des Gesamtpegels von (+)3 dB. Diese Gleichung wird sowohl für die elektrische Addition inkohärenter Signale, als auch für die Berechnung des Energiepegels zweier Lautsprecher verwendet. |
Pegeladdition mehrerer kohärenter Signale
|
Das übliche Addieren der Pegel zweier inkohärenter Schallquellen Addition von Amplituden und Pegeln - kohärent und inkohärent Wie addieren sich Pegel beim Hören? Was ist eine Amplitude? |
![]()
Addieren von gleich starken kohärenten (!) Signalen
 |
|
||||||||||||||||||||||||||||||
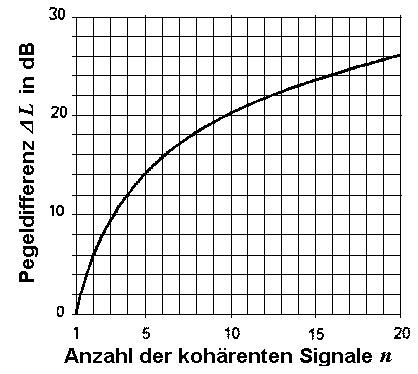
Formeln: Δ L = 20 × log n oder n = 10(ΔL/20)
Δ L = Pegelzunahme; n = Anzahl der gleich starken Quellen.
| Für n = 2 gleich starke, kohärente Quellen ergibt sich eine Pegelzunahme von 20 · log10 2 = +6,02 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 3 gleich starke, kohärente Quellen ergibt sich eine Pegelzunahme von 20 · log10 3 = +9,54 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 4 gleich starke, kohärente Quellen ergibt sich eine Pegelzunahme von 20 · log10 4 = +12,04 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 10 gleich starke, kohärente Quellen ergibt sich eine Pegelzunahme von 20 · log10 10 = +20,00 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. |
![]()
Pegelzunahme bei gleich starken kohärenten Signalen
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
|
Siehe auch: Addieren der Dezibel von benachbarten Terzbändernzum Pegel von einem Oktavband Addieren von bis zu 30 Pegeln in Dezibel |
| zurück |
Suchmaschine |
Startseite |