Total dB level adding of coherent correlated sound sources combining decibels or SPL sound pressure level audio logarithmic decibel scale loudspeaker add signal noise levels incoherent noncoherentt

● Total level adding of coherent signals ●
Fact: Voltage sum or Voltage addition

Adding the level of two steady correlated (in phase) sources
Coherent Signal Summing: This results from the fact that the sum voltage
will be twice the voltage of a single signal.

The used browser does not support JavaScript.
You will see the program but the function will not work.

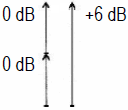
Decibels are logarithmic "units" that can not be added to other numbers linearly. If a source creates a level L₁ and a second source L₂ that is built from the first, (as two closely powered loudspeakers get the same signal), then this gives a sum of the level which is 6 dB higher than the level of one signal.
If both values are the same level, that's easy. The situation changes when both steady correlated or coherent combined levels are different. More than 6 dB higher than the higher of the two levels of the coherent sum level can never be reached.
Note: This calculation here should not be confused with the usual addition of two acoustic "incoherent" (noncoherent) sources - such as a violin and a trumpet. See also the other case:
● Total level adding of acoustical incoherent (noncoherent) sound sources.

Adding amplitudes (and levels)


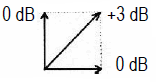
Voltage sum coherent (0°) 1 + 1 = 2		Power sum incoherent (90°) √ (1² + 1²) = 1,414...

Adding of two coherent pressure or voltage level:

Adding of two values of the same level results in an increase in the overall level here of (+) 6 dB.
This is obtained with the equal input of two closely standing speakers.

Adding of two incoherent (noncoherent) pressure or voltage level:

Adding of two values of the same level results in an increase of the total level of (+) 3 dB.
This equation is used for both the electric incoherent addition of signals, and for the calculation
of the energy level of two loudspeakers.

Level addition of several coherent signals

Total level adding of incoherent sources
Amplitude sum and squared total amplitude in dB
How do Sound Pressure Levels add when listening?
What is amplitude?

Adding of equal strong coherent signals

Level increase Δ L for n equal coherent signals
Number of n equal loud sound sources	Level increase Δ L in dB
1	0
2	6.0
3	9.6
4	12.0
5	14.0
6	15.6
7	17.0
8	18.0
9	19.0
10	20.0
12	21.6
16	24.0
20	26.0

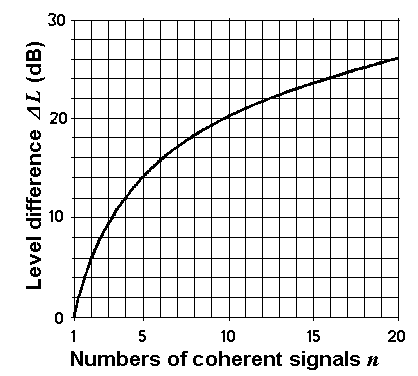
Formulas: Δ L = 20 × log n or n = 10^(ΔL/20)
Δ L = level difference; n = number of equal coherent sources.

n = 2 coherent sources of equal level result in a higher level of
20 × log₁₀ 2 = +6.02 dB compared to the case that only one source is available.
n = 3 coherent sources of equal level result in a higher level of
20 × log₁₀ 3 = +9.54 dB compared to the case that only one source is available.
n = 4 coherent sources of equal level result in a higher level of
20 × log₁₀ 4 = +12.04 dB compared to the case that only one source is available.
n = 10 coherent sources of equal level result in a higher level of
20 × log₁₀ 10 = +20.00 dB compared to the case that only one source is available.

Adding (combining) equal strong coherent sources

Simply enter the value to the left or the right side.
The calculator works in both directions of the ↔ sign.

The total level in dB is the level of one source plus the increase of level in dB.

back

Search Engine

home

Adding equal strong coherent sources
Number of sound sources n	↔	Increase of level Δ L dB