Intervall Umrechnung: Frequenzverhaeltnis nach cent und cents nach Hertz Hz (Herz) Frequenz Verhaeltnis Ratio umrechnen Audio Halbton Ganzton Toene

● Umrechnung der Intervalle − ¢ = cent ●

• Frequenzverhältnis nach cent und cent nach Frequenz ( Ratio) •

Tonhöhenänderung durch Temperaturänderung

1 Hertz = 1 Hz = Schwingungen pro Sekunde
Die Einheit die am häufigsten verwendet wird um Intervalle zu messen
wird cent genannt, von Lateinisch centum, das bedeutet "hundert".
Die Einheit steht für ein Hundertstel des gleichtemperierten Halbtons.
Mit anderen Worten, eine Oktave besteht aus 1200 Cent.

Der verwendete Browser unterstützt leider kein JavaScript. Das Programm
wird zwar angezeigt, aber die eigentliche Funktion ist nicht vorhanden.

Fülle die entsprechenden grauen Eingabe-Felder aus und klicke auf "Berechnung".

Es gibt keine Umrechnung von Hz in cents und zurück.
Bis nach unten runterscrollen: "Tabelle der Cent-Unterschiede".
Begründung: Cent ist eine logarithmische Maßeinheit eines Intervalls, stellt also ein dimensionsloses "Frequenzverhältnis" f₂ / f₁ dar.

Berechnung: Intervalle (cents) und Frequenz (Hz) als Excel-Programm (xlsx)

Unterschiedliche Terzen
Terzen

Cent-Wert-Ermittlung eines Intervalls

Anstelle der Frequenzen in Hz kann man auch die Zahlen 4 und 5 − z. B. bei den Bruchzahlen 4/5 des Intervalls nehmen.

Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Formel zum Intervall-Umrechnen: Frequenzverhältnis f₂ / f₁ nach cents (c).

¢ oder c = 1200 · log₂ (f₂ / f₁)
log 2 = 0,301029995

Die Formel enthält log₂ (Logarithmus zur Basis 2). Diese Formel kann auch mit der
Funktion log₁₀ ausgedrückt werden, welche die meisten Taschenrechner kennen:

c = 1200 · 3,322038403 log₁₀ (f₂ / f₁)
1/log 2 = 1/0,301029995 = 3,322038403

Die Formel mit log₁₀ ausgedrückt anstatt log 2.

3,322038403 ist der Umrechnungsfaktor, der den Logarithmus zur Basis 2 in den
Logarithmus zur Basis 10 umrechnet.
1 Cent = 2^(1/1200) = 1.0005777895065548592967925757932
Ein cent ist somit die Zahl, die 1200 Mal mit sich selbst multipliziert die Zahl 2 ergibt.
Der Centwert eines Intervalls wird aus dem Intervallfrequenzverhältnis wie folgt berechnet: (ln vom Intervallfrequenzverhältnis / ln 2)×1200 = Centwert des Intervalls.
Ein Halbton-Interval entspricht: 2(1/12) = 1,0594630943592952645618252949463. Somit ist: [ln (2(1/12)) / ln (2)]×1200 cent = 100 cent.

Das Pytagoreische Komma ist das Frequenzverhältnis (3/2)¹² / 2⁷ =
3¹² / 2¹⁹ = 531441 / 524288 = 1,0136432647705078125.
Das ergibt umgerechnet 23,460010384649013 cent.
Zwölf reine Quinten (3/2) ergeben 8423,46 Cent und
sieben Oktaven ergeben dagegen nur 8400 Cent.

Umrechnung von Halbtonschritten
Ein Intervall ist der Unterschied zwischen zwei Tonhöhen oder
der Abstand zwischen zwei Frequenzen in Bezug auf Halbtöne.

Gib zwei bekannte Werte ein und drücke "Berechnen".
Der dritte Wert wird berechnet. Bitte nur zwei Werte eingeben.
Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Frequenz-Berechnung bei unterschiedlichen
Oktav-Einteilungen

Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Tonhöhenänderung durch Temperaturänderung

Änderung einer Frequenz um einen Cent-Wert

Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Frequenz in Notennamen (Töne) umrechnen

Wie heißt die Note einer gegebenen Frequenz? Englische Bezeichnung.

Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Formeln: f = 440 · 2^(−58/12) · (2^(1/12))ⁿ und f = 440 · 2^{((n−58)/12)}

Die Originalprogrammquelle von Iain W. Bird ist weiterhin fehlerhaft:
http://www.birdsoft.demon.co.uk/music/notecalc.htm

Die Frequenz von 440 Hz ist der Kammerton 'a' oder A4 in englischer Bezeichnung.
Wenn jemand etwas anderes behauptet, dann irrt dieser. Siehe auch:

Tabelle: Frequenzen der gleichstufigen Stimmung und Notennamen

Tonhöhenänderung durch Temperaturänderung

Die Frequenz im Halbtonabstand von a' = 440 Hz

Für einen Ton der n Halbtöne höher (oder −n Halbtönen tiefer) als der Kammerton 440 Hz liegt, ist die Frequenz f_n = 2^n/12 · 440 Hz.
Umgekehrt kann man die Anzahl der Halbtöne im Abstand n vom Kammerton 440 Hz bestimmen: n = 12 · log₂(f_n / 440 Hz).

Einfach den Wert links oder rechts eingeben.
Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Masterclock-Rechner (Taktfrequenz)

Einfach den Wert links oder rechts eingeben.
Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

Rechner mit Eingabe der Referenz-Frequenz

Bei Dezimal-Eingabe ist stets der Punkt zu verwenden.

100 cent entsprechen einem Halbton.
Für Abwärtsstimmung kann Referenz-Frequenz und Flügelstimmung getauscht werden.

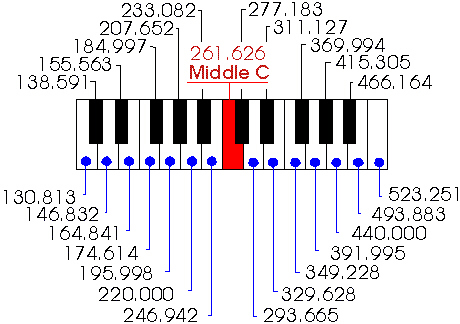
Klaviatur, Frequenzen, Notennamen und Piano-Tastatur

Berechnen der Harmonischen aus der Grundfrequenz

Tonhöhenänderung durch Temperaturänderung

Oktav-Einteilung: 12-tönige gleichschwebend temperierte Stimmung
(gleichstufig gestimmt oder gleichmäßig temperiert)

Intervall	Frequenzverhältnis	cent
Unisono	1,000000 : 1	0
Halbton oder kleine Sekunde	1,059463 : 1	100
Ganzton oder große Sekunde	1,122462 : 1	200
Kleine Terz	1,189207 : 1	300
Große Terz	1,259921 : 1	400
Reine Quarte	1,334840 : 1	500
Überm. Quarte / Verm. Quinte	1,414214 : 1	600
Reine Quinte	1,498307 : 1	700
Kleine Sexte	1,587401 : 1	800
Große Sexte	1,681793 : 1	900
Kleine Septime	1,781797 : 1	1000
Große Septime	1,887749 : 1	1100
Oktave	2,000000 : 1	1200

In der folgenden Tabelle sind für die bekanntesten reinen Zweiklänge bis zur Oktave ist das Frequenzverhältnis als Maß für die Konsonanz sowie die Klangempfindung der meisten Menschen aufgeführt:

Zweiklang	Frequenz- verhältnis	Konsonanz- wert	Klangempfindung
kleine Sekunde	16:15	15,49	sehr dissonant
große Sekunde	9:8	8,49	dissonant
kleine Terz	6:5	5,48	konsonant ("Moll")
große Terz	5:4	4,47	konsonant ("Dur")
Quarte	4:3	3,46	konsonant
Tritonus	45:32	37,95	sehr dissonant
Quinte	3:2	2,45	sehr konsonant ("neutral")
kleine Sexte	8:5	6,32	konsonant ("Moll")
große Sexte	5:3	3,87	konsonant ("Dur")
kleine Septime	16:9	12,00	dissonant
große Septime	15:8	10,95	dissonant
Oktave	2:1	1,41	sehr konsonant ("neutral")

Intervall-Name	Frequenzverhältnis	In cent (gerundet)	Gleichstufige Stimmung (cent)
Prime	1:1	0	0
Kleine Sekunde (Halbton)	16:15	112	100
Große Sekunde	10:9 (Kleiner Ganzton) 9:8 (Großer Ganzton)	182 204	200
Kleine Terz	6:5	316	300
Große Terz	5:4	386	400
Quarte	4:3	498	500
Übermäßige Quarte oder verminderte Quinte oder Tritonus	Hier gibt es verschiedene Definitionen: 7/5 (Huygens' Tritonus) 45:32 (diatonischer Tritonus) √2 : 1 (gleichstufige Stimmung) 10:7 (Eulers Tritonus)	582 590 600 617	600
Quinte	3:2	702	700
Kleine Sexte	8:5	814	800
Große Sexte	5:3	884	900
Kleine Septime	16:9	996	1000
Große Septime	15:8	1088	1100
Oktave	2:1	1200	1200

Name des Intervalls	Zusammensetzung der Intervalle	Schwingungs- verhältnis	Intervall- Abstand in cent	Gleichst. temp. in cent
Syntonisches Komma	gGT - kGT	81 : 80	21,51	0
Pythagoräisches Komma	12 Quinten - 7 Okt	531441 : 524288	23,46	0
Kleines Chroma	kGT - HT	25 : 24	70,67	100
Limma	3 Okt - 5 Quinten	256 : 243	90,22	100
Großes Chroma	gGT - HT	135 : 128	92,18	100
Halbton, kleine Sekunde	HT	16 : 15	111,73	100
Apotome	7 Quinten - 4 Okt	2187 : 2048	113,69	100
Kleiner Ganzton, gr.Sekunde	kGT	10 : 9	182,40	200
Großer Ganzton, gr. Sekunde	gGT	9 : 8	203,91	200
Pythagoras, kleine Terz	kGT + HT	32 : 27	294,13	300
Kleine Terz	gGT + HT	6 : 5	315,64	300
Große Terz	gGT + kGT	5 : 4	386,31	400
Pythagoras, große Terz	gGT + gGT	81 : 64	407,82	400
Reine Quarte	gGT + kGT + HT	4 : 3	498,04	500
Weite Quarte	gGT + gGT + HT	27 : 20	519,55	500
Verminderte Quinte	Okt - gGT - gGT - gGT	1024 : 729	588,27	600
Tritonus	gGT + kGT + gGT	45 : 32	590,22	600
Übermäßige Quarte	gGT + gGT + gGT	729 : 512	611,73	600
Enge Quinte	Okt - gGT - gGT - HT	40 : 27	680,45	700
Reine Quinte	Okt - gGT - kGT - HT	3 : 2	701,96	700
Pythagoras, kleine Sexte	Okt - gGT - gGT	128 : 81	792,18	800
Kleine Sexte	Okt - gGT - kGT	8 : 5	813,69	800
Große Sexte	Okt - gGT - HT	5 : 3	884,36	900
Pythagoras, große Sexte	Okt - kGT - HT	27 : 16	905,87	900
Enge kleine Septime	Okt - gGT	16 : 9	996,09	1000
Weite kleine Septime	Okt - kGT	9 : 5	1017,60	1000
Große Septime	Okt - HT	15 : 8	1088,27	1100
Große "Leit"-Septime	Okt - Limma	243 : 128	1109,78	1100
Oktave	Okt	2 : 1	1200,00	1200

Interval	Genauer temperierter Wert	Dezimal Wert	Reines Interval	Prozentualer Unterschied
Prime	1	1,000000	1 = 1,000000	0,00%
Kleine Sekunde		1,059463	16/15 = 1,066667	−0,68%
Große Sekunde		1,122462	9/8 = 1,1250000	−0,23%
Kleine Terz		1,189207	6/5 = 1,200000	−0,91%
Große Terz		1,259921	5/4 = 1,250000	+0,79%
Reine Quarte		1,334840	4/3 = 1.333333	+0,11%
Verminderte Quinte		1,414214	7/5 = 1,400000	+1,02%
Reine Quinte		1,498307	3/2 = 1,500000	−0,11%
Kleine Sexte		1,587401	8/5 = 1,600000	−0,79%
Große Sexte		1,681793	5/3 = 1,666667	+0,90%
Kleine Septime		1,781797	16/9 = 1,777778	+0,23%
Große Septime		1,887749	15/8 = 1,875000	+0,68%
Oktave		2,000000	16/8 = 2,000000	0,00%

Die Centzahl ist ein relatives Verhältnismaß für die Frequenzen von Schwingungen.
Ordnungsrahmen ist die Oktave, die einer Verdoppelung der Frequenz entspricht.
Diese lässt sich geometrisch mit einem konstanten Faktor (nicht arithmetisch!) in
beliebiger Weise unterteilen. Z. B. 220 bis 440 Hz.:
220 × ¹²√2 × ¹²√2 usw. = 440. Diese Teilung entspräche den Halbtonschritten der wohltemperierten äquidistanten
Stimmung. Der Name cent resultiert aus der Definition eines Halbtonschritts mit
100 cents. Daher: 220 ×¹²⁰⁰√2 × ¹²⁰⁰√2 = 440 weil: [¹²⁰⁰√2]¹²⁰⁰ = 2 ist. Nach diesem Muster sind beliebige Teilungen möglich,
z. B. eine äquidistant heptatonische mit ⁷√2 als Teilung. Die Centzahl selbst wird definiert durch: cent = 1200 × log(f₁/f₂) / log 2 und log 2 = 0,301029995
Sind die cent gegeben und ist das Frequenzverhältnis gefragt, so gilt:
x = 2^cents/1200.

Ein temperierter Halbton (1/2-Ton) hat das Frequenzverhältnis von ¹²√2 = 2^1/12 = 1,0594630943592952645618252949463
Ein temperierter Viertelton (1/4-Ton) hat das Frequenzverhältnis von ²⁴√2 = 2^1/24 = 1,0293022366434920287823718007739
Ein temperierter Achtelton (1/8-Ton) hat das Frequenzverhältnis von ⁴⁸√2 = 2^1/48= 1,0145453349375236414538678576629

Frage: Wie kann man cents in Hz umrechnen?
Antwort: Man kann nicht cents in Hertz umrechnen, weil cents keine Frequenz sind.
Cents sind eine Messung zwischen Intervallen, also einem "Frequenzverhältnis" f₂/f₁.

Hier ist eine Tabelle der Cent-Unterschiede für einige Frequenzen dicht bei 440 Hz:

Frequenz	Abweichung
435 Hz	−19,78 cent
436 Hz	−15,81 cent
437 Hz	−11,84 cent
438 Hz	−7,89 cent
439 Hz	−3,94 cent
440 Hz	±0 cent
441 Hz	+3,93 cent
442 Hz	+7,85 cent
443 Hz	+11,76 cent
444 Hz	+15,67 cent
445 Hz	+19,56 cent

Somit ist der Umrechnungsfaktor 4 cents / Hz für Stimmzwecke ausnahmsweise gültig nur dicht in der Nähe von 440 Hz.
Es gibt keine Umrechnung von Hz in cents und zurück.
Begründung: Cent ist eine logarithmische Maßeinheit eines Intervalls, stellt also ein dimensionloses "Frequenzverhältnis" f₂ / f₁ dar.

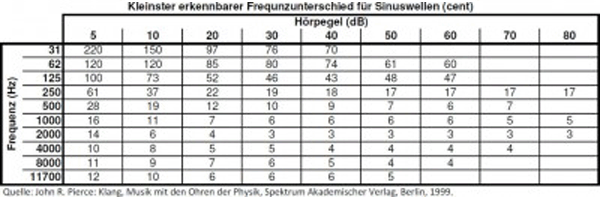
Kleinster erkennbarer Frequenzunterschied für Sinustöne bei unterschiedlichen Hörpegeln

Kleinster erkennbarer Unterschied fuer Sinustoene

zurück

Suchmaschine

Startseite


Halbtöne n im Abstand von a' Halbtöne	↔	Frequenz f_n - Bezug: 440 Hz Hz

n = 12(log (f_n/440) / log(2)) f_n = 2^(n/12)440


Referenz-Wordclock 48.0 kHz Piano-Stimmung f Hz	↔	Referenz-Frequenz 440 Hz Studio-Wordclock f_s kHz


Referenz-Wordclock 44.1 kHz Piano-Stimmung f Hz	↔	Referenz-Frequenz 440 Hz Studio-Wordclock f_s kHz