

| English version |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
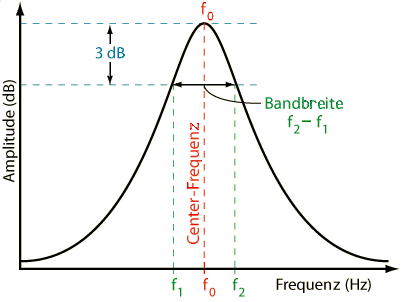 |
B = Δf = f0 / Q Q = f0 / B f0= B · Q = √ (f1 · f2)
B = f2 − f1 f1 = f02 / f2 = f2 − B
f2 = f02 / f1 = f1 + B
Formel zur Umwandlung von 'Bandbreite in Oktaven' N in Gütefaktor Q:
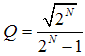 |
Formel zur Umwandlung von Gütefaktor Q in 'Bandbreite in Oktaven' N:
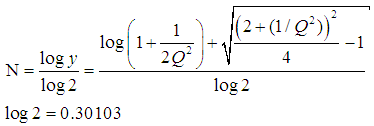 |
Auch ist diese längere Formel mit 4 Q bekannt; siehe seine Entwicklung:
Bandwidth in octaves versus Q in bandpass filters - RANE
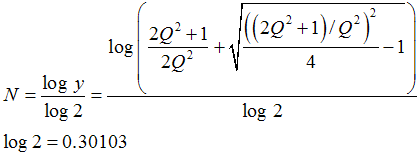 |
Frequenzverhältnis einer Oktave:
 |
Formel zur Umwandlung von Gütefaktor Q in 'Bandbreite in Oktaven' N,
jedoch mit dem logarithmus naturalis :
 |
Und die superkurze Formel zur Umwandlung von Gütefaktor Q in
'Bandbreite in Oktaven' N, jedoch mit sinh−1 , wenn man das auf seinem Rechner hat :
 |
Die Umrechnung der Bandbreite in Abhängigkeit von einem anderen Intervall als der Oktave, wie z. B. die
Angabe der "Bandbreite in Abhängigkeit einer Quinte" mit dem Intervall 2/3 oder 1/2 Oktave ist unüblich.
| Gegeben −3 dB-Punkte, um Bandbreite B und Gütefaktor Q zu finden. B = f0 / Q Q = f0 / B f0 = √ (f1 × f2) Gegeben Bandbreite in Oktaven N um den Gütefaktor Q zu finden. Q = sqr(2^N) / (2^N − 1) Gegeben Gütefaktor Q, um Bandbreite in Oktaven N zu finden. N = log(1 + 1 / (2 × Q2) + sqr(((2 + 1 / (Q2))2) / 4 − 1)) / log(2) |
Umrechnungstabelle
'Bandbreite in Oktaven' N in Gütefaktor Q
| N = B in Oktaven |
Güte- faktor Q |
N = B in Oktaven |
Güte- faktor Q |
N = B in |
Güte- faktor Q |
N = B in |
Güte- faktor Q |
|||
| 1/80 | 115,4 | 1 | 1,41 | 4 | 0,267 | 7 | 0,089 | |||
| 1/60 | 86,6 | 1 1/4 | 1,12 | 4 1/4 | 0,242 | 7 1/4 | 0,082 | |||
| 1/50 | 72,1 | 1 1/3 | 1,04 | 4 1/3 | 0,234 | 7 1/3 | 0,079 | |||
| 1/40 | 57,7 | 1 1/2 | 0,92 | 4 1/2 | 0,220 | 7 1/2 | 0,075 | |||
| 1/30 | 43,3 | 1 2/3 | 0,82 | 4 2/3 | 0,207 | 7 2/3 | 0,071 | |||
| 1/25 | 36,1 | 1 3/4 | 0,78 | 4 3/4 | 0,200 | 7 3/4 | 0,068 | |||
| 1/20 | 28,9 | 2 | 0,67 | 5 | 0,182 | 8 | 0,063 | |||
| 1/16 | 23,1 | 2 1/4 | 0,58 | 5 1/4 | 0,166 | 8 1/4 | 0,058 | |||
| 1/12 | 17,3 | 2 1/3 | 0,56 | 5 1/3 | 0,161 | 8 1/3 | 0,056 | |||
| 1/10 | 14,4 | 2 1/2 | 0,51 | 5 1/2 | 0,152 | 8 1/2 | 0,053 | |||
| 1/8 | 11,5 | 2 2/3 | 0,47 | 5 2/3 | 0,143 | 8 2/3 | 0,050 | |||
| 1/6 | 8,65 | 2 3/4 | 0,45 | 5 3/4 | 0,139 | 8 3/4 | 0,048 | |||
| 1/5 | 7,20 | 3 | 0,40 | 6 | 0,127 | 9 | 0,044 | |||
| 1/4 | 5,76 | 3 1/4 | 0,36 | 6 1/4 | 0,116 | 9 1/4 | 0,041 | |||
| 1/3 | 4,32 | 3 1/3 | 0,35 | 6 1/3 | 0,113 | 9 1/3 | 0,039 | |||
| 1/2 | 2,87 | 3 1/2 | 0,33 | 6 1/2 | 0,106 | 9 1/2 | 0,037 | |||
| 2/3 | 2,14 | 3 2/3 | 0,30 | 6 2/3 | 0,100 | 9 2/3 | 0,035 | |||
| 3/4 | 1,90 | 3 3/4 | 0,29 | 6 3/4 | 0,097 | 9 3/4 | 0,034 | |||
| 10 | 0,031 |
Q-Faktor in Abhängigkeit von der Bandbreite in Oktaven N
| Bandbreite in Oktaven N |
Filter Q-Faktor |
| 3,0 groß | 0,404 gering |
| 2,0 | 0,667 |
| 1,5 | 0,920 |
| 1,0 | 1,414 |
| 2/3 | 2,145 |
| 1/2 | 2,871 |
| 1/3 | 4,318 |
| 1/6 | 8,651 |
| 1/12 klein | 17,310 hoch |
|
Merke: Hoher Gütefaktor = kleine (schmale) Bandbreite bzw. geringer Gütefaktor = große (breite) Bandbreite. |
| Eine hohe Filtergüte bedeutet schmalbandige Filterung (Notch) bei großem Q-Faktor. Das sind steile Filterflanken bei kleiner Bandbreite. Eine geringe Filtergüte bedeutet breitbandige Filterung bei kleinem Q-Faktor. Das sind flache Filterflanken bei großer Bandbreite. Je größer das Q - umso enger ist die Resonanzspitze. Je kleiner das Q - umso breiter ist die Resonanzspitze. |
Notch-Filter haben einen großen Gütefaktor (Q-Faktor), entsprechend einer kleinen Bandbreite.
| Der Gütefaktor oder die Bandbreite ist nicht die "Flankensteilheit" in dB/Okt. |
| Slope in dB/oct = Steilheit der Filter-Flanken = Flankensteilheit ● Nur bei Hoch- und Tiefpassfiltern − nicht bei Glockenkurven ● |
| Merke: Der Gütefaktor oder die Bandbreite ist nicht in die "Flankensteilheit" als dB/Okt. umzurechnen. Es gibt Mastering-Equalizer mit unrichtiger Angabe der Filtereinstellung als "Slope in dB/octave" und nicht Q-Faktor (Width); siehe hierzu: Flankensteilheit (Slope in dB/Oct) ist nicht Bandbreite. |
| Mit "Güte" ist nicht gemeint, wie wertvoll das Signal ist. Es ist die Güte des Filters gemeint. Bei einem Filter mit flachen Flanken werden viele Frequenzen um die Einsatzfrequenz herum beeinflusst. Das Filter hat also eine größere Bandbreite, der so genannte Gütefaktor wird dabei mit einer niedrigen Zahl angegeben. Besitzt das Filter steile Flanken, ist dessen Bandbreite geringer. Hierbei werden wenige Frequenzen unterhalb und oberhalb seiner Einsatzfrequenz beeinflusst und der Gütefaktor Q wird dabei mit einer hohen Zahl angegeben. |
| Warum wird die Bandbreite und die Grenzfrequenz mit dem Pegel "−3 dB" angegeben? Warum nehmen wir immer 3 dB nach unten beim Pegel eines Filters? Halbwertsbreite = Full width at half maximum - FWHM. Das ist der Punkt, an dem die Energie (Leistung) auf den Wert ½ gesunken ist oder auf 0,5 = 50 Prozent der ursprünglichen Leistung als Energiegröße, entsprechend (−)3 dB = 10·log(0,5). Ein (−)3 dB Leistungsabfall ist ein Abfall um 50% auf 50%. Die Spannung ist dabei auf den Wert √(½) gesunken oder auf 0,7071 = 70,71 Prozent der ursprünglichen Spannung als Feldgröße, entsprechend (−)3 dB = 20·log(0,7071). Ein (−)3 dB Spannungsabfall ist ein Abfall um 29,29% auf 70,71%. |
| (−)3 dB bedeutet ½ (die Hälfte) der Leistung. Da die elektrische Leistung proportional zum Quadrat der Spannung ist, ergibt sich ein Wert von 0,7071 oder 70,71% der Durchlass-Spannung. √½ = 1/√2 = √0,5 = 0,7071. P ~ U2, also 0,5 ~ 0,70712. |
| Tontechniker und Sound-Designer ("Ohrenmenschen") verwenden gern die (Schall-)Feldgröße, darum heißt es: Die Grenzfrequenz eines Geräts (Mikrofon, Verstärker, Lautsprecher) ist diejenige Frequenz, bei welcher der Ausgangsspannungspegel auf einen Wert von (−)3 dB unter den Eingangsspannungspegel (0dB) gesunken ist. ● (−)3 dB entspricht dem Faktor √½ = 1/√2 = 0,7071. Das ist 70,71% der Eingangsspannung. Akustiker und Schallschützer ("Lärmbekämpfer") drücken dieses mit der (Schall-)Energiegröße etwas anders aus: Die Grenzfrequenz eines Geräts (Mikrofon, Verstärker, Lautsprecher) ist diejenige Frequenz, bei welcher der Ausgangsleistungspegel auf einen Wert von (−)3 dB unter den Eingangsleistungspegel (0 dB) gesunken ist. ● (−)3 dB entspricht dem Faktor ½ = 0,5. Das ist 50% der Eingangsleistung (die Hälfte). |
| Merke: Power gain - also Leistungsverstärkung - ist in der Audiotechnik (Tontechnik) nicht üblich. Selbst Leistungsverstärker für Lautsprecher verstärken keine Leistung. Sie verstärken die Audio-Spannung, welche die Schwingspule bewegt. |
| Schallfeldgröße
Schalldruck, Schallschnelle, Amplitude, Schallauslenkung, Spannung, (Stromstärke, elektrischer Widerstand). Reziprokes Abstandsgesetz 1/r |
Schallenergiegröße Schallintensität, Schallenergiedichte, Schallenergie, Schallleistung, (elektrische Leistung). Reziprokes Quadratgesetz 1/r² |
| Merke: Schallfeldgröße (Schalldruck p, elektrische Spannung U) ist nicht Schallenergiegröße
(Schallintensität I, Schallleistung Pak). I ~ p2 bzw. P ~ U2. Bisweilen hört man auch die Aussage: Die Grenzfrequenz liegt dort, wo der Pegel L, um (−)3 dB gesunken ist. Was immer der Anwender uns damit genauer mitteilen will: Pegel ist Pegel oder dB ist dB. |
| zurück |
Suchmaschine |
Startseite |