

| English version |
| Das geometrische Mittel zwischen zwei Zahlenwerten (Formel): Das arithmetische Mittel zwischen zwei Zahlwerten ist: Als Beispiel sind hier die Grenzfrequenzen einer Telefonübertragung angegeben: f1 = 300 Hz und f2 = 3300 Hz, wobei die richtige Mittenfrequenz f0 = 995 Hz das geometrische Mittel ist und nicht die 1800 Hz der Berechnung des arithmetischen Mittels. Was für ein großer Unterschied! |

| Telefonübertragungsbereich in logarithmischer Einteilung. Die Mittenfrequenz ist 995 Hz. Der Abstand von 300 Hz bis 995 Hz ist gleich dem lin. Abstand von 995 Hz bis 3300 kHz. Der Frequenzbereich 300 Hz bis 3,3 kHz ist die Bandbreite der Übertragung von 3 kHz. Manchmal geht der Telefonbereich sogar bis 3,4 kHz. |
![]()
| Der Hi-Fi-Hörbereich ist von f1 = 20 Hz und f2 = 20000 Hz angegeben, wobei die richtige Mittenfrequenz f0 = 632,5 Hz (!) das geometrische Mittel ist und nicht die 10,01 kHz aus der Berechnung des arithmetischen Mittels. Dieses ist häufig nicht klar! |

| Hörbereich in logarithmischer Einteilung. Der lin. Abstand von 20 Hz bis 632 Hz ist gleich dem Abstand von 632 Hz bis 20 kHz. Siehe die angegebenen Punkte. |
Durch die Definition der Mittenfrequenz sind die Verhältnisse der Grenzfrequenzen zur
Mittenfrequenz gleich: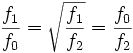 Das geometrische Mittel zweier Zahlen ist die Quadratwurzel ihres Produkts. Das geometrische Mittel dreier Zahlen ist die dritte Wurzel ihres Produkts. Das arithmetische Mittel ist die Summe der Zahlen, geteilt durch die Anzahl der Zahlen. Umgangssprachlich ist der arithmetische Mittelwert der übliche Mittelwert oder der Durchschnitt. Im Allgemeinen kann man nur das geometrische Mittel der positiven Zahlen nehmen. |
| Das geometrische Mittel als Definition ist die n-te Wurzel aus dem Produkt der n Einheiten der
Daten. Zum Beispiel ist das geometrische Mittel von 5, 7, 2, 1 dann (5 × 7 × 2 × 1)1/4 = 2,893. Oder auch exp [(ln (5) + ln (7) + ln (2) + ln (1)) / 4] = 2,893. |
Geometrisches Mittel
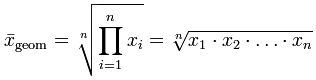
Arithmetisches Mittel
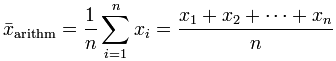
Berechnen der -3 dB Grenzfrequenzen f1 und f2, wenn die Mittenfrequenzund der Q-Faktor gegeben ist.
Geometrisches Mittel mehrerer Zahlen
|
Definition des geometrischen Mittels: Das Geometrische Mittel ist ein Zahlendurchschnitt, der den arithmetischen Mittelwert bildet. Das geometrische Mittel ist nur für Gruppen von positiven reellen Zahlen definiert. Dieses wird durch Multiplikation aller Zahlen berechnet (die Anzahl der Zahlenwerte ist n); dabei wird die n-te Wurzel aus dem Produkt gebildet. Ein typisches Beispiel - bei der das geometrische Mittel die richtige Wahl ist - ist die Mittelung von Wachstumsraten. Formel: Geometrisches Mittel = ((x1)(x2)(x3) ... (xn))1/n wobei x = Einzelwertung und n = Stichprobenumfang (Anzahl der Werte) ist. Beispiel für das Finden des geometrischen Mittels von 1, 2, 3, 4, 5. Schritt 1: n = 5, die Gesamtzahl der Werte. Suche 1 / n. 1 / n = 0.2 Schritt 2: Finden des geometrischen Mittelwerts nach der Formel: [(1) (2) (3) (4) (5)]0,2 = 1200,2 Geometrisches Mittel = 2,60517 Dieses Beispiel führt zum manuellen Berechnen des geometrischen Mittelwerts. Definition des arithmetischen Mittelwerts: Der arithmetische Mittelwert wird allgemein auch Durchschnitt genannt. Der Durchschnitt wird als die Summe aller gegebenen Elemente definiert, die durch die Gesamtzahl der Elemente geteilt wird. Formel: Arithmetisches Mittel = Summe der Elemente / Anzahl von Elementen = (a1 + a2 + a3 + ... + an) / n Beispiel um das arithmetische Mittel der Zahlen 3,5,7 zu finden. Schritt 1: Die Summe der Zahlen ist: 3 + 5 + 7 = 15 Schritt 2: Die Gesamtzahl der Elemente ist: 3 Zahlen. Schritt 3: Das arithmetische Mittel ist: 15 / 3 = 5 |
| zurück |
Suchmaschine |
Startseite |