

| Deutsche Version |
| To get a feeling for the heard sound quantities in decibels (dB), look at the table below which gives values for the sound levels of common sounds in our environment. Also shown are the corresponding sound pressures and sound intensities with the absolutely necessary measuring of the distance. From these we can see that the decibel scale gives numbers in a much more manageable range. Sound pressure levels are measured without weighting filters. |
| Avoid using the psychoacoustical terms loudness perception and volume. This subjective sound-sensation is not clearly measurable without ambiguity. The term "loudness" or "volume" is a problem because it belongs to psycho- acoustics and this personal feeling is not correct definable. Loudness as a psychological correlate of physical strength (amplitude) is also affected by parameters other than sound pressure, including frequency, bandwidth, spectral composition, information content, time structure, and the duration of exposure of the sound signal. The same sound will not create the same loudness perception by all individuals (people). |
| As psycho-acoustic parameters to describe the "loudness" there is the "loudness level" with the unit phon and the "loudness" with the unit sone. |
| The values are averaged and can differ about ±10 dB. With sound pressure p is always meant the root mean square value (RMS) of the sound pressure, without extra announcement. The amplitude of the sound pressure means the peak value. The sound pressure (RMS) is the most important quantity in sound measurement. Our hearing is a sound pressure receptor, or a sound pressure sensor, because the eardrums (tympanic membranes) are moved by the sound pressure as a sound field quantity. That is the important effect of the excess sound pressure. It is not an energy receiver! When listening to music, forget the sound intensity as energy quantity. The perceived sound consists of periodic acoustic pressure vibrations (sound pressure) which are superimposed on the surrounding static air pressure of 101 325 Pascal (mean atmospheric pressure). The sound is the change of sound pressure p, which is measured in pascal. 1 Pa ≡ N/m2 ≡ 1 J / m3 ≡ 1 kg / (m·s2). Usually p is the RMS value. |
| Table of sound levels L (loudness of noise) with corresponding sound pressure and sound intensity |
|
|
| Wrong question: "Jackhammer. How many dBs?" The distance is missing! Notice: A given sound level without a given distance is really useless. A typical question: How "loud" is 15 dB? Is there a distance from the source? |
| Sound pressure p (RMS) as Sound field quantity: The auditory threshold is used as the reference sound pressure p0 = 20 µPa = 2 × 10−5 Pa. The threshold of hearing corresponds to the sound pressure level Lp = 0 dB at f = 1 kHz. Sound intensity I as Sound energy quantity: The auditory threshold is calculated as the reference sound intensity I0 = 10−12 W/m2. The threshold of hearing corresponds also to the sound intensity level LW = 0 dB at f = 1 kHz. Sound pressure p = √ (I × Z0) Sound intensity I = p2 / Z0 acoustic impedance Z0 = 400 N·s/m3 |
What does sound level mean?
| A reduction of the sound power level of the sound source by 6 dB is resulting in a reduction of the sound pressure level and the sound intensity level at the location of the receiver by also 6 dB, even if the sound power drops to a factor of 0.25, the sound pressure drops to a factor of 0.5 and the sound intensity drops to a factor of 0.25. The reference value for the sound level was chosen so that with a characteristic acoustic impedance of Z0 = ρ · c = 400 N·s/m3 the sound intensity level results in the same value as the sound pressure level. We therefore simply speak of the "sound level" and leave it open whether sound pressure level or sound intensity level is meant.
|
| The sound level depends on the distance between the sound source and the place of measurement, possibly one ear of a listener. The sound pressure level Lp in dB without the given distance r to the sound source is meaningless. Unfortunately this error (unknown distance) is often to find. Many users really wrongly believe that a sound source must have a fixed dB value; e.g. jackhammer = 110 dB and jet plane = 130 dB. Distance ??? No distance, then forget the decibel value! The threshold of pain, depending on the frequency composition and the sensitivity of the tested person, is to find between 120 dB and 140 dB. |
| There is no noise decrease or sound drop per meter. We get a sound level drop of 6 dB per doubling of distance. |
|
Sound power or sound power level has nothing to do with the distance from the sound source. Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. |
| What is loud? Noise is a sound that disturbs or harms. |
| What we condemn as noise depends not only on the noise level. There are social, physical and psychological factors. Besides the type of noise and personal noise sensitivity there are the expectations of a person which is crucial to its assessment of noise. The "desired" noise is not the classification in 'noisy' or 'too loud'. Kurt Tucholsky wrote: "Our own dog does not make noise, it only barks" and "noise is the sound of the others." |
| What is the highest sound pressure possible? How many decibels is the loudest noise? |
Assumption: The greatest sound pressure that cannot be exceeded because |
| The total sound power is emitted by the sound source. Sound power levels are connected to the sound source and are independent of distance. Sound pressure levels vary substantially with distance from the source. |
| Sound pressure p in pascals (newtons per square meter) is not the same physical size as intensity J or I in watts per square meter. ... and the sound power (acoustic power) does not decrease with distance r from the sound source - neither with 1 / r nor as 1 / r2. |
| Sound Field Quantities Sound pressure, sound or particle velocity, particle displacement or displacement amplitude, (voltage, current, electric resistance). Inverse Distance Law 1/r |
Sound Energy Quantities Sound intensity, sound energy density, sound energy, acoustic power, (electrical power). Inverse Square Law 1/r² |
Sound pressure, Sound intensity and their Levels
| The following calculator shows the often desired direct conversion of sound pressure to sound intensity and vice versa with the specific acoustic impedance of air Z0 = 400 N·s/m3. |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| The sound pressure level in the air matchthe sound intensity level when we choose a reference sound characteristic impedance of Z0 = 400 N·s/m³. This is not the case with the distance independent sound power level. |
Source of disturbance - Musical instrument? Sound power (German)?
Sound pressure levels are not sound power levels (German)
| There is no "dBA" value given as threshold of human hearing. These values are not given as dBA, but as dBSPL, that means without any weighting filter. |
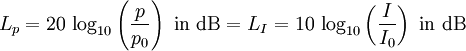 |
|
The sound field quantity as sound pressure p acting on the tympanic membranes of the ears is generally relevant to the subjective sensation of sound. When it comes to our ears and hearing, it is recommended to avoid the less appropriate expressions of the sound energy quantities such as sound power and sound intensity aside. As sound engineers let us care while listening especially to the sound pressure, or the sound pressure levelas sound field quantity. The architectural acoustics absolutely needs the sound energy sizes. In this region of calculation the "artistic ears" are less switched on. So we are just listening to the sound pressure, or the sound pressure level SPL. The sound pressure level decreases in the free field with 6 dB per distance doubling. That is the 1/r law. Often it is argued the sound pressure would decrease after the 1/r2 law (inverse square law). That's wrong. The sound pressure in a free field is inversely proportional to the distance from the microphone to the source. p ~ 1/r. |
How does the sound decrease with increasing distance?
Damping of sound level with distance
Relation of sound intensity, sound pressure and distance law:
|
| Note: The often used term "intensity of sound pressure" is not correct. Use "magnitude", "strength", "amplitude", or "level" instead. "Sound intensity" is sound power per unit area, while "pressure" is a measure of force per unit area. Intensity (sound energy size) is not equivalent to pressure (sound field size). |
| dB scale for field sizes, like volts and sound pressures |
 |
| ratio |
| The sound pressure is the force F in newtons N of a sound on a surface area A in m2 perpendicular to the direction of the sound. The SI-unit for the sound pressure p is N/m2 = Pa. p ~ 1/r. |
How to measure sound pressure?
Sound (pressure) level meter - SPL = Sound Pressure Level
 |
| By the way, sellers always want us to buy a sound pressure level meter with digital display. But much better, however, is an analogue-to-read display - as in this figure. |
| Note - Comparing dBSPL and dBA: There is no conversion formula for measured dBA values to sound pressure level dBSPL or vice versa. That is only possible measuring one single frequency. There is no "dBA" curve given as threshold of human hearing. The weighted sound level is neither a physiological nor a physical parameter. |
| Pro audio equipment often lists an A-weighted noise spec – not because it correlates well with our hearing – but because it can "hide" nasty hum components that make for bad noise specs. Words to bright minds: Always wonder what a manufacturer is hiding when they use A-weighting. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
Readings of a pure 1 kHz tone should be identical, whether weighted or not.
How loud is dangerous?
Typical dbA levels
| 190 dBA | Heavy weapons, 10 m behind the weapon (greatest level) |
| 180 dBA | Toy pistol fired close to ear (greatest level) |
| 170 dBA | Slap on the ear, fire cracker explodes on shoulder, small arms |
| 160 dBA | Hammer stroke on brass tubing or steel plate at 1 m distance, airbag deployment very close at a distance of 30 cm (greatest level) |
| 150 dBA | Hammer stroke in a smithy at 5 m distance (greatest level) |
| 130 dBA | Loud hand clapping at 1 m distance (greatest level) |
| 120 dBA | Whistle at 1 m distance, test run of a jet at 15 m distance |
| Threshold of pain, above this fast-acting hearing damage in short action is possible | |
| 115 dBA | Take-off sound of planes at 10 m distance |
| 110 dBA | Siren *) at 10 m distance, frequent sound level in discotheques and close to loudspeakers at rock concerts, violin close to the ear of an orchestra musicians (greatest level) |
| 105 dBA | Chain saw at 1 m distance, banging car door at 1 m distance (greatest level), racing car at 40 m distance, possible level with music head phones |
| 100 dBA | Frequent level with music via head phones, jack hammer at 10 m distance |
| 95 dBA | Loud crying, hand circular saw at 1 m distance |
| 90 dBA | Angle grinder outside at 1 m distance |
| Over a duration of 40 hours a week hearing damage is possible | |
| 85 dBA | 2-stroke chain-saw at 10 m distance, loud WC flush at 1 m distance |
| 80 dBA | Very loud traffic noise of passing lorries at 7.5 m distance, high traffic on an expressway at 25 m distance |
| 75 dBA | Passing car at 7.5 m distance, un-silenced wood shredder at 10 m distance |
| 70 dBA | Level close to a main road by day, quiet hair dryer at 1 m distance to ear |
| 65 dBA | Bad risk of heart circulation disease at constant impact is possible |
| 60 dBA | Noisy lawn mower at 10 m distance |
| 55 dBA | Low volume of radio or TV at 1 m distance, noisy vacuum cleaner at 10 m distance |
| 50 dBA | Refrigerator at 1 m distance, bird twitter outside at 15 m distance |
| 45 dBA | Noise of normal living; talking, or radio in the background |
| 40 dBA | Distraction when learning or concentration is possible |
| 35 dBA | Very quiet room fan at low speed at 1 m distance |
| 25 dBA | Sound of breathing at 1 m distance |
| 0 dB | Auditory threshold |
| Note - Comparing dBSPL and dBA: There is no conversion formula for measured dBA values to sound pressure level dBC or dBSPL. That is only possible measuring one single frequency. There is no "dBA" curve given as threshold of human hearing. |
Also no dBC measured values can be converted to dBA values.
The frequency composition of the signal is not known.
| *) A small frequency region makes high volume; see: Loudspeaker efficiency versus sensitivity "Amateurs" frequently ask about the high dB values from a siren. They are satisfied with each mentioned dB value. But they are not interested on the important distance from the noise source. That shows that they are just "dummies". How loud is a siren? The closer you get with ears to the sound source, the louder it will be. Anyone who feels disturbed in his apartment from the noise of the neighbors thinks it must give a measurable value for "low volume", which may not exceeded by the neighbor. Since volume is a personal not measurable subjective sensation in the ears of the deranged, no decibel value for the low room volume was determined by the courts. Noise is always the produced annoying noise of others. There is no objective judicially accepted definition of a sound level in decibels of low volume basis. Rated sound is not specified in phones, but increasingly in dB (A). If in the measurement of the noise the distance to the measurement microphone is not specified, this information is worthless. This unfortunately happens quite often. The sound power level in dB ist not the sound pressure level (SPL) or the sound intensity level! This information is often not understood or seems to be confusing. |
From a dB-A measurement no accurate description of the expected noise volume
is possible.
Table of the Threshold of pain
What is the pain threshold? The point at which pain begins to be felt.
Following rounded values are given in various audio articles and books:
| Sound pressure level Lp |
Sound pressure p |
| 140 dBSPL | 200 Pa |
| 137.5 dBSPL | 150 Pa |
| 134 dBSPL | 100 Pa |
| 130 dBSPL | 63 Pa |
| 120 dBSPL | 20 Pa |
| The threshold of pain is known in acoustics as the lowest strength of a stimulus, that is perceived by the ear as painful. Because of the different sensitivity of people it cannot be given an accurate value. |
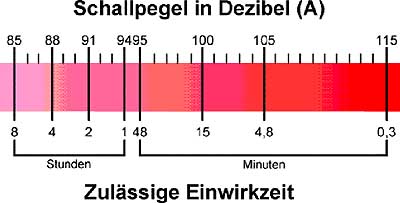 |
| Permissible Exposure Time Guidelines – Sound Pressure Level - SPL (Dose) How long can a person endure a certain noise level before hearing impairment occurs? |
| Sound Pressure Level | Sound pressure | Permissible Exposure Time |
| 115 dB | 11.2 Pa | 0.46875 minutes (~30 sec) |
| 112 dB | 7.96 Pa | 0.9375 minutes (~1 min) |
| 109 dB | 5.64 Pa | 1.875 minutes (< 2 min) |
| 106 dB | 3.99 Pa | 3.75 minutes (< 4 min) |
| 103 dB | 2.83 Pa | 7.5 minutes |
| 100 dB | 2.00 Pa | 15 minutes |
| 97 dB | 1.42 Pa | 30 minutes |
| 94 dB − − − − − − − − − − | 1.00 Pa − − − − − − | 1 hour − − − − − − − − − − − − − − |
| 91 dB | 0.71 Pa | 2 hours |
| 88 dB | 0.50 Pa | 4 hours |
| 85 dB | 0.36 Pa | 8 hours |
| 82 dB | 0.25 Pa | 16 hours |
| Accepted guidelines for recommended permissible exposure time for continuous time weighted average noise, according to NIOSH-AINSI and CDC. For every 3 dB sound pressure level (SPL) over 85 dB, the permissible exposure time is cut in half − before damage to our hearing can occur. NIOSH = National Institute for Occupational Safety and Health and CDC = Centers for Disease Control and Prevention. OSHA = Occupational Safety and Health Administration. NIOSH represents the use of an 8-hour exposure of noise at 85 dBA and a 3 dBA doubling rate, to determine the noise dose. OSHA represents the use of an 8-hour exposure of noise at 90 dBA and a 5 dBA doubling rate, which does not protect many workers from hearing loss over their whole working lifetime. This may not represent a worldwide view of the subject. Noise is an increasing public health problem and can have the following adverse health effects: hearing loss, sleep disturbances, cardiovascular and psychophysiological problems, performance reduction, annoyance responses, and adverse social behaviour. A person feels and judges sound events by exposure time, spectral composition, temporal structure, sound level, information content and subjective mental attitude. NIOSH represents the use of an 8-hour exposure of noise at 85 dBA and a 3 dBA doubling rate, to determine the noise dose. OSHA represents the use of an 8-hour exposure of noise at 90 dBA and a 5 dBA doubling rate, which does not protect many workers from hearing loss over their working lifetime. The answer to the question whether NIOSH or OSHA have more "correct" decibel values, may depend on the different perspective of the employer and the employee. Noise protection always costs money. |
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
Integration time of hearing
| Integration times of hearing: ca. 100 µs to 3 ms / 10 ms (sum localization) ca. 5 ms to 10 ms: echo threshold / masking ca. 10 ms coupling width ca. 50 ms pitch detection (recognition) ca. 250 ms sound smearing / quasi-stationary processes. |
The Psychoacoustic Loudness
| Note: Which increase corresponds to a doubling of the sound (factor = 2)? An increase of the sound level by 3 dB corresponds to a doubling of sound intensity. An increase of the sound level by 6 dB corresponds to a doubling of the sound pressure. An increase in the sound level by 10 dB corresponds to the sensation of double the "volume". The subjective perceived "volume" or "loudness level" and the artificial term "loudness" has not to be mixed with the objective measure of sound pressure as sensation size of the human sense of hearing. The sound pressure as a sound field size is not the same as the sound intensity as sound energy size. Psychoacousticians tell us that a level increase of 10 dB should result in an impression of doubling the loudness (volume). If we have 6 violins as the initial source, then we need 10 times the violins, or 60 violins to double the psychoacoustic volume (loudness). |
| Half loudness ≡ level −10 dB | Double loudness ≡ level +10 dB |
| Half sound pressure ≡ level −6 dB | Double sound pressure ≡ level +6 dB |
| Half power ≡ level −3 dB | Double power: ≡ level +3 dB |
| four times power ≡ level +6 dB | Ten times power ≡ level +10 dB |
| Double distance ≡ level −6 dB | Double sources (Double power) ≡ +3 dB |
| Note: For example, when the sound system with spaced loudspeakers delivers twice the sound pressure as "one" amplifier,the fourfold power is required. So we need to double the "sound pressure" for example, four parallel amplifiers of the same design. Frequently one hears the novice question: How much more speaker power do we need for double the "volume" (loudness)? This takes about ten times the power. |
Sound Level Comparison Chart and the Ratios
| Table of sound level dependence and the change of the respective ratio to subjective volume (loudness), objective sound pressure (voltage), and sound intensity (acoustic power) How many decibels (dB) change is double, half, or four times as loud? How many dB to appear twice as loud (two times)? Here are all the different ratios. Ratio means "how many times" or "how much" ... Doubling of loudness. |
| Subjectively perceived loudness (volume), objectively measured sound pressure (voltage), and theoretically calculated sound intensity (acoustic power) |
| Level Change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +60 dB | 64 | 1 000 | 1 000 000 |
| +50 dB | 32 | 316 | 100 000 |
| +40 dB | 16 | 100 | 10 000 |
| +30 dB | 8 | 31.6 | 1 000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - - - | - - - - - 1.0 - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 1/4 = 0.25 | 0.100 | 0.01 |
| −30 dB | 1/8 = 0.125 | 0.031 6 | 0.001 |
| −40 dB | 1/16 = 0.062 5 | 0.010 0 | 0.000 1 |
| −50 dB | 1/32 = 0.031 2 | 0.003 2 | 0.000 01 |
| −60 dB | 1/64 = 0.015 6 | 0.001 0 | 0.000 001 |
| Log. size | Psycho size | Field size | Energy size |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
The psycho-acoustic volume or loudness is a subjective sensation size.
|
Is a 10 dB or 6 dB sound level change for a doubling or halving of the loudness (volume) correct? About the connection between sound level and loudness, there are various theories. Far spread is still the theory of psycho-acoustic pioneer Stanley Smith Stevens, indicating that the doubling or halving the sensation of loudness corresponds to a level difference of 10 dB. Recent research by Richard M. Warren, on the other hand leads to a level difference of only 6 dB. *) This means that a double sound pressure corresponds to a double loudness. The psychologist John G. Neuhoff found out that for the rising level our hearing is more sensitive than for the declining level. For the same sound level difference the change of loudness from quiet to loud is stronger than from loud to quiet. It is suggested that the sone scale of loudness reflects the influence of known experimental biases and hence does not represent a fundamental relation between stimulus and sensation. *) Richard M. Warren, "Elimination of Biases in Loudness Judgments for Tones", 1970, Journal of the Acoust. Soc. Am. Volume 48, Issue 6B, pp. 1397 - 1403 and Richard M. Warren, "Quantification of Loudness", 1973, American Journal of Psychology, Vol 86 (4), pp. 807 - 825 John G. Neuhoff, "An adaptive bias in the perception of looming auditory motion", 2001, Ecological Psychology 13 (2) pp. 87 - 110 and John G. Neuhoff, "Perceptual Bias for Rising Tones", 1998, Nature, Volume 395, 10 September Citation: When known experimental biases were eliminated, half loudness was equal to half sound pressure level (−6 dB) from 45 to 90 dB. It follows that the determination of the volume (loudness) which is double as loud should not be dogmatically defined. More realistic is the claim: |
| A doubling of the sensed volume (loudness) is equivalent to a level change approximately between 6 dB and 10 dB. |
| Conversion of sound units (levels) Calculations of sound values and their levels Conversion of voltage V to dBm, dBu, and dBV |
| Question: What is the standard distance to measure sound pressure level away from equipment? There is really no standard distance for measuring dB (decibels). It depends on the size of the sound source and the sound pressure level. |
| Differentiate: Sound pressure p is a "sound field size" and sound intensity I is a "sound energy size". In teachings these terms are not often separated sharply enough and sometimes are even set equal. But I ~ p2. |
| Question: How does the sound power decrease with distance"? Answer: "April fool - The sound power does not decrease (drop) with distance from the sound source." Levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source. Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. A frequent question: "Does the sound power depend on distance?" The clear answer is: "No, not really." We consider sound fields in air which are described by the scalar quantity p (sound pressure) and the vector quantity v (sound velocity) as a sound field quantity. |
|
Note: The radiated sound power (sound intensity) is the cause and the sound pressure is the effect, where the sound engineer is particularly interested in the effect. The effect of temperature and sound pressure: Sound pressure and Sound power – Effect and Cause. |
| Acousticians and sound protectors (noise fighters) need the sound intensity (acoustic intensity) – but as a sound engineer and sound designer (ear people) you don't need that sound energy quantity. Who is involved in audio engineering, should rather take care of the sound field quantity, that is the sound pressure or the sound pressure level (SPL) as an effect at the eardrums of our hearing and on the diaphragms of the microphones, and the corresponding audio voltage and its voltage level. |
Sound pressure and Sound power − Effect and Cause
Ratio magnitudes and levels
| The decibel is defined as a 20 times logarithm of a ratio of linear sizes to each other and as a 10 times logarithm of a ratio of quadratic sizes to each other. Ratios of electric or acoustic sizes, such as electric voltage and the sound pressure is referred to as ratios (factors), such as reflection factor. Ratios of square sizes to one another, such as power and energy are called grades, such as efficiency. Logarithmically ratios of electric or acoustic sizes of the same unit, we express as measures such as transfer factor, or level, such as sound pressure level. Levels are measured in decibels - dB in short. |
| If the output voltage level is 0 dB, that is 100%, the level of −3 dB is equivalent to 70.7% and the level of −6 dB is equivalent to 50% of the initial output voltage. This applies to all field sizes; e.g. sound pressure. If the output power level is 0 dB, that is 100%, the level of −3 dB is equivalent to 50% and the level of −6 dB is equivalent to 25% of the initial output power. This applies to all energy sizes; e.g. sound intensity. Try to understand this. |
Conversion of sound pressure to sound power and vice versa
| The sound pressure changes depending on the environment and the distance from the sound source. In contrast, the sound power of a sound source is location-independent. Formulas for conversion: Acoustical power (sound power) Pac = I × Ain watts Sound intensity I = peff2 / Z0 in W/m2 = Pac / Ain W/m2 Perfused area A = 4 × π × r2 in m2 Distance measurement point from the sound source r in meters (has only meaning with sound pressure, not with sound power) Acoustic impedance of air Z0 = 413 N·s/m3 at 20 °C Sound pressure peff in Pa = N/m2 In point-like sound sources spherical areas A shall be inserted. Depending on the arrangement following sections are taken into account: Solid sphere - sound source anywhere in the room, Q = 1 Hemisphere - sound source on the ground, Q = 2 Quarter Sphere - sound source on the wall, Q = 4 Eighth sphere - sound source in the corner, Q = 8 Q = direction factor and area A = (4 × π × r2) / Q |
Compare Sound power level and sound pressure level
in a distance from the sound source
| A typical question: "What is the dB volume of a symphony orchestra?" Answer: "It really depends on the distance from the listener to the orchestra." To name the distance is often "forgotten". They want to hear only a decibel number. But only a dB number is really senseless. |
| There is a constant uncertainty of the answer to the question: "How many decibels (dB) are doubling a sound"? or "What is twice the sound?" Answer: Doubling means the "factor 2". What does doubling of a "sound" mean? Doubling the (sound) intensity is obtained by an increase of the sound intensity level of 3 dB. Doubling the sound pressure is obtained by an increase of the sound pressure level of 6 dB ● Doubling the loudness feeling is obtained by an increase of the loudness level of about 10 dB. Double or twice the power = factor 2 means 3 dB more calculated power level (sound intensity level). Double or twice the voltage = factor 2 means 6 dB more measured voltage level (sound pressure level) ● Double or twice the loudness = factor 2 means 10 dB more sensed loudness level (psycho acoustic). |
| Simple rule of thumb: When working with power, 3 dB means double (twice) the factor and 10 dB means 10-fold. When working with voltage or current, 6 dB means double (twice) the factor and 20 dB means 10-fold. |
| Some information about Hearing Level (HL) Pure-tone audiometric thresholds are expressed in "dB HL". |
| Frequency | dB SPL | dB HL |
| 250 Hz | +15.0 | 0.0 |
| 500 Hz | +9.0 | 0.0 |
| 1000 Hz | +3.0 | 0.0 |
| 2000 Hz | −3.0 | 0.0 |
| 4000 Hz | −4.0 | 0.0 |
| 8000 Hz | +13.0 | 0.0 |
| In sound engineering there is no power matching or impedance matching. In audio we use only voltage bridging or high impedance bridging. Please read the following information carefully: "8 Ohm Output" and "150 Ohm Input" − What is that? |
| Theshold | Sound pressure level (SPL) at a frequency of | ||||
| Frequency | 8 Hz | 10 Hz | 12,5 Hz | 16 Hz | 20 Hz |
| Auditory threshold of hearing | 103 dB | 95 dB | 87 dB | 79 dB | 71 dB |
| Auditory threshold of perception | 100 dB | 92 dB | 84 dB | 76 dB | 68 dB |
| back |
Search Engine |
home |