

| Deutsche Version |
| Incoherent or noncoherent means the signals of the overdubbed channels are irrelative like a violin and a trumpet, that means having no correlative relationship. Sometimes we say uncorrelated when we mean incoherent. Given two incoherent sources their combined effect is the sum of their acoustic power. |
| Fill in as many sound level boxes as necessary (max 10) and then click the calculate bar, to get the calculated sum. Provided, that each sound source has its own random phasing. |
A program to combine as much as thirty (30) noise sources
Conversion of sound pressure level to sound pressure and sound intensity
Adding Amplitudes and Levels (coherent and incoherent)
The ten octave bands of our hearing range
The formula for the sum level of sound pressures of n incoherent radiating sources is
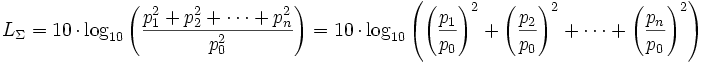
The reference sound pressure p0 is 20 µPa = 0.00002 Pa = 2 × 10−5 Pa (RMS) ≡ 0 dB.
From the formula of the sound pressure level we find
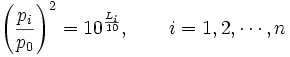
This inserted in the formula for the sound pressure level to calculate the sum level shows
![]()
LΣ = Total level and L1, L2, ... Ln = sound pressure level of the separate sources in dBSPL.
Incoherent means: lacking cohesion, connection, or harmony. It is not coherent.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3.01 | 2.54 | 2.12 | 1.76 | 1.46 | 1.19 | 0.97 | 0.79 | 0.64 | 0.51 | 0.41 |
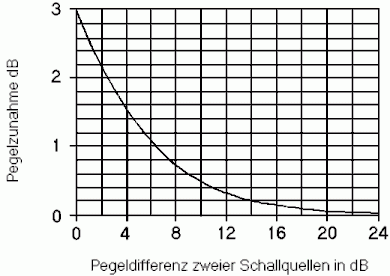 Level difference between the two sound sources |
![]()
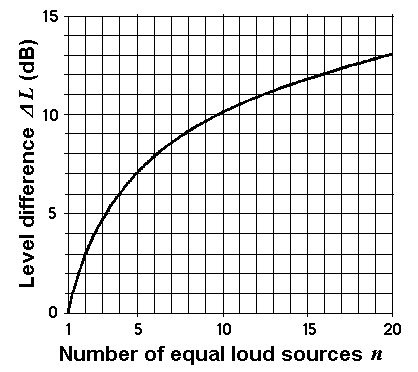
Adding of equal loud incoherent sound sources
 |
|
||||||||||||||||||||||||||||||
Formulas: Δ L = 10 × log n or n = 10(ΔL/10)
Δ L = level difference; n = number of equal loud sound sources.
| n = 2 equally loud incoherent sound sources result in a higher level of 10 × log10 2 = +3.01 dB compared to the case that only one source is available. n = 3 equally loud incoherent sound sources result in a higher level of 10 × log10 3 = +4.77 dB compared to the case that only one source is available. n = 4 equally loud incoherent sound sources result in a higher level of 10 × log10 4 = +6.02 dB compared to the case that only one source is available. n =10 equally loud incoherent sound sources result in a higher level of 10 × log10 10 = +10.00 dB compared to the case that only one source is available. |
Adding (combining) levels of equal loud sound sources
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
The total level in dB is the level of one sound source plus the increase of level in dB.
| Example: The measurable noise of a motorcycle is at a certain distance
60 dB (A). How big is the total level of 4 motorcycles with the same volume? Solution: 60 dB (A) + 10 log 4 = 60 + 6 = 66 dB (A). If you are doing noise measurements of motorcycles you should at least consider the "honesty" of the dBA-readings without low frequencies. |
| You can easily add up coherent and incoherent sound level and sound pressure values. It is often desired to add the psychoacoustic perceived loudness or volume. See: |
| How many decibels (dB) level change is double, half, or four times as loud?
How many dB to appear twice as loud (two times)? Here are all the different ratios. Ratio means "how many times" or "how much" ... Doubling of loudness. |
| Level change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31.6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 0.25 | 0.100 | 0.01 |
| −30 dB | 0.125 | 0.0316 | 0.001 |
| −40 dB | 0.0625 | 0.0100 | 0.0001 |
| Log. size | Psycho size | Field size | Energy size |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
| Ratio | Change in Sound Loudness Level |
Change in Sound |
Change in Sound Power Level |
| 20 | +43.22 dB | +26.02 dB | +13.01 dB |
| 15 | +39.07 dB | +23.52 dB | +11.76 dB |
| 10 | +33.22 dB | +20 dB | +10 dB |
| 5 | +23.22 dB | +13.98 dB | +6.99 dB |
| 4 | +20 dB | +12.04 dB | +6.02 dB |
| 3 | +15.58 dB | +9.54 dB | +4.77 dB |
| 2 | +10 dB | +6.02 dB | +3.01 dB |
| - - - - - 1 - - - - - | - - - - ±0 dB - - -- - | - - - - ±0 dB - - - -- | - - - ±0 dB - - -- - |
| 1/2 = 0.5 | −10 dB | −6.02 dB | −3.01 dB |
| 1/3 = 0.3333 | −15.58 dB | −9.54 dB | −4.77 dB |
| 1/4 = 0.25 | −20 dB | −12.04 dB | −6.02 dB |
| 1/5 = 0.2 | −23.22 dB | −13.98 dB | −6.99 dB |
| 1/10 = 0.1 | −33.22 dB | −20 dB | −10 dB |
| 1/15 = 0.0667 | −39.07 dB | −23.52 dB | −11.76 dB |
| 1/20 = 0.05 | −43.22 dB | −26.02 dB | −13.01 dB |
Noise
| Noise is annoying, harassing and unwanted sound. It is not a physical phenomenon, but
only mental processes change a sound to noise. There are a number of definitions of noise. Important ones are: 1 - the acoustic ratio that characterize the noise and by measurable physical sizes, such as the amplitude or the sound pressure level, frequency, and the time behavior of the sound, can be described. 2 - the situational ratio, i.e. location, time and situation in which the person is situate during the occurrence of the noise, and the relation to the activities, intentions and the current being of the person who is exposed to the noise. 3 - the personal ratio of the person who is exposed to the noise, with their acquired cognitive and emotional implications for the sound source. The fact that noise is not only dependant on physically measurable sizes, but "of more", makes the derivation of methods and calculation methods for the objective description to a problem and explains the problems of noise control, which are often found between the measured noise values and the perceived harassment. Kurt Tucholsky wrote aptly: "Our own dog does not make noise, it only barks. |
| Castrated sound level values in weighted dBA are added the same way like sound level values in unweighted dB. |
| Pro audio equipment often lists an A-weighted noise spec – not because it correlates well with our hearing – but because it can "hide" nasty hum components that make for bad noise specs. Words to bright minds: Always wonder what a manufacturer is hiding when they use A-weighting. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
Formulas for working with sound
| 1 pascal (Pa) = 1 newton/m2 = 10 dyne/cm2 = 10 microbar ≡ 94 dB SPL (Sound Pressure Level) Sound Pressure Level (SPL) Sound pressure level Lp = 20 × lg (p / p0) in decibels (dB), where p is the measured pressure as sound field size and p0 is the reference pressure in the same system of units. p0 = 20 micropascals or micronewtons/m2 = 0.00002 Pa = 0.0002 microbar or dyne/cm2. This reference sound pressureas a sound field size corresponds to a sound wave in free air with an acoustic pressure of p0 = 0.00002 Pa (N/m²). Sound Intensity Level (SIL) or Acoustic Intensity Level Sound intensity level LI = 10 × lg (I / I0) in decibels (dB), where I is the measured intensity as sound energy size and I0 is the reference sound intensity in the same system of units. I0 = 10−12 watt per m2. This reference sound intensity as a sound energy size corresponds to a sound wave in free air with an acoustic intensity (energy) of I0 = 10−12 watt/m2. |
What does sound level mean?
A reduction of the sound power level of the sound source by 6 dB is resulting in a reduction of the sound
pressure level and the sound intensity level at the location of the receiver by also 6 dB, even if the sound
power drops to a factor of 0.25, the sound pressure drops to a factor of 0.5 and the sound intensity drops
to a factor of 0.25. The reference value for the sound level was chosen so that with a characteristic acoustic
impedance of Z0 = ρ · c = 400 N·s/m3 the sound intensity level results in the same value as the sound
pressure level. We therefore simply speak of the "sound level" and leave it open whether sound pressure
level or sound intensity level is meant.
|
| back |
Search Engine |
home |