| Formeln | |
|
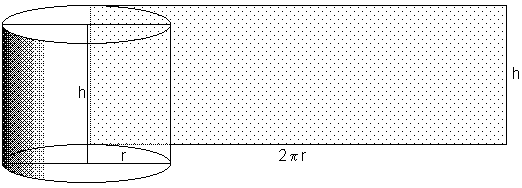
Grundfläche (Kreis) |
K = p · r² u = 2 · p · r |
| Mantelfläche | M = h · u = 2 · p · r · h |
| Oberfläche |
A = 2 · K + M A = 2 · p · r · (h + r) |
| Volumen | V = K · h = p · r² · h |
Weitere geometrische Berechnungen:
Dreieck | Rechteck | Quadrat | Kreis | Kugel | Quader | Kegel | Würfel | Flächen
- Horizontaler Zylindertank - Aufgabe mit Lösung
| Es geht um die zu bestimmende Rest-Füllmenge in einem Tank, bei dem die Füllstandshöhe mit h = 0,37 m bekannt ist. Der Tank ist ein horizontal-liegender Zylinder. Grundkreisradius der Seitenfläche: r = 0,80 m und Zylinderlänge: z = 3,50 m. Um die Rest-Füllmenge V(h) bis zur Füllstandshöhe h zu berechnen, muss man die Fläche A(h) des von der Flüssigkeit benetzten Teils des Grundkreises mit der Zylinderlänge z multiplizieren: Das Volumen der Rest-Füllmenge ist V(h) = A(h) · z. Die zu berechnende Fläche A ist ein Kreissegment.  Wenn man das Verhältnis  einführt, kann man kürzer schreiben: Die Arcuscosinuswerte sind im Bogenmaß (RAD) zu berechnen. α im Bogenmaß (RAD) = α° · π / 180. Die gesuchte Rest-Füllmenge im Tank ist: V(h) = A(h) · z. Bei einer Füllstandshöhe von h = 0,37 m ergibt sich eine Rest-Füllmenge im Tank von: V = 1,232162257 m3, das sind 1232,162257 Liter.  |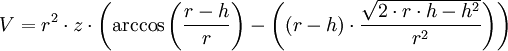
Rechenweg siehe auch: Horizontal Cylindrical Tank Calculation
zurück  |
Suchmaschine  |
Startseite  |