Dreieck Höhe Winkel Seite Dreiecks-Berechnung Dreieck Fläche Umfang online - sengpielaudio
 
● Dreiecks-Berechnung - Berechnungen rund um das Dreieck ●
 
Ein Dreieck stellt üblicherweise eine Fläche dar. Wer nach dem Volumen
eines "Dreiecks" fragt, der sollte noch einmal gründlich nachdenken.
 
DieKongruenzsätze besagen, dass ein Dreieck eindeutig konstruiert werden
kann, wenn eine dieser Kombinationen an gegebenen Maßen vorliegt:
 
  • eine Seite und zwei Winkel (SWW, WSW oder WWS)
  • zwei Seiten und der der größeren Seite gegenüberliegende Winkel (SSW oder WSS)
  • zwei Seiten und der eingeschlossene Winkel (SWS)
  • drei Seiten (SSS)
 
Drei Werte sind ohne Einheiten einzugeben. Der Rest wird berechnet.

Seite a =  Seite b =  Seite c = 
Winkel α =   °  Winkel β =   °  Winkel γ =   ° 
Höhe ha =  Höhe hb =  Höhe hc = 
Umfang u =  Fäche A =    
1.Lösung zuerst anzeigen? 2.Lösung zuerst anzeigen?
Beliebiges Dreieck 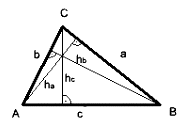Dreieck 01 - sengpielaudioDreieck 02 - sengpielaudio
Rechtwinkeliges Dreieck Dreieck 03 - sengpielaudioDreieck 04 - sengpielaudio
Satz des Pythagoras Dreieck 05 - sengpielaudio
Höhensatz Dreieck 06 - sengpielaudio
Kathetensatz Dreieck 07 - sengpielaudio   Dreieck 08 - sengpielaudio
Gleichseitiges Dreieck

Dreieck 09 - sengpielaudio

Dreieck 10 - sengpielaudio   Dreieck 11 - sengpielaudio
Dreieck 12 - sengpielaudio   Dreieck 13 - sengpielaudio
Formel von Heron

Flächenberechnung
wenn 3 Seiten bekannt sind

(gilt für jedes Dreieck)
 Dreieck 14-1 - sengpielaudio mit Dreieck 14-2 - sengpielaudio oder Dreieck 14A - sengpielaudio
Umkreisradius (gilt für jedes Dreieck)
Dreieck 15 - sengpielaudio
Inkreisradius (gilt für jedes Dreieck)
Dreieck 16 - sengpielaudio

 Heron's Formel zur Flächenberechnung eines Dreiecks 
A = √[s(s-a)(s-b)(s-c)], s = (a+b+c)/2 oder Umfang/2
Seite Länge
a =
b =
c =
       
Fläche A des
Dreiecks =
s = (a+b+c)/2 =

Cosinussatz:
a = √ (b2 + c2 - 2 b c cos α)
b = √ (a2 + c2 - 2 a c cos β)
c = √ (a2 + b2 - 2 a b cos γ)

Aufgelöst nach Winkeln:
α = arccos [(-a2 + b2 + c2)/(2 b c)]
β = arccos [(-b2 + a2 + c2)/(2 a c)]
γ = arccos [(-c2 + a2 + b2)/(2 a b)]

arccos [ ] = arctan √[(1 - X2)/X], wobei ist X = cos [ ]

Sinussatz:
a / sin α = b / sin β = c / sin γ

Satz der Winkelsumme:
α + β + γ = 180

Umrechnung von Grad (°) in Bogenmaß (radians):
Grad = Bogenmaß · (180 / 3,141593)
Bogenmaß = Grad · (3,141593 / 180)

Weitere Berechnungen:

Kreis | Rechteck | Quadrat | Kugel | Würfel | Quader | Zylinder | Kegel | Flächen

zurück zurück Suchmaschine weiter Startseite start