| English version |  |
 |
| Frage: Wie lautet die Formel für die Phase einer Sinuswelle? Es gibt keine Phase einer Sinuswelle. Eine Sinuswelle hat keine Phase. Eine Phase kann nur zwischen zwei Sinuswellen auftreten. Zwei Sinusschwingungen sind gegeneinander phasenverschoben, wenn die Zeitpunkte ihrer Nulldurchgänge nicht übereinstimmen. |
| Das Wort Phase ist eindeutig allein für zwei Sinuswellen oder Sinussignale definiert, jedoch nicht für Musiksignale oder Lärm. Alle Equalizer verschieben die Phase mit der Frequenz. Ohne einen festen Bezugspunkt ist keine "Verschiebung" möglich. Besondere Tricks: z. B. 90° filter mit zwei Allpässen. Phasen sind eigentlich immer Phasendifferenzen. Verpolung ist Polaritätswechsel und niemals Phasenverschiebung auf der Zeitachse t. Sinusförmige Wellenformen der gleichen Frequenz können eine Phasendifferenz haben. Bei einer Phasenverschiebung des Phasenwinkels φ in Grad ist immer anzugeben zwischen welchen Sinussignalen diese sein soll. So kann es beispielsweise eine Phasenverschiebung zwischen den Zweikanalsignalen L und R geben, zwischen einem Eingangs- und Ausgangssignal, zwischen der Spannung und dem Strom oder zwischen dem Schalldruck p und der Luftteilchenschnelle v. |
Was ist eigentlich eine Amplitude?
|
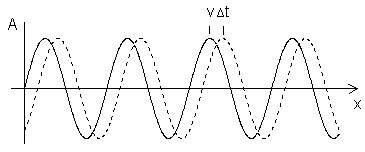
Eine komplette Schwingung der Welle ist verbunden mit der Winkelgeschwindigkeit im Bogenmaß von 2 π.  Die Phase φ ist der Winkel eines Signalteils, sie wird in Winkelgrad angegeben und stellt den Bezug zu dem Referenzwert des kompletten Signals dar. Bei periodischen Signalen beträgt der gesamte Phasenwinkel einer Periode 360 Grad und entspricht der Periodendauer. Eine typische Frage: Was ist bei einer Frequenz die Phase oder der Phasenwinkel? Eine typische Frage: Was ist die Frequenz und der Phasenwinkel einer Sinuswellenform? Kann eigentlich "ein" Signal eine Phase haben? "Im deutschen Sprachgebrauch erscheint es manchmal so, als ob zwischen Phase und "faseln" ein Zusammenhang besteht." (Joerg Wuttke). Zwei gleiche Wellen haben eine "Phase" oder einen Phasenwinkel von φ = 0 Grad. Ist die Frequenz = 0 Hz, dann liegt keine Wechselspannung vor – das ist einfach Gleichstrom. Es kann dann auch kein Phasenwinkel vorhanden sein. |
Was hat denn Laufzeit mit Phase zu tun?
| Der Zusammenhang zwischen dem Phasenwinkel φ° im Gradmaß (deg), der Verzögerung Δ t und der Frequenz f ist: Phasenwinkel (deg)  Zeitverschiebung oder Laufzeitdifferenz  Frequenz  λ = c / f und c = 343 m/s bei 20°C. Der Zusammenhang zwischen dem Phasenwinkel φBogen im Bogenmaß (rad), der Verzögerung Δ t und der Frequenz f ist: Phasenwinkel (rad)  Zeitverschiebung oder Laufzeitdifferenz  Frequenz  Laufzeit = Umweg / Schallgeschwindigkeit |
Die Laufzeit des Schalls pro Meter
Die Wirkung der Temperatur auf die Laufzeit Δ t
Die Abhängigkeit der Schallgeschwindigkeit allein von der Temperatur der Luft
| Temperatur der Luft °C |
Schallgeschwindigkeit c in m/s |
Zeit pro 1 m Δ t in ms/m |
| +40 | 354,9 | 2,817 |
| +35 | 352,1 | 2,840 |
| +30 | 349,2 | 2,864 |
| +25 | 346,3 | 2,888 |
| +20 | 343,4 | 2,912 |
| +15 | 340,5 | 2,937 |
| +10 | 337,5 | 2,963 |
| +5 | 334,5 | 2,990 |
| ±0 | 331,5 | 3,017 |
| –5 | 328,5 | 3,044 |
| –10 | 325,4 | 3,073 |
| –15 | 322,3 | 3,103 |
| –20 | 319,1 | 3,134 |
| –25 | 316,0 | 3,165 |
| Tontechniker nehmen gerne die einfache Faustformel: Für r = 1 m Wegstrecke braucht der Schall in Luft rund t = 3 ms. Δ t = r / c und r = Δ t · c Schallgeschwindigkeit c = 343 m/s bei 20°C. |
| Phasendifferenz φ° (deg) |
Phasendifferenz φBogen (rad) |
Frequenz f |
Wellenlänge λ = c / f |
| 360° | 2 π = 6,283185307 | 2000 Hz | 0,171 m |
| 180° | π = 3,141592654 | 1000 Hz | 0,343 m |
| 90° | π / 2 = 1,570796327 | 500 Hz | 0,686 m |
| 45° | π / 4 = 0,785398163 | 250 Hz | 1,372 m |
| 22,5° | π / 8 = 0,392699081 | 125 Hz | 2,744 m |
| 11,25° | π /16= 0,196349540 | 62,5 Hz | 5,488 m |
Umrechnung: Bogenmaß (rad) in Winkelgrad (deg) und zurück
Phasenlaufzeit: φ° = 360 · f · Δ t
Bei Laufzeitstereofonie ist Δ t = a · sin α / c
Frequenz f = φ° / 360 · Δ t
Phasenwinkel (deg) φ = Verzögerung (Delay) Δ t · Frequenz f · 360
Setzt man die Laufzeitdifferenz Δ t = Wegstrecke a / Schallgeschwindigkeit c, dann ist die
Phasendifferenz φ° = Wegdifferenz a · Frequenz f · 360 / Schallgeschwindigkeit c
Bitte zwei Werte eingeben, der dritte Wert wird berechnet.
Siehe auch: Laufzeitdifferenz und Phasenverschiebung
| Von Lord Rayleigh (John William Strutt, 3. Baron Rayleigh, 1907) wurde die Duplex-Theorie angegeben. Diese Theorie trägt zum Verstehen des Vorgangs beim "natürlichen Hören" beim Menschen bei. Es gibt die Erkenntnis, dass die interauralen Laufzeitdifferenzen ITD bei Frequenzen unterhalb 800 Hz als Phasendifferenzen (Phasenverschiebung) IPD bei der Richtungslokalisation als Ohrsignale bedeutsam sind, während bei Frequenzen oberhalb von 1600 Hz sich allein die interauralen Pegeldifferenzen ILD auswirken. Die Phasendifferenz kann für einzelne Frequenzen berechnet werden. Zwischen den Ohren beträgt die maximale Verzögerung (Delay) 0,63 ms - als ITD bzw. Δ t. |
Schaltplan: Phasenschieber für Phasenwinkel von φ = 0° bis 180°
Spannungsvektoren des Phasenschiebers
|
Für R = 0 Ohm wird Ua = Ue. Der Ausgang darf nicht niederohmig belastet werden.
Hiermit kann man Einzelfrequenzen (Sinus) in der Phase verschieben.
Das geht jedoch niemals bei Musik mit dieser Schaltung.
Zwei Sinusspannungen, um φ = 45° phasenverschoben
 |
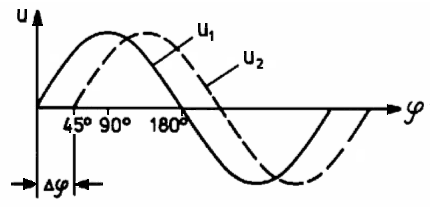Bedingungen für verzerrungsfreie Übertragung
Aus Schoeps - Jörg Wuttke: "Mikrofonbuch Kap. 7"
 |
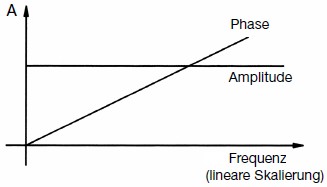| Während die Forderung nach konstantem Frequenzgang einleuchtet, ist der lineare Phasengang eher erklärungsbedürftig. Es gibt Toningenieure, die vom idealen Phasengang erwarten, dass er so konstant verläuft wie der Amplitudenfrequenzgang. Das trifft nicht zu. Zunächst muss die Phase bei 0° beginnen, denn der Grenzfall tiefster Frequenzen endet bei 0 Hz, also bei Gleich-Verhältnissen. Einen Phasenwinkel zwischen beispielsweise zwei Gleichspannungen gibt es nicht. Im weiteren Verlauf ist ein beliebig großer Phasenwinkel bei gegebener Frequenz ohne Bedeutung, sofern er nur doppelt so groß ist bei doppelter Frequenz und dreimal so groß bei dreifacher Frequenz, usw. |
Von David Moulton Laboratories
(About Comb Filtering, Phase Shift and Polarity Reversal)
 |
|
Das elektronische Äquivalent eines Signalflusses und seine verzögere Kopie summiert zu einemSignal. In diesem Falle betrachten wir die Verzögerung von 1 Millisekunde und den beiden gleichgroßen Pegeln bei Original und verzögertem Signal, die in den Mixer gehen bei einem Sinussignal von 1 kHz. |
 |
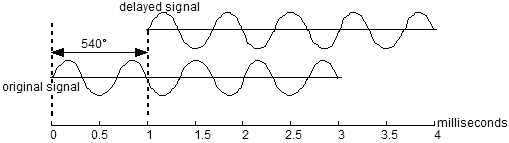| Ein Sinuston von 1500 Hz (Periode T = 0,667 ms) und sein verzögertes Abbild, bei 1 ms Verzögerung. Das sich daraus ergebende gemischte Signal wird ein Signal ohne Amplitude sein, was eine vollständige Auslöschung des Signals bedeutet. |
 |
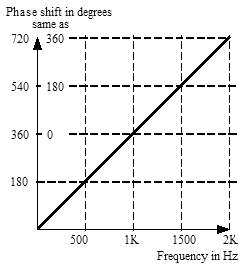| Die Phasenverschiebung für jede Frequenz mit einer Verzögerung von 1 Millisekunde. Die Diagonale zeigt die zunehmende Phasenverschiebung als Funktion der Frequenz. Wir sehen, dass die Phasenlage von 540° genau das Gleiche wie 180° ist. |
Verpolung ist keine Phasenverschiebung von 180°
| Ø (phi) = phase shift, phase shifting, phase difference, displacement of phase, phase lag, phase angle = Phasenverschiebung. Dieses Wort wird aber recht häufig falsch benutzt für: Polarity reversal = Pol-Rev, voltage reversal = Verpolung oder Polaritätswechsel, Polaritätsumkehr. |
| "Es war die Nachtigall, und nicht die Lerche". Aus: Romeo und Julia, 3. Akt, 5. Szene, William Shakespeare. Es ist der Verpolungsschalter ("Pol-Rev") und nicht der Phasenschalter ("Phase-shift") It is the "POL-REV" button (polarity reversal) and not the "Phase" button 1. Generating a comb filter response 2. "Polarity" and "Phase" |
Polarität und Phase werden oft so benutzt, als ob sie das gleiche bedeuten. Das ist nicht der Fall.
Die "Phase Reverse Schalter" Ø ändert nichts an der Phase. Es kehrt die Polarität um.
| Verpolung ist keine Phasenverschiebung − Polarity reversal is no phase shift Verpolung, Invertierung (PolRev = polarity reversal) ist ein Begriff, der oft mit Phase Ø (phi) verwechselt wird, aber keine Phasenverschiebung oder zeitliche Verzögerung (Delay) enthält. Verpolung tritt auf, wenn wir die "Vorzeichen" der Amplitudenwerte eines Signals gegenüber einem anderen vertauschen. Im analogen Bereich kann dieses durch Invertierung eines Verstärkers, durch einen Übertrager, oder bei einer symmetrischen Leitung durch einfaches Vertauschen der Verbindungen von Pin 2 und 3 (XLR-Stecker) an einem Ende des Kabels geschehen. Im digitalen Bereich ist das einfach zu verändern, indem man im Audiodatenstrom alle Minus in Plus invertiert. |
Zwei Sägezahnschwingungen
 |
oben: Das originale Signal a/b (Sägezahn) mitte: Das phasenverschobene Signal (180°) als um T/2 zeitlich verschobener Sägezahn unten: Das verpolte (gegenpolige oder invertierte) Signal (b/a), an der Zeitachse gespiegelt |
| Deutlich ist hier zu erkennen, dass verpolt nicht phasenverschoben sein kann |
| Es geht hier um die viel diskutierten Themen: "Phasenverschiebung vs. Invertierung eines Signals" und "Phasenverschiebung vs. Zeitverschiebung eines Signals". Der Begriff Phasenverschiebung ist angeblich nur für monofrequente Signale (Sinussignale) definiert und der Phasenverschiebungswinkel ist ausdrücklich nur für sinusförmige Größen definiert. |
Der typische Ø (phi)-Schalter ist schlicht ein Verpoler
Es wird absolut nichts "verschoben" auch keine Phase
| Merke: Zeit, Frequenz und Phase gehören dicht zusammen. Die Höhe der Amplitude hat keinen Einfluss auf diese Parameter. |
| Etwas anderes ist bei einem RC-Glied der 6 dB pro Oktave Gang, der die Amplitude bei der Grenzfrequenz um 3 dB dämpft. Die Phasenverschiebung ist an dieser Stelle immer 45°. R-C Filter und Grenzfrequenz: http://www.sengpielaudio.com/Rechner-RCglied.htm Frequenzgang und Entzerrung EQ: http://www.sengpielaudio.com/Rechner-zeitkonstante.htm Phase und Amplitude: Filter (RC-Glied) mit 6 dB pro Oktave: http://www.sengpielaudio.com/FilterMit6dBproOktave.pdf |
Die Kreisfrequenz ist ω = 2π · f
| Gegeben ist die Gleichung: y = 50 sin (5000 t) Bestimme die Frequenz und die Amplitude. Antwort: Die Amplitude ist 50 und ω = 5000. Die Frequenz ist f = 1/T = ω / 2 π = 795,77 Hz. |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
zurück  |
Suchmaschine  |
Startseite  |
