

| English version |
Die natürliche Einheit zum Messen von Winkeln ist das Bogenmaß, die man aus der Formel für den
Kreisumfang erhält: c = 2 · π · r, wobei r der Radius ist. Wenn r = 1, dann ist c = 2 · π. Somit ist
das Bogenmaß definiert, dass der Kreis 2 · π als Bogenmaß ist und das sind auch 360°.
1 Bogenmaß (radiant) = 360 / 2 · π = 57,295779513082320876798154814106 Grad
und 1 Grad = 0,017453292519943295769236907684886 Bogenmaß (radiant)
1 arcmin = 0,000290888208665722 Bogenmaß (radiant)
1 arcsec = 0,00000484813681109536 Bogenmaß (radiant)
Gradmaß (auch Altgrad oder Grad genannt) heißt DEG und Bogenmaß heißt RAD
Gon, früher Neugrad. Gon-System (rechter Winkel = 100 gon = 100g °
1 g = 100 Neuminuten º = 100 c; 1 c = 100 Neusekunden º = 100 cc = 1 GRD
Die Mehrzahl der Computerprogramme rechnen im Bogenmaß:
Pi = 4 · ARCTAN(1)
rad = grad · ARCTAN(1) / 45
grad = rad · 45 / ARCTAN(1)
Je nach Programm heißt es ARCTAN(1), arctan(1), ATN(1) oder atan(1).
Umrechnungsformeln (engl.)
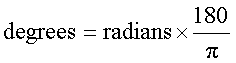
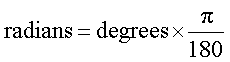
Umrechnung von Bogenmaß (RAD)nach Grad (DEG):
Winkelgrad = Winkelbogen · 180 / π ~ 57,296 · Winkelbogen
oder DEG = RAD · 180 / π ~ 57,296 · RAD
Umrechnung von Grad (DEG) nach Bogenmaß (RAD):
Winkelbogen = Winkelgrad · π / 180 ~ 0,01745 · Winkelgrad
oder RAD = DEG · π / 180 ~ 0,01745 · DEG
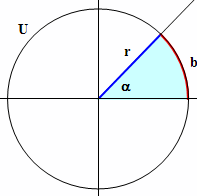
Unter dem Bogenmaß b eines Winkels α (im Gradmaß) verstehen wir die Länge
desjenigen Bogens b, der dem Winkel α im Einheitskreis (Radius r = 1) gegenüber liegt.
Zwischen Bogenmaß b und Gradmaß α besteht die lineare Beziehung:
b / α = 2 π / 360 = π / 180
| Winkel | Winkelgrad | Pi-Anteil | in Zahlen |
| 90° | π/2 | 1,570796327 | |
| 60° | π/3 | 1,047197551 | |
| 45° | π/4 | 0,785398163 | |
| 30° | π/6 | 0,523598775 |
| Winkelgrad | Bogenmaß |
| 0° | 0 |
| 45° | π/4 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
Winkel-Umrechnung
| zurück |
Suchmaschine |
Startseite |