

| English version |
| Eine stehende Welle ist der Schwingungszustand eines zusammenhängenden Systems. Als Musterbeispiel wird dafür üblicherweise die schwingende Saite eines Musikinstruments oder die Luftsäule in einer Orgelpfeife genommen. Diese Wellen haben zwar ein wellenartiges Aussehen, bewegen sich aber nirgendwohin; d. h. sie schwingen zeitlich aber nicht örtlich – sie sind ortsfest. Die Saite ist mit einer Länge L zwischen zwei festen Enden eingespannt, an denen sich immer ein Schwingungsknoten befindet. Zwischen diesen zwei Knoten (Nulldurchgang) ergibt sich ein Maximum, das auch Schwingungsbauch oder Wellenbauch genannt wird. Dargestellt sind hier die Eigenschwingungen einer idealisierten Saite, die als perfekt gleichmäßig und vollständig biegsam angenommen werden, d. h., sie setzen einer Biegung keinerlei Schwingungswiderstand entgegen. Es wird keinerlei Dämpfung durch innere Reibung angenommen, wobei die Steifigkeit Null ist. Die Frequenzen der Eigenschwingungen bilden eine harmonische Teiltonreihe. Diese Teiltöne werden auch Harmonische oder Partialtöne genannt. L = Länge der Saite, c = Schallgeschwindigkeit. Die 1. Harmonische ist die Grundwelle. |
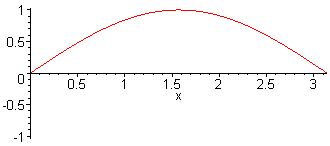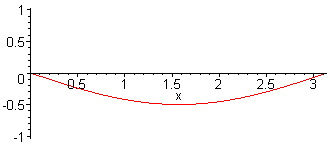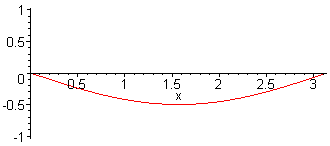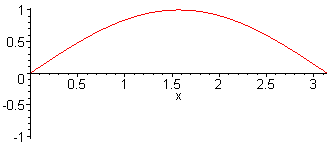 1. Harm. L = λ/2 = π f1 = c / (2·L) |
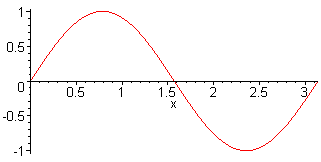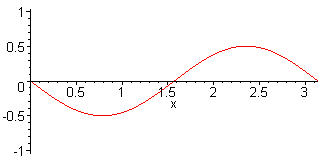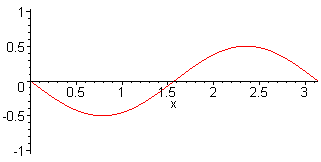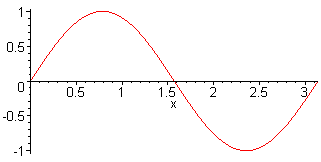 2. Harm. L = λ f2 = 2·f1 = c / L |
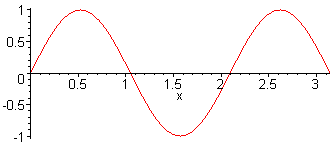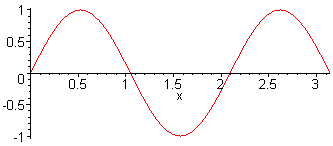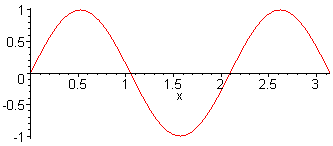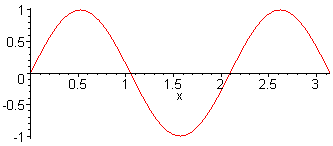 3. Harm. L = 3 λ / 2 f3 = 3·f1 = 3·c / (2·L) |
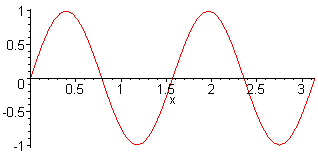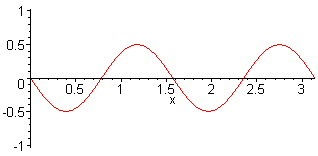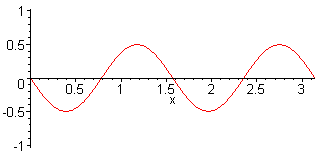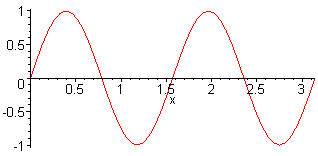 4. Harm. L = 2 λ f4 = 4·f1 = 4·c / (2·L) |
| Merke: Der Abstand zwischen zwei Knoten (nodes) oder zwei Bäuchen (antinodes) ist λ/2. Der Abstand zwischen einem Knoten (Nulldurchgang) und einem Bauch (Maximum) ist λ/4. |
| Zur Beachtung, denn es gibt häufig Verwirrung: Ein Bauch beim Schallwechseldruck (pressure antinode) ist zur gleichen Zeit (!) ein Knoten bei der Auslenkung der Luftteilchen (particle displacement node). Meistens wird vergessen, dem Betrachter der Abbildungen mitzuteilen, worum es sich handelt: um den Schallwechseldruck oder um die Bewegung der Auslenkung der Luftteilchen. Das ist ein Unterschied. |
2. Stehende Wellen (akustische Resonanz) bei Rohren (Flöten)
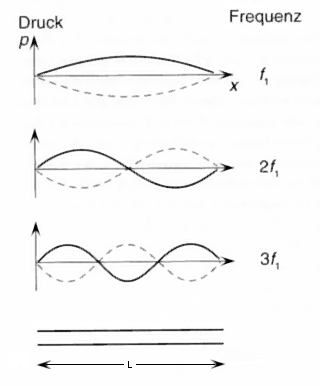 |
1. Harm. L = λ / 2 = π f1 = c / (2 · L) 2. Harm. L = λ f2 = 2 · f1 = c / L 3. Harm. L = 3 λ / 2 f3 = 3 · f1 = 3 c / (2 · L) Offenes Rohr |
| Eigenschwingungen einer Luftsäule in einem offenen Rohr (Röhre, Flöte). Am offenen Ende muss theoretisch jeweils ein Schalldruck-Knoten liegen, wenn man die Endkorrektur außer Acht lässt. Begründung: Am Rohrende wird die Druckwelle wegen des unendlichen Querschnittssprungs des Rohrs nahezu vollständig reflektiert (schallweicher Rohrabschluss und 180°-Phasendrehung der reflektierten Welle). Dabei ist der Schalldruck gleich Null (Druckknoten), weil die Impedanz am Rohrende gleich Null ist (kein Widerstand, aber Reflexion). |
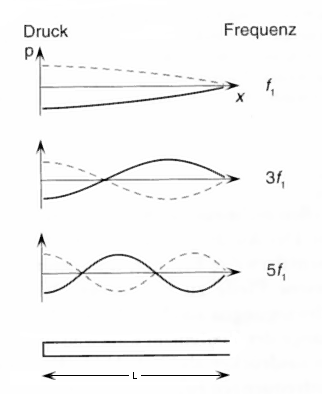 |
1. Harm. L = λ / 4 = π · 1 / 4 f1 = c / (4 · L) 3. Harm. L = 3 λ / 4 f3 = 3 · f1 = 3 c / (4 · L) 5. Harm. L = 5 λ / 4 f5 = 5 · f1 = 5 c / (4 · L) Links einseitig geschlossenes Rohr |
| Eigenschwingungen einer Luftsäule in einer einseitig geschlossenen Röhre (Flöte); auch gedackte Pfeife. Am geschlossenen Ende muss theoretisch jeweils ein Maximum (Schalldruckbauch) liegen. |
| Es gibt Missverständnisse bei Wellen in der Luft, weil sinusförmigen Signale die Knoten und die Bäuche der Schallauslenkung, der Partikelgeschwindigkeit des Schalls, vom Schalldruck oder von der Schalldichte sein können. Tontechniker mit Mikrofonen sind allein am Verhalten des Schallwechseldrucks in der Luft interessiert. Merke: Ein Knoten beim Schalldruck entspricht einem Bauch der Schallauslenkung! |
3. Raummoden (Stehende Wellen) bei schallharten parallelen Wänden
Wo stelle ich meine Lautsprecher hin? Wo ist der beste Abhörplatz? Wohin mit der akustischen Dämpfung?
Folgende Grundlagen zur Akustik der Schallwellen bei tiefen Frequenzen in Räumen sollte man dazu kennen.
Das gilt für den Aufnahmeraum genauso wie für den Wiedergaberaum = Regieraum oder das Wohnzimmer; siehe:
Raummoden und Saitenschwingungen
| Die Raumresonanzen, die sich zwischen den Begrenzungsflächen eines Raumes bilden, nennt man "stehende Wellen" oder Raumeigenmoden, auch kurz Moden. Sie entstehen, wenn ein Vielfaches der halben Wellenlänge (λ/2) zwischen die Begrenzungsflächen eines Raums passt. Voraussetzung für eine Raummode ist eine stehende Welle. Uns Tontechniker interessiert das Verhalten des Schalldrucks, weil durch seine Wirkung unsere Trommelfelle und die Mikrofonmembranen bewegt werden; siehe: Die Wirkung und die Ursache. Raummoden sind nichts anderes als stehende Wellen, die sich in jedem Raum bei tiefen Frequenzen ausbilden. Nicht-parallele Wände sind kein Mittel dagegen. |
 |
Eine stehende Welle als Schalldruckverteilung; hier:
3. Harmonische (2. Oberschwingung) − 3 Knoten und 4 Bäuche
Raummoden (Eigenschwingungen) als Schalldruckverteilung
Der Fachbegriff heißt eine Mode, also die Mode und der Plural sind mehrere Moden. Vergiss also Modus und Modi.
Berechnen der drei Moden (Raummoden) - Raumresonanzen von Rechteck-Räumen
| Merke: Praktisch sind Raummoden nur als tiefe Schalldruck-Frequenzen unterhalb von 300 Hz störend hörbar. Höhere modale Frequenzen verlieren an Bedeutung, denn ihre Störwirkung wird durch andere raumakustische Effekte überdeckt, weil die modale Dichte so hoch wird, dass keine selektive Modenhäufungen mehr auftreten, die sich als störende Klangfärbung bemerkbar machen. An harten Wänden bilden sich bei den Moden immer Schalldruckmaxima aus - das sind Wellenbäuche bzw. Schallauslenkungs-Minima. - "Lose Enden". |
| Mit folgender Formel lassen sich stehende Wellen, also Raumresonanzen (Moden), die zwischen den schallharten Begrenzungsflächen eines Rechteck-Raums (genauer: quaderförmig) entstehen, in ihrer Frequenz bestimmen. 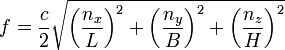 f = Frequenz der Mode in Hz c = Schallgeschwindigkeit 343 m/s bei 20 °C nx = Ordnungszahlen der Eigenschwingungen (Raumlänge) (1, 2, 3, ...) ny = Ordnungszahlen der Eigenschwingungen (Raumbreite) (1, 2, 3, ...) nz = Ordnungszahlen der Eigenschwingungen (Raumhöhe) (1, 2, 3, ...) L, B, H = Länge, Breite und Höhe des Raums in Meter An einer schallharten reflektierenden Wand (Grenzfläche) ist der Schallabsorptionsgrad α = 0 Eine stehende Welle 1. Ordnung mit der Grundschwingung = f1 entsteht, wenn die halbe Wellenlänge der Erregerschwingung genau in den Abstand der harten Begrenzungs- flächen passt. Für die axiale Mode gilt dabei als tiefste Frequenz: c = Schallgeschwindigkeit (343 m/s bei 20 °C) f1 = Grundfrequenz der axialen Mode in Hz L = maximaler Abstand der Begrenzungsflächen in Meter. Die stehenden Wellen höherer Ordnung berechnen sich aus den ganzzahligen Vielfachen der Mode 1. Ordnung. f3 = 3 · f1 f4 = 4 · f1 |
|
Bäuche Druckmaximum |
Knoten Nulldurchgang |
Wellenlänge | Frequenz | Harmonische | Oberschwingungen |
| 2 | 1 | λ = 2 · L | f1 = 1 · c / (2 · L) | 1. Harmonische | Grundschwingung | |
| 3 | 2 | λ = L | f1 = 2 · c / (2 · L) | 2. Harmonische | 1. Oberschwingung | |
| 4 | 3 | λ = (2 · L) / 3 | f1 = 3 · c / (2 · L) | 3. Harmonische | 2. Oberschwingung | |
| k + 1 | k | λ = (2 · L) / k | f1 = k · c / (2 · L) | k. Harmonische | (k − 1). Oberschwingung |
| k = 1, 2, 3, ... |
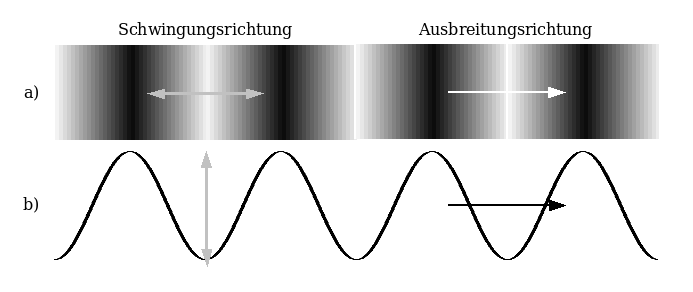
| Der Schallwechseldruck ist in Wirklichkeit eine Longitudinalwelle a), im Gegensatz zur hier besser darstellbaren Transversalwelle b). |
 |
| Stehende Welle als Schalldruckverteilung zwischen den Wänden. Eine Welle mit offenen Enden. |
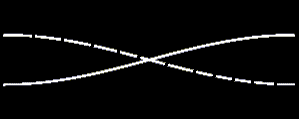 1. Harm. L = λ / 2 = π f1 = c / (2·L) |
 2. Harm. L = λ f2 = 2·f1 = c / L |
 3. Harm. L = 3 λ / 2 f3 = 3·f1 = 3·c / (2·L) |
 4. Harm. L = 2 λ f4 = 4·f1 = 4·c / (2·L) |
Hier wird der Schallwechseldruck einer Sinusschwingung und ihren Harmonischen |
| Das sind keine Darstellungen von Schalldruckschwingungen zwischen zwei Wänden in einem kleinen Raum ... ... sondern das sind Saiten- schwingungen (Amplituden). |
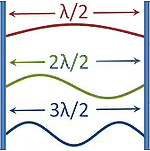 |
Eine typische Falschdarstellung mit Knoten an den Wänden. Die Darstellung der Schallauslenkung war nicht gewünscht. |
| Eine Saite ist zwischen zwei "festen Enden" eingespannt. An den Enden erscheint ein Wellenknoten. Eine Welle zwischen zwei harten Wänden wird beim Schalldruck mit "losen Enden" betrachtet. Daher erscheint als Schalldruck an den Wandseiten ein Wellenmaximum bzw. ein Wellenbauch. |
Siehe hierzu unrichtig: Stehende Welle - Wikipedia und Raummode - Wikipedia
Hier ist es richtig: From Wikibooks, the open-content textbooks collection
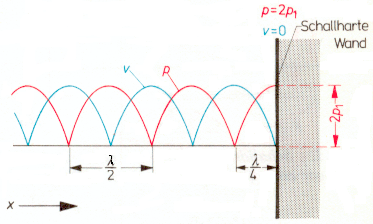 |
| Räumliche Verteilung vonSchalldruckbetrag p (rot) und Schallschnelle v (blau) bei einer stehenden Welle als totale Reflexion an einer schallharten Wand (schematisiert). Im Abstand von λ / 4 von der Wand ist der Schalldruck p = 0. Da die Absorptionswirkung in einem Material proportional zur Schallschnelle ansteigt, sollte sich der Absorber wirkungsvoll im Schnelle-Maximum d/4 als Wandabstand befinden oder sollte eine entsprechende Dicke haben. Viel einfacher als das Schnellemaximum ist das Schalldruck-Minimum messbar, das genau an der Stelle des Schnelle-Maximums bei λ/4 liegt. |
| Hier ist eine schöne Animation einer stehenden Welle - Erklärung durch Überlagerung der hinlaufenden mit der reflektierten Welle. Dazu muss man einstellen: "Reflexion am losen Ende". http://www.walter-fendt.de/ph14d/stwellerefl.htm |
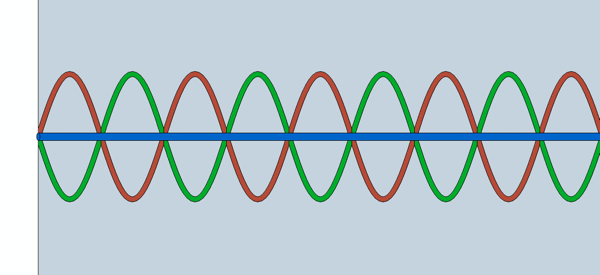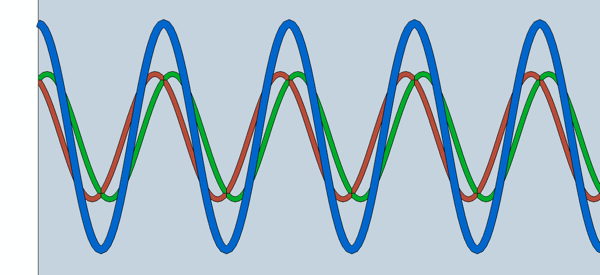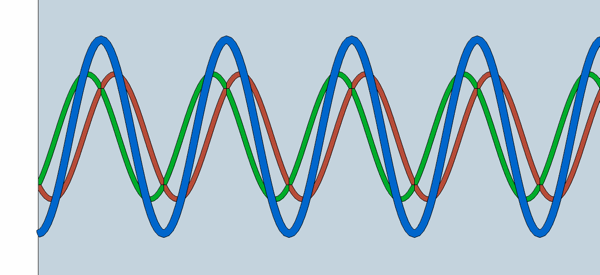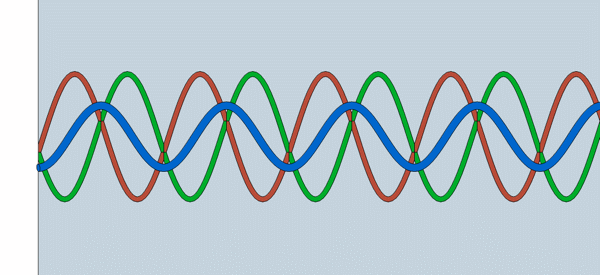 |
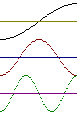
| Die rote Welle ist die einfallende Schallwelle, die grüne ist die zurückreflektierte Schallwelle. Die blaue ist die stehende Welle, die sich durch die Überlagerung beider Wellen ergibt. Voraussetzung für eine Raummode ist eine stehende Welle, jedoch sind stehende Wellen im Allgemeinen keine Raummoden. Diese beiden Begriffe werden üblicherweise nicht ganz korrekt als gleichbedeutend dargestellt. |
|
|
|
Zwei verschiedene Grenzflächenmikrofon-Bauarten
Untere Grenzfrequenz beim Grenzflächenmikrofon
Stehende Wellen auch bei offenen und gedackten Orgelpfeifen
| Gegenüberstellung der Reflexionen im Hallraum und einem extrem stark gedämpften Raum |
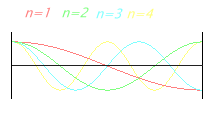 |
| Schalldruckreflexionen (Moden) an schallharten Wänden, wie in einem Hallraum. |
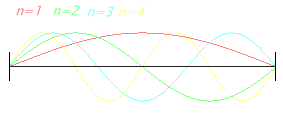 |
| Schalldruckreflexionen (Moden) an schallweichen Wänden, wie in einem reflexionsarmen Raum. |
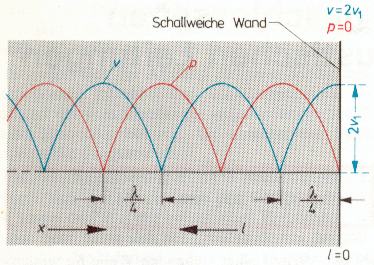 |
| Räumliche Verteilung von Schalldruck p (rot) und Schallschnelle v (blau) in einer stehenden Welle bei totaler Reflexion an einer schallweichen Wand (schematisiert). Im Abstand von λ / 4 von der Wand ist der Schalldruck p = max. |
|
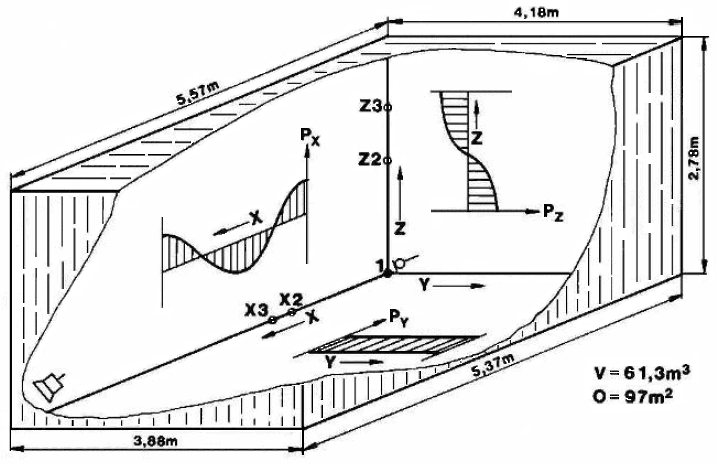
| Ein typischer Raum (Regieraum) mit Axial-Moden und Schalldruckbäuchen an den Wänden |
| Das Bild links zeigt dort die Schwingungen einer Saite mit außen liegenden Knoten. Das Bild rechts zeigt dort die tatsächliche Schalldruckverteilung an den Wänden. Dieses ist nur für 2D definiert, was üblicherweise genügt. Unter bestimmten Annahmen und Rundungen lassen sich ähnliche Aussagen jedoch auch für 3D treffen. |
Berechnen der drei Moden (Raummoden) - Raumresonanzen von Räumen
|
Der Druckkammer-Effekt
| Auch unterhalb der tiefstmöglichen Raummode sind tieffrequente Töne wiederzugeben. Man nutzt den Druckkammereffekt bei kleinen mit schallharten Begrenzungsflächen ausgestatteten Räumen, wobei der Raum druckdicht verschlossen sein muss. Siehe: Grundlagen der Raumakustik. Die "dB Drag Racing" Fans brauchen das für ihre Lautstärke-Wettbewerbe im Auto. |
 |
| RPG Triffusor |
| Absorption - Reflexion - Diffusität - Kombination |
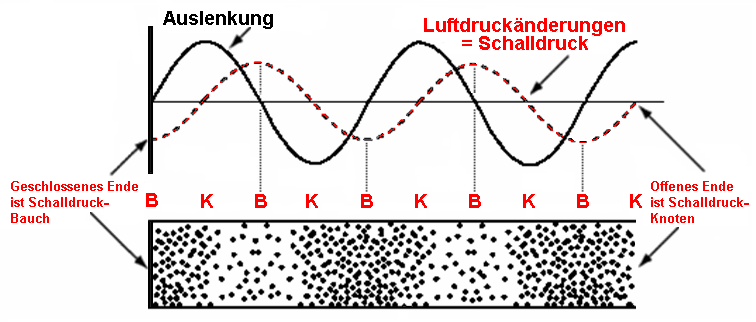 |
| Achtung: An einer harten Reflexionswand (closed end) gibt es einen Schalldruckbauch (pressure antinode) aber zur gleichen Zeit einen Auslenkungsknoten der Luftteilchen (particle displacement node). Wenn man von stehenden Wellen spricht, muss deutlich ausdrückt werden, dass wir Amplituden der Schalldruckveränderungen meinen, die auch unsere Trommelfelle bewegen. Meistens wird das vergessen. Der Schallwechseldruck in Luft schwingt mit Bauch und Knoten - gleichzeitig schwingt die Auslenkbewegung der Luftteilchen mit Knoten und Bauch. Die Beziehung zwischen dem maximalen Schallwechseldruck Δ pm und der maximalen Auslenkamplitude der Luftpartikel ξm is: Δ pm = (v ρ ω) ξm. |
| Unterscheide die Amplituden von Schallauslenkung der Luftteilchen, Schalldruck, Schallschnelle und Druckgradient. Schalldruckbauch (sound pressure antinode) ist Auslenkungsknoten der Bewegung der Luftteilchen (particle displacement node). Auslenkungsbauch der Luftteilchenbewegung ist Schalldruckknoten. |
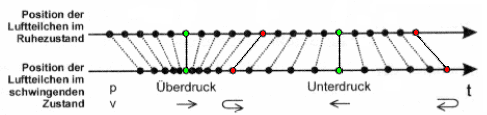 |
| Im Ruhezustand hat ein grünes Luftteilchen die gleiche Lage wie im schwingenden Zustand. Die Schallauslenkung der Luftteilchen befindet sich dabei im Nulldurchgang während die Schalldruckamplitude p dabei ein Maximum (Überdruck, Verdichtung) oder ein Minimum (Unterdruck, Verdünnung) zeigt. Im Ruhezustand ist ein rotes Luftteilchen im Maximum oder Minimum der Amplitude der Schallauslenkung und gleichzeitig ist das ein Nulldurchgang der Schalldruckschwingung. Somit ist dort der Schallwechseldruck Null; d. h. der normale statische Luftdruck ist allein vorhanden. |
| Vermeide das Wort "Ausschlag", was scherzhaft mit "Schall-Akne" bezeichnet wird. Auslenkung der Luftteilchen klingt besser. |
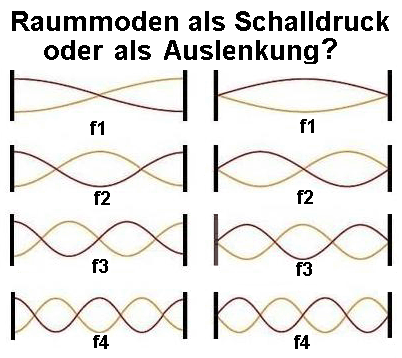 |
| In bildlichen Darstellungen von stehenden Wellen (Raummoden) zwischen zwei Wänden wird selten angegeben, ob der Schalldruck als Druckschwankung in der Luft oder die Auslenkung der Luftpartikel dargestellt sein soll. Diese Klärung ist jedoch unbedingt notwendig. Bei obiger Abbildung erkennt man den wichtigen Unterschied. Links = Schalldruck (Bauch) entspricht rechts = Auslenkung (Knoten). Zum Nachdenken: Die Auswirkung stehender Wellen meldet uns unser Gehör, und der Schalldruck bewegt wirkungsvoll unsere Trommelfelle. |
| zurück |
Suchmaschine |
Startseite |