

| English version |
| Die subjektiv empfundene Lautstärke und der künstliche Begriff Lautheit
sind Begriffe, welche versuchen die Wahrnehmungsstärke des Schalls
durch unser Gehör beschreiben. Die Bestimmung der Lautheit von station ren Signalen ist in der Norm ISO 532 bzw. DIN 45631 festgelegt. |
| Die Lautheit eines Geräuschs wird in Sone angegeben. Der Lautstärkepegel eines Geräuschs wird in Phon angegeben. |
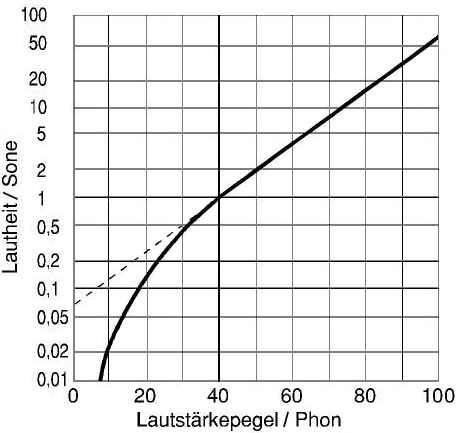
| Der Lautheit N = 1 Sone entspricht40 Phon, das ist der Lautstärkepegel
LN = 40 dB bei einem Sinuston mit der Frequenz von f = 1000 Hz. Kurt Tucholsky schrieb treffend: "Der eigene Hund macht keinen Lärm - er bellt nur." "Es gibt viele Arten von Lärm - aber nur eine Stille" und "Lärm ist das Geräusch der anderen". Lautheit ist eine persönliche subjektiv empfundene Eigenschaft des Schalls - im Gegensatz zum Schalldruckpegel SPL in Dezibel, der dagegen objektiv und direkt messbar ist. |
Umrechnung gültig zwischen 40 phon und 120 phon
Das heißt für größere Werte als '1 sone entsprechend 40 phon'
Für Lautstärkepegel LN > 40 phon: Lautheit N in sone = 2[(LN − 40)/10] (LN in phon)
Für Lautheit N > 1 sone: Lautstärkepegel LN in phon = 40 + [10 · log N / log102] (N in sone)
log 2 = 0,30103 LN in phon = 40 + 33,22 · log N (N in sone)
Umrechnung gültig nur zwischen 8 phon und 40 phon
Das heißt für kleinere Werte als '1 sone entsprechend 40 phon'
Für Lautstärkepegel LN < 40 phon: Lautheit N in sone = (LN / 40)2,86 − 0,005
(LN in phon)
Für Lautheit N < 1 sone: Lautstärkepegel LN in phon = 40 × (N + 0,0005)0,35 (N in sone)
| Nach der Definition von Stanley Smith Stevens entspricht 1 Sone genau 40 phon. Das ist der Lautstärkepegel eines 1-kHz-Sinustons mit LN = 40 dB-SPL oder dBA, aber nur (!) für einen Sinuston von 1 kHz und nicht für Breitbandgeräusche. Es gibt keine "dBA"-Kurve für die frequenzabhängige Hörschwelle beim menschlichen Hören. "dBA" hat absolut nichts mit Sone, mit Phon oder mit dem Schalldruckpegel in dB zu tun. 60 phon bedeutet: "so laut, wie ein 1000 Hz Sinuston mit einem Pegel von 60 dB." |
Zusammenhang zwischen Lautheit N in sone
und Lautstärkepegel LN in phon
 |
|
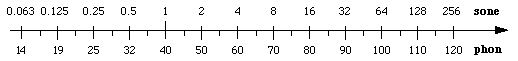 |
| Lautheit N (sone) und Lautstärkepegel LN (phon) k nnen - wie
hier gezeigt wird - problemlos ineinander umgerechnet werden. Der psychoakustisch empfundene Lautstärkepegel und der objektiv gemessene Schalldruckpegel dBSPL ist jedoch nicht in den bewerteten dBA-Pegel umzurechnen. Die häufige Frage: "Wie ist eigentlich die Umrechnung von Sone in dB?" oder "Was ist denn 0,5 sone in Dezibel (dB) als Schalldruckpegel (SPL) umgerechnet?" kann wirklich nicht beantwortet werden. Nur ein einzelner Sinusston von 1 kHz gemessen in Phon ist der Angabe in dB-SPL gleichzusetzen. Sorgfältig sind bei der Lautstärke auseinanderzuhalten: Sone gehört zur Lautheit. Phon gehört zum Lautstärkepegel. Vermeide hierbei das laienhafte Wort "Intensität". dB oder dB-SPL gehört zum Schalldruckpegel. dBA ist ein Filter für grob vereinfachte Bewertung der Lautstärke. |
| Die Lautstärke eines Geräuschs wird rein subjektiv empfunden. Um die
Lautstärke zu "messen", wird die Lautstärke eines 1000 Hertz-Sinustons so laut
eingestellt, bis es von Hörern ebenso laut wie das Geräusch empfunden wird. Der
Lautstärkepegel des Schalls in Phon ist dann gleich dem Schalldruckpegel in dB. Der Pegelwert eines bewerteten oder eines unbewerteten 1 kHz-Sinustons sollte identisch sein. Die Lautheit gibt an, wie laut Schall rein subjektiv empfunden wird. Sie ist also eine psychoakustische Empfindungsgröße mit großer Toleranz und keine wirkliche Messgröße. Es gibt keine Umrechnungsformel. Die persönlichen subjektiven Empfindungen der Lautst rke und der Lautheit beim Lärmempfinden entziehen sich als psychoakustische Werte einfacher physikalischer Messung. Merke: "Lautheit ist ein künstlicher Begriff (engl. loudness) aus der Psychoakustik, dem in der Umgangssprache die Lautstärke entspricht". Der Begriff Lautheit wurde erst 1936 von Stanley Smith Stevens mit dem Fachbegriff "Sone" und loudness als "Lautheit" von den Psychoakustikern bei uns eingeführt. |
| Der normale Mensch kennt nur Lautstärke und hat ein etwas komisches Gefühl bei dem Wort Lautheit. |
| Dieser nicht auszuhaltende Satz musste unter dem Begriff "Lautheit" von einem
"ordentlichen" Administrator aus Wikipedia beseitigt werden. Darum steht dieser unerwünschte, also störende Satz jetzt unlöschbar hier. DIN 45631 und ISO 532 B beschreiben jedoch genormte "Messverfahren" zur "Lautheitsmessung". Diese Messverfahren "bestimmen" wahlweise den Lautstärkepegel in phon oder die Lautheit in sone. Da die unmittelbare "Bestimmung" der psychoakustischen Lautheit jedoch recht schwierig ist, wurde zwischen der Lautheit N in sone und dem Lautst rkepegel LN in phon folgende Beziehung festgelegt (ISO-Empfehlung ISO/R 131-1959): Lautheit N = 2(LN - 40)/10 oder Lautst rkepegel LN = 40 + 10 · lb N. "lb" bezeichnet den Logarithmus zur Basis 2. 10 · lb N = 10 · log2(N) |
| Sone ist die Maßeinheit der subjektiven Lautheit eines Klangs nach dem
Vorschlag von Stanley Smith Stevens (1906-1973) aus dem Jahre 1936. Ein
Lautstärkepegel von 40 phon soll dabei 1 sone sein und das entspricht der
Lautstärke eines Sinustons mit der Frequenz 1 kHz und einem Schalldruckpegel
von 40 dBSPL. Somit hat ein "doppelt so laut" empfundener Schall dann eine
Lautheit von 2 sone und ein "vierfach so laut" empfundener Schall die Lautheit 4
sone. Frage: Wie empfindet man wirklich, wann etwas genau doppelt so laut
ist? Diese Frage wird allgemein nicht gestellt. Punkt. Es ist eben einfach so. Um ganz genau zu sein, müssen Messungen in Sone durch die zusätzliche Nachsilbe G gekennzeichnet sein, was bedeutet, dass der Lautstärkewert aus Frequenzgruppen errechnet wurde und einer der beiden Nachsilben zusätzlich F (f r Freifeld) oder D (für Diffusfeld) angibt. Dieses ist jedoch recht selten der Fall. Im Allgemeinen werden Geräusche von unter einem sone als recht leise empfunden. In Umgebungen mit Hintergrundgeräuschen (PCs, Klimaanlage oder Ähnliches) mögen bis zu zwei sone noch hingenommen werden. Alles darüber lässt sich kaum ignorieren. Werte über drei sone gelten schon als laut. Lautheits-Tabelle: 0,3 sone: Blätterrascheln (ca. 26 dB) 1 sone: Rauschen von Klimaanlagen (ca. 40 dB) 2 sone: Normale Unterhaltung in 1 m Entfernung (ca. 50 dB) 4 sone: Fernseher auf 'Zimmerlautstärke' *) (ca. 60 dB) 8 sone: Alte Schreibmaschine in 1 m Entfernung (ca. 70 dB) *) Es gibt keine objektive Definition der Zimmerlautst rke anhand von Schallpegelwerten; siehe: http://de.wikipedia.org/wiki/Zimmerlautstärke Es gibt noch weitere Größen, die sich mehr mit der Lästigkeit, d. h. mit der psychologischen Auffälligkeit beschäftigen. Die Einheiten dafür sind acum als psychoakustische Schärfe eines Hörereignisses, asper als psychakustische Rauhigkeit und vacil als subjektiv empfundene Schwankungsstärke. Hersteller geben die "Lautstärke" ihrer Geräte oft in sone oder auch in dBA an, als Dezibel, gemessen mit der A-Bewertung. Sone und dBA lassen sich nur bei einer konstanten Frequenz ineinander umrechnen. Bei der Sone-Skala soll einer Verdopplung des Sone-Werts ungefähr einer subjektiv wahrgenommenen Verdopplung der Lautstärke entsprechen und bei der Dezibel-Skala soll etwa ein um 10 dBA höherer Wert einer empfundenen Verdopplung der Lautstärke entsprechen - versuchen uns die Psychoakustiker zu erklären. Die Lautheitsskala in sone beruht darauf, dass 1 sone halb so laut ist wie 2 sone und 9 sone dreimal so laut ist wie 3 sone. Diese subjektive Skala bildet das H rempfinden linear ab. Anmerkung: "Stell' doch mal das Radio auf doppelt so laut oder auch halb so laut." Wer dieses nicht ganz selbstsicher kann - der ist ganz normal. Lass' doch mal eine heiße Tasse Kaffee auf "halb so heiß" abkühlen - und denke dabei allgemein über die "Empfindung" halb laut oder doppelt so laut nach. Was ist das eigentlich genau? |
| Merke: Vergleich dB und dBA: Es gibt keine Umrechnungsformel von
gemessenen dBA-Werten in Schalldruckpegel dBSPL oder umgekehrt. Es gibt keine Korrelation zwischen dem Schalldruckpegel in dB-SPL als breitbandige Messung und der bewerteten Messung in dBA. |
| Ein fester Bezug besteht nur bei frequenzreinen Signalen, z. B. bei 1 kHz. Jedoch könnte man anhand dieser Tabelle die psychoakustischen Werte ungefähr "ganz vorsichtig" vergleichen. Die Amplitudenzusammensetzung des Signals ist meistens unbekannt. Der Abstand des Messpunkts hat eine ausschlaggebende Bedeutung für die Größe des gemessenen Werts. Man darf von dB-A-Messungen keine zutreffende Beschreibung der "Lautstärke" erwarten. |
| Eine typische Frage: Was ist dbA im Vergleich zu sone? Folgende Tabelle ist jedoch für die dBA-Werte kein genaues Wissen − sondern eher wildes Raten! Die "Umrechnung" von "sone in dBA" |
Umrechnung zwischen Sone und Phon −
jedoch nur ein recht grobes "Schätzen" derdBA-Werte
| sone | phon | dBA | sone | phon | dBA | |
| 0,1 | 17,9 | 20,5 | 1,8 | 48,5 | 34,8 | |
| 0,2 | 22,8 | 21,5 | 1,9 | 49,3 | 35,3 | |
| 0,3 | 26,2 | 22,5 | 2,0 | 50,0 | 35,8 | |
| 0,4 | 29,0 | 23,5 | 2,1 | 50,7 | 36,4 | |
| 0,5 | 31,4 | 24,4 | 2,2 | 51,4 | 37,0 | |
| 0,6 | 33,5 | 25,3 | 2,3 | 52,0 | 37,5 | |
| 0,7 | 35,3 | 26,3 | 2,4 | 52,6 | 38,0 | |
| 0,8 | 37,0 | 27,2 | 2,5 | 53,2 | 38,4 | |
| 0,9 | 38,6 | 28,2 | 2,6 | 53,8 | 38,8 | |
| 1,0 | 40,0 | 29,2 | 2,7 | 54,3 | 39,3 | |
| 1,1 | 41,4 | 30,2 | 2,8 | 54,9 | 39,8 | |
| 1,2 | 42,6 | 31,1 | 2,9 | 55,4 | 40,2 | |
| 1,3 | 43,8 | 32,0 | 3,0 | 55,9 | 40,6 | |
| 1,4 | 44,9 | 32,9 | 3,1 | 56,3 | 41,1 | |
| 1,5 | 45,9 | 33,5 | 3,2 | 56,8 | 41,5 | |
| 1,6 | 46,9 | 33,9 | 3,3 | 57,2 | 42,0 | |
| 1,7 | 47,7 | 34,4 | 3,4 | 57,7 | 42,5 |
| Audiogeräte zeigen in ihren Datenblättern häufig A-bewertete Pegel − nicht weil das mit unserem Gehör übereinstimmen würde − sondern weil damit beispielsweise Brummkomponenten versteckt werden können, die sonst ein Datenblatt schlechter aussehen lassen. Worte an helle Köpfe: Immer fragen, was ein Hersteller wohl zu verbergen hat, wenn die A-Frequenzbewertung angegeben wird. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
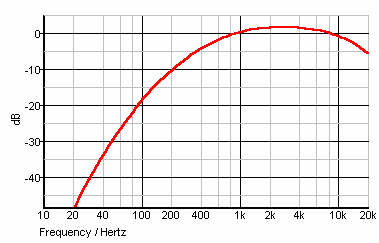 |
| Diese Frequenzbewertung mit der A-Kurve wird bei der Messung von Geräuschen
verwendet. Hierbei werden die Messgrößen durch ein Bewertungsfilter gewichtet,
das eigentlich den Frequenzgang des menschlichen Gehörs für leise Pegel unter
40 dB berücksichtigen soll. Dieses Filter wird jedoch gern für höhere Pegel
verwendet, ein Zweck für den es nie gedacht war und für den es sich nicht eignet. Daher liefert das A-Filter niedrigere Messwerte als unsere Ohren empfinden. Die abgeschnittenen tiefen Frequenzen werden demnach nicht gemessen. |
| Eine grobe Formel, mit dem Versuch sone ungefähr in dBA "umzurechnen": dBA = 33,22 · log (sone) + 28 mit einer Genauigkeit von vielleicht ±2 dBA oder Sone = 10^[(dBA − 28) / 33,22] |
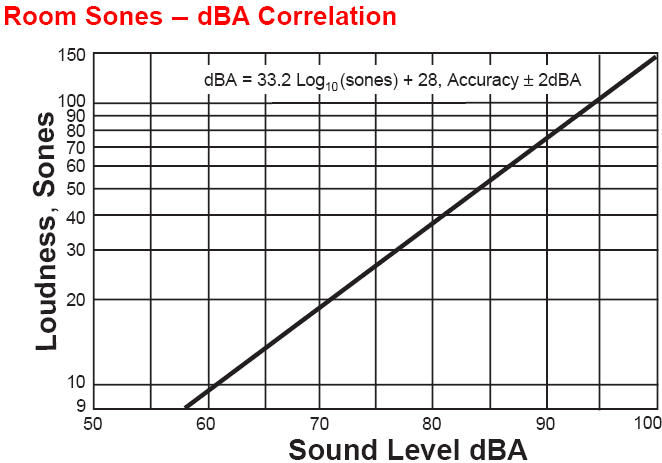
Merke: Der Dynamikumfang wird in den letzten Jahren immer häufiger allein A-bewertet angegeben,
auch wenn das für die Bewertung der Rauscharmut nicht sinnvoll ist. Das Marketing hat halt das Sagen.
Bewertungsfilter nach DIN EN 61672-1 2003-10 (DIN-IEC 651) −dBA und dBC
|
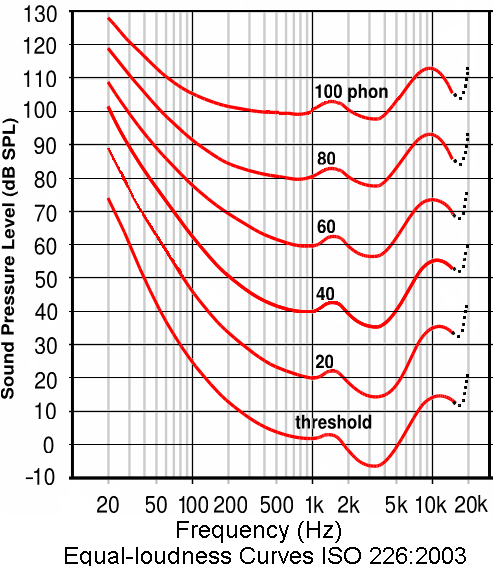
Phon ist eine Maßeinheit der psychoakustischen Größe für den
Lautstärkepegel. Neben der Lautheit in sone wird der Lautstärkepegel in
phon dazu benutzt, die empfundene Lautstärke, mit der ein Mensch ein
Schallereignis wahrnimmt, zu beschreiben. |
| Lautstärkepegel (LN in Phon): Subjektive (psychoakustische)
Lautstärkeempfindung Kurven gleicher Lautstärkepegel (Isophonen oder
Phonkurven) (Fletcher und Munson 1933, ursprünglich): Bezugston: 1000 Hz: Hier Schallpegel = Lautstärkepegel (dB = phon). Mit diesem werden andere Tonhöhen verglichen. Es zeigte sich: um subjektiv die gleiche Lautstärke zu erhalten, muss (besonders bei tieferen Frequenzen) der Schallpegel erhöht werden. Nach einer systematischen Durchmessung erhielt man im Hörfeld die "Kurven gleicher Lautstärke" (unter 80 dB der Hörschwelle nachempfunden, dar ber immer geradliniger werdend), auf denen die Frequenzen die gleiche Lautstärke wie der Bezugston bei 1000 Hz aufweisen, aber jedoch unterschiedliche Schallpegel. Lautheit (N in sone) (Stevens 1955): Empfindungsmäßige psychoakustische Aussage ber das Verhältnis zweier verschiedener Lautstärken zueinander: Kurven gleicher Lautheit: Bezugston: 1000 Hz bei 40 dB = 40 phon = 1 sone. Mit diesem werden andere Lautstärken verglichen. Wann ist etwas doppelt so laut/halb so laut? Oberhalb von 40 dB soll eine Verdopplung der Lautstärke bei einem Zuwachs von etwa 10 phon wahrgenommen werden, sagen uns die Psychoakustiker. Verhältnis zwischen Lautstärkezuwachs (phon, unten) und Lautheitsbewertung (sone, oben):
|
| Zum Nachdenken: Wenn wir eine Temperatur von 15 Grad Celsius
empfinden, halten wir die Frage, wie hoch denn empfindungsmäßig die
"doppelte Temperatur" davon sei, für blöd. Wenn wir den Schallpegel von 80 dB empfinden, scheint die Frage, wie hoch denn die "doppelte Lautstärke" davon sei, widerspruchslos hingenommen zu werden. Oder? |
|
Frage: "Wenn wir heute 15 Grad haben, wie warm müsste es morgen sein, wenn es doppelt so warm wäre?" Antwort: 0 Grad Celsius ist 273 Grad vom absoluten Nullpunkt entfernt. Das heißt −273 Grad Celsius entspricht Null. Somit haben wir heute 273 + 15 = 288 Grad. Das Doppelte davon ist 576 Grad vom absoluten Nullpunkt aus gerechnet für die Temperatur von morgen; wobei auf der Celsius Skala damit 576 − 273 = 303 Grad Celsius gemeint ist. Das ist unerträglich heiß! |
| Schallquelle ab (1/r²). Das ist ein häufig erzähltes und gern geglaubtes Märchen. |
|
Falsche Abnahme vom Schalldruck mit der Entfernung von der Schallquelle Newsgroups: Falsche Abnahme vom Schalldruck mit der Entfernung zur Schallquelle − ohne Quadrat! p ≈ 1 / r |
| Im Computerbereich sind zwei verschiedene Einheiten zur Einstufung des Ger uschs z. B. bei Lüfter und Festplatte gebr uchlich: Die Dezibel-Skala (Lautstärkepegel), und die Sone-Skala (Lautheit). Die Dezibel-Skala oder die Phon-Skala wird jedoch immer häufiger in der 'A'-gewichteten Form (dBA) angegeben; sie hat eine logarithmische Skala. Trotz einer Gewichtung, die dem menschlichen Hörvermögen entlehnt ist, sagt die dB(A)-Skala nur etwas ber den bewerteten (gefilterten) Schalldruckpegel bzw. die Lautheit eines Geräuschs aus, jedoch nichts über seine wirklich empfundene subjektive Lästigkeit. Genau dieses, sehr 'menschliche' Kriterium ist jedoch bei relativ leisen Störgeräuschen entscheidend. Als Beispiel sei der subjektive Vergleich zwischen dem Sirren einer Mücke und dem Murmeln eines Baches genannt: Obwohl letzterer mit einem weit höheren dB(A)-Wert gemessen würde, wird jeder das Mückenschwirren als viel störender einstufen. Daher ist recht schwierig, Aussagen ber die menschliche Empfindung der "Leisigkeit" bei Computern mit ihren Lüfter- und Festplattengeräuschen zu machen. Kaum sinnvoller sind die Messwerte mit der Sone-Skala, die auch keine anderen Faktoren ber cksichtigen, die f r das menschliche H rempfinden eine Rolle spielen. Bei Sone gilt: doppelter Zahlenwert = doppelt (?) so laut und ist damit doppelt so lästig (?). Was immer das auch sein soll. Zur Auswahl von Laptops und Computern, k nnen die Werte der folgenden Tabelle als Orientierung gelten, wobei darauf zu achten ist, dass nur solche Messwerte vergleichbar sind, die unter den gleichen Bedingungen ermittelt wurden. Der stärkste Einflussfaktor ist der Mikrofonabstand zur Schallquelle. Wenn nicht klar ist, ob bei zwei Messungen dieser Abstand gleich war, ist ein Vergleich der Werte sinnlos.
Im Zweifel sollte man nie auf ein Probeh ren verzichten. Es gibt kein preiswertes Messverfahren, das dem subjektiven Empfinden des Menschen einigermaßen entspricht. Die Behauptung, dass die Sone-Messung mehr "menschliche Daten" zur Ziemliche "Ungenauigkeit" auf: http://www.code-knacker.de/sone.htm "Im Unterschied zu anderen Messmethoden, wie etwa beim dB (Dezibel), Diese Antwort ist nicht richtig. Die Phon-Messung (Lautstärkepegel) hat gegenüber der Das physiologische Empfinden wird bei Sonemessungen eben nicht "Lautheit: Einheit Sone − Da die meisten menschenbestimmte Antwort: Die Phon- bzw. die dB-Messung bei einem Sinuston von 1 kHz hat gegenüber Behauptung: "Die Sone-Skala entspricht eher dem menschlichen Hören; Antwort: Dass 4 sone die meisten Menschen angeblich als doppelt so laut empfinden, wie |
Schallpegel-Vergleichstabelle mit Faktor
| Die Schallpegelabhängigkeit und die dazugehörende Änderung des Faktors bei subjektiver Lautstärke (Lautheit) und objektivem Schalldruck (Spannung) und Schallintensität (Leistung) Wieviel Dezibel (dB) Pegeländerung ist zweimal, halb oder gar viermal so laut? Wieviel dB erscheinen doppelt so laut zu sein? Hier sind die unterschiedlichen Faktoren. Faktor bedeutet "das Wievielfache", also "wie oft" ... Verdopplung der Lautstärke. |
| Pegel- Änderung |
Lautstärke Lautheit |
Spannung Schalldruck |
Schallleistung Schallintensität |
| +60 dB | 64 | 1000 | 1000000 |
| +50 dB | 32 | 316 | 100000 |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31,6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2,0 = Verdopplung | 3,16 = √10 | 10 |
| +6 dB | 1,52 fach | 2,0 = Verdopplung | 4,0 |
| +3 dB | 1,23 fach | 1,414 fach = √2 | 2,0 = Verdopplung |
| - - - - ±0 dB - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - |
| −3 dB | 0,816 fach | 0,707 fach | 0,5 = Halbierung |
| −6 dB | 0,660 fach | 0,5 = Halbierung | 0,25 |
| −10 dB | 0,5 = Halbierung | 0,316 | 0,1 |
| −20 dB | 0,25 | 0,100 | 0,01 |
| −30 dB | 0,125 | 0,0316 | 0,001 |
| −40 dB | 0,0625 | 0,0100 | 0,0001 |
| −50 dB | 0.0312 | 0,0032 | 0,00001 |
| −60 dB | 0.0156 | 0,001 | 0,000001 |
| Log. Größe | Psychogröße | Feldgröße | Energiegröße |
| dB- Änderung |
Lautstärke- faktor |
Amplituden- faktor |
Leistungs- faktor |
| Merke: Für eine 10 dB Pegeländerung brauchen wir zehnmal mehr Leistung vom Verstärker. Diese Erh hung des Schallpegels bedeutet eine Erhöhung des Schalldrucks um den Faktor 3,16. Die psycho-akustische Lautstärke bzw. Lautheit ist eine subjektive Empfindungsgröße. |
| Merke: Eine Anhebung des Schallpegels um 6 dB entspricht der Verdopplung des Schalldrucks. Eine Erhöhung des Schallpegels um 3 dB entspricht der Verdopplung der Schallintensität. Eine Anhebung des Schallpegels um 6 dB entspricht der Vervierfachung der Schallintensität. Eine Erhöhung des Lautstärkepegels um 10 dB soll der Empfindung doppelter Lautstärke entsprechen. Die subjektiv empfundene "Lautstärke" bzw. der "Lautstärkepegel" und der künstliche Begriff "Lautheit" ist als Empfindungsgröße des menschlichen Hörempfindens nicht mit der objektiven Messgröße Schalldruck in einen Topf zu werfen. Der Schalldruck als Schallfeldgröße ist nicht das Gleiche, wie die Schallintensität als Schallenergiegröße. |
Ist 10 dB oder 6 dB Schallpegeländerung eine Verdopplung oder Halbierung der Lautstärke? |
| Eine empfundene Verdopplung der Lautstärke entspricht etwa einer Pegeländerung zwischen 6 dB und 10 dB. |
| Es gibt eine ständige Unsicherheit bei der Antwort der Frage: "Wieviel dB ist denn eine Schallverdopplung"? oder "Was ist der doppelte Schall?" Antwort: Verdopplung heißt "Faktor 2". Was soll denn beim "Schall" doppelt sein? Die doppelte (Schall)-Intensität ergibt sich bei einer Schallintensitäts-Pegelerhöhung von 3 dB. Der doppelte Schalldruck ergibt sich bei einer Schalldruck-Pegelerhöhung von 6 dB ● Die doppelte Lautstärkeempfindung ergibt sich bei einer Lautstärke-Pegelerhöhung von etwa 10 dB. Doppelte Leistung = Faktor 2 ist 3 dB mehr berechneter Leistungspegel (Schallintensitätspegel). Doppelte Spannung = Faktor 2 ist 6 dB mehrgemessener Spannungspegel (Schalldruckpegel) ● Doppelte Lautheit = Faktor 2 ist 10 dB mehr empfundener Lautheitspegel (Psychoakustik). |
| Wie kann man Schallgrößen in Pegel umrechnen? Wieviel dB ist denn zweimal (doppelt, halb) oder dreimal so lauter Schall? Wie nimmt eigentlich der Schall mit der Entfernung ab? |
Kurven gleicher Lautstärke-Pegel ISO 226 − Die neue Norm
Akustik - Normalkurven gleicher Lautst rkepegel (ISO 226:2003)
| zurück |
Suchmaschine |
Startseite |