

| English version |
| Inkohärent bedeutet, dass die Signale der beiden Kanäle keinen Bezug zueinander haben. Auch der Begriff "unkorreliert" wird
hierbei verwendet. Inkohärente Signale sind immer unkorreliert und korrelierte sind immer kohärent. Umgekehrt trifft dieses nicht allgemein zu. Hier wirken mehrere Quellen als Überlagerung des Schalls zusammen. Unter Superposition versteht man generell eine Überlagerung: von lateinisch: super = über; positio = Lage, Setzung, Stellung. Sind zwei inkohärente Quellen gegeben, dann ist ihre kombinierte Wirkung die Summe ihrer akustischen Leistung. |
| Fülle so viele Pegel-Felder wie notwendig aus und klicke auf die Berechnungs-Taste,
um die berechnete Summe zu erhalten. Vorausgesetzt wird, dass jede Schallquelle zur
anderen eine Zufallsphasenlage hat. |
Addieren von bis zu dreißig (30) Pegeln in Dezibel
Umrechnung von Schalldruckpegel in Schalldruck und Schall-Intensität
Addition von Amplituden und Pegeln (kohärent und inkohärent)
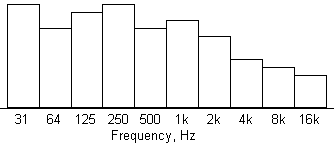
Die zehn Oktavbänder in unserem Hörbereich
Für den Summenschalldruckpegel von n inkohärent abstrahlenden Quellen gilt
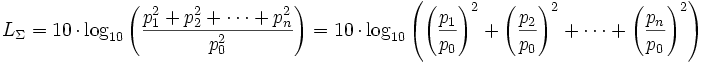
Der Bezugsschalldruck p0 ist 20 µPa = 0,00002 Pa = 2 × 10−5 Pa (Effektivwert) ≡ 0 dB.
Aus der Berechnungsformel des Schalldruckpegels ergibt sich unmittelbar, so dass gilt
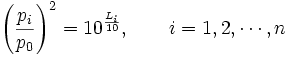
Dieses in die Gleichung zur Berechnung des Summenschallpegels eingesetzt, ergibt die gesuchte Additionsformel
![]()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3,01 | 2,54 | 2,12 | 1,76 | 1,46 | 1,19 | 0,97 | 0,79 | 0,64 | 0,51 | 0,41 |
 |
Addieren von gleich starken inkohärenten Schallsignalen
 |
|
||||||||||||||||||||||||||||||
| Mehrere gleich starke Schallquellen erzeugen an einem bestimmten Ort einen Schalldruck, bzw. einen Schalldruckpegel. Bei der Addition solcher inkohärenter Quellen vereinfacht sich die Gleichung zur Berechnung des Summenschalldruckpegels wie folgt: |
Formeln: Δ L = 10 × log n oder n = 10(ΔL/10)
Δ L = Pegelzunahme; n = Anzahl der gleich lauten Schallquellen.
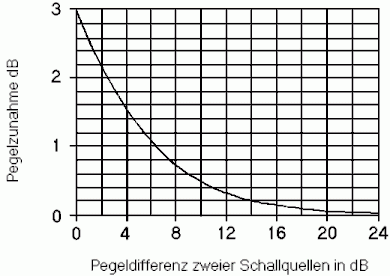
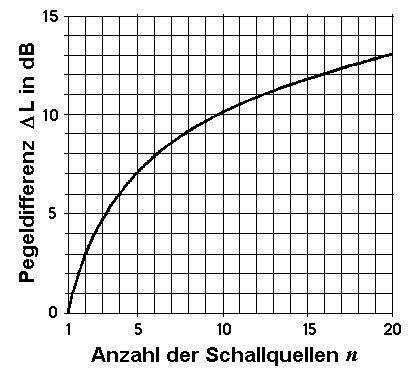
| Für n = 2 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 2 = +3,01 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 3 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 3 = +4,77 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. Für n = 4 gleich starke, inkohärente Schallquellen ergibt sich eine Pegelzunahme von 10 · log10 4 = +6,02 dB gegenüber dem Fall, dass nur eine Quelle vorhanden ist. |
![]()
Pegelzunahme bei gleichstarken inkohärenten Schallquellen
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beiden Richtungen des ↔ Zeichens. |
Der Gesamtpegel in dB ergibt sich aus dem Pegel einer Schallquelle,
zu dem die Pegelzunahme (der Pegelzuwachs) linear addiert wird.
| Beispiel: Der messbare Schallpegel eines Motorrads beträgt in einem
bestimmten Abstand 60 dB(A). Wie groß ist der Summenpegel bei 4
Motorrädern gleicher Lautstärke? Lösung: 60 dB(A) + 10 log 4 = 60 + 6 = 66 dB(A). Bei der Lärm-Messung von Motorrädern sollte zumindest über die "Ehrlichkeit" des dBA-Messwerts ohne tiefe Frequenzen nachgedacht werden. |
| Kohärente und inkohärente Schallpegel- und Schalldruckwerte sind problemlos zu addieren. Oft wird jedoch gewünscht, die psychoakustisch empfundenen Lautstärken oder Lautheiten zu addieren. Siehe: |
| Wieviel Dezibel (dB) Pegeländerung ist zweimal, halb oder gar viermal so laut? Wieviel dB erscheinen doppelt so laut zu sein (zweifach)? Hier sind die unterschiedlichen Faktoren. Faktor bedeutet "das Wievielfache", also "wie oft" ... Verdopplung der Lautstärke. |
| Pegel- Änderung |
Lautstärke Lautheit |
Spannung Schalldruck |
Schallleistung Schallintensität |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31,6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2,0 = Verdopplung | 3,16 = √10 | 10 |
| +6 dB | 1,52 fach | 2,0 = Verdopplung | 4,0 |
| +3 dB | 1,23 fach | 1,414 fach = √2 | 2,0 = Verdopplung |
| - - - - ±0 dB - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - - - | - - - - 1,0 - - - - - |
| −3 dB | 0,816 fach | 0,707 fach | 0,5 = Halbierung |
| −6 dB | 0,660 fach | 0,5 = Halbierung | 0,25 |
| −10 dB | 0,5 = Halbierung | 0,316 | 0,1 |
| −20 dB | 0,25 | 0,100 | 0,01 |
| −30 dB | 0,125 | 0,0316 | 0,001 |
| −40 dB | 0,0625 | 0,0100 | 0,0001 |
| Log. Größe | Psychogröße | Feldgröße | Energiegröße |
| dB- Änderung |
Lautstärke- faktor |
Amplituden- faktor |
"Leistungs"- faktor |
| Faktor | Änderung Schall- lautheitspegel |
Änderung Schall- |
Änderung Schall- leistungspegel |
| 20 | +43,22 dB | +26,02 dB | +13,01 dB |
| 15 | +39,07 dB | +23,52 dB | +11,76 dB |
| 10 | +33,22 dB | +20 dB | +10 dB |
| 5 | +23,22 dB | +13,98 dB | +6,99 dB |
| 4 | +20 dB | +12,04 dB | +6,02 dB |
| 3 | +15,58 dB | +9,54 dB | +4,77 dB |
| 2 | +10 dB | +6,02 dB | +3,01 dB |
| - - - - - 1 - - - - - | - - - - ±0 dB - - -- - | - - - - ±0 dB - - - -- | - - - - ±0 dB - - -- - |
| 1/2 = 0,5 | −10 dB | −6,02 dB | −3,01 dB |
| 1/3 = 0,3333 | −15,58 dB | −9,54 dB | −4,77 dB |
| 1/4 = 0,25 | −20 dB | −12,04 dB | −6,02 dB |
| 1/5 = 0,2 | −23,22 dB | −13,98 dB | −6,99 dB |
| 1/10 = 0,1 | −33,22 dB | −20 dB | −10 dB |
| 1/15 = 0,0667 | −39,07 dB | −23,52 dB | −11,76 dB |
| 1/20 = 0,05 | −43,22 dB | −26,02 dB | −13,01 dB |
Lärm
| Lärm ist unerwünschter störender, lästiger oder belästigender Schall. Er ist kein
physikalisches Phänomen, sondern erst psychische Prozesse können ein Geräusch
zu Lärm werden lassen. Es gibt eine Reihe von Lärmdefinitionen. Wichtig dabei sind: 1. die akustischen Faktoren, die das Geräusch charakterisieren und durch messbare physikalische Größen, wie der Amplitude bzw. dem Schalldruckpegel, der Frequenz, sowie dem Zeitverhalten des Schalls beschrieben werden können. 2. die situativen Faktoren, das heißt Ort, Zeitpunkt und Situation, in der sich die Person beim Auftreten des Geräusches befindet und die Relation zu den Aktivitäten, Intentionen und dem momentanen Befinden der Person, die dem Geräusch ausgesetzt ist. 3. die persönlichen Faktoren der Person, die dem Geräusch ausgesetzt ist, mit ihren erworbenen emotionalen und kognitiven Bezügen zur Schallquelle. Die Tatsache, dass Lärm nicht nur von physikalisch messbaren Größen, sondern "von mehr" abhängt, macht die Herleitung von Methoden und Berechnungsverfahren zur objektive Beschreibung der Störwirkung von Geräuschen problematisch und erklärt die Schwierigkeiten der Lärmbekämpfung, die sich oft zwischen den gemessenen Lärmwerten und der empfundenen Belästigung ergeben. Kurt Tucholsky schrieb treffend: "Der eigene Hund macht keinen Lärm - er bellt nur" und "Lärm ist das Geräusch der anderen". |
| Kastrierte Schallpegelwerte in bewerteten dBA werden wie unbewertete Schallpegelwerte in dB addiert. |
| Audiogeräte zeigen in ihren Datenblättern häufig A-bewertete Pegel − nicht weil das mit unserem Gehör übereinstimmen würde − sondern weil damit beispielsweise Brummkomponenten versteckt werden können, die sonst die Werte in einem Datenblatt schlechter aussehen lassen. Worte an helle Köpfe: Immer fragen, was ein Hersteller wohl zu verbergen hat, wenn die A-Frequenzbewertung angegeben wird. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
Formeln beim Arbeiten mit Schall bzw. Lärm
| 1 Pascal (Pa) = 1 Newton/m2 = 10 dyn/cm2 = 10 Mikrobar ≡ 94 dB SPL (Sound Pressure Level) Schalldruckpegel - Sound Pressure Level (SPL) Schalldruckpegel Lp = 20 · lg (p / p0) in Dezibel (dB), wobei p der gemessene Schalldruck als Schallfeldgröße und p0 der Bezugsschalldruck (Referenz) im gleichen Einheitensystem ist: p0 = 20 Mikropascal oder Mikronewton pro m2 = 0,0002 Mikrobar oder dyn pro cm2. Dieser Bezugsschalldruck als Schallfeldgröße gehört zu einer Schallwelle in freier Luft mit einem Schalldruck von p0 = 0,00002 Pa (N/m²). Schallintensitätspegel - Sound Intensity Level (SIL) Schallintensitätspegel II = 10 · lg (I / I0) in Dezibel (dB), wobei I die berechnete Schallintensität als Schallenergiegröße und I0 der Bezugsschallintensität (Referenz) im gleichen Einheitensystem ist: I0 = 10−12 Watt pro m2. Dieser Bezugsschallintensität als Schalleergiegröße gehört zu einer Schallwelle in freier Luft mit einer Schallintensität von I0 = 10−12 Watt/m2. |
Was ist denn Schallpegel?
Eine Reduktion des Schallleistungspegels der Schallquelle um 6 dB führt zu einer Reduktion des
Schalldruckpegels und des Schallintensitätspegels am Ort des Empfängers von ebenfalls 6 dB, auch wenn
die Schallleistung selbst auf den Faktor 0,25 - der Schalldruck aber auf den Faktor 0,5 und die
Schallintensität auf den Faktor 0,25 abgefallen ist. Der Referenzwert (Bezugswert) für den Schallpegel
wurde so gewählt, dass sich bei einer Schallkennimpedanz von Z0 = ρ · c = 400 N·s/m3 für den
Schallintensitätspegel der gleiche Wert ergibt wie für den Schalldruckpegel. Wir sprechen daher einfach
vom "Schallpegel" und lassen offen, ob Schalldruckpegel oder Schallintensitätspegel gemeint ist.
|
| zurück |
Suchmaschine |
Startseite |