Standing waves acoustic resonance and vibrations on ideal strings - Standing waves are stationary waves room modes sound pressure level between hard parallel walls node antinode stationary room acoustic frequency

● 1 - Standing waves (acoustic resonance) on ideal strings ●
Standing waves are stationary waves

The used browser does not support JavaScript.
You will see the program but the function will not work.

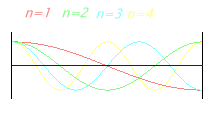
A standing wave is the vibration state of a stable system. An example of this is the
vibrating string of a musical instrument, or the column of air in an organ pipe. These waves
have a “wave-like” look, but nothing is moving. The string is clamped between two fixed
ends with length L; which is called a node also known as a zero crossing. The location
directly between two nodes is called an antinode. Shown below are the natural vibrations
of an idealized string, which is assumed to be perfectly flexible. The stiffness is assumed
to be zero. The frequencies of the vibrations form harmonics, also called partials.
c = speed of sound. L = length of the string.
The fundamental wave is known as the first harmonic.

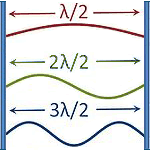
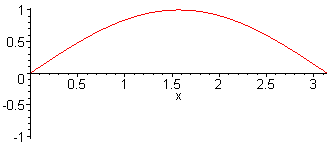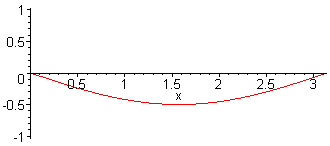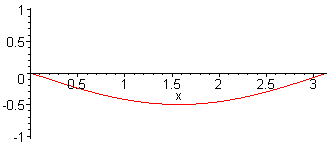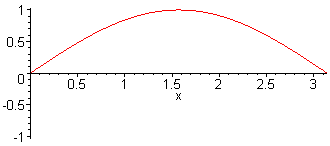1st harm. L = λ/2 = π f₁ = c / (2·L)

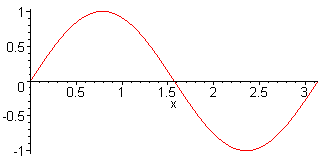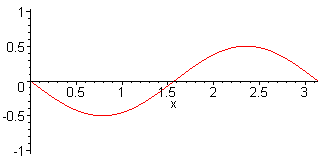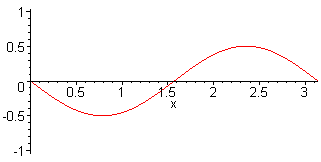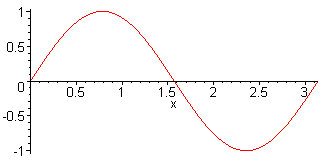2nd harm. L = λ f₂ = 2·f₁ = c / L

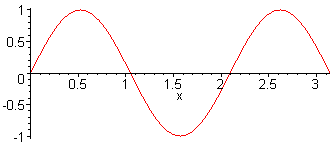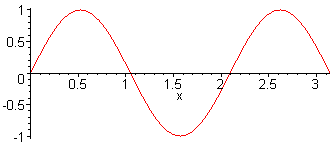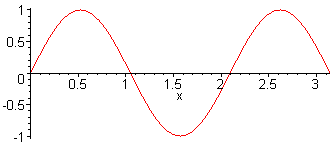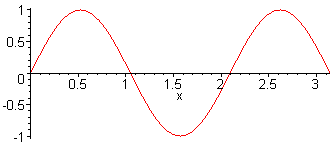3rd harm. L = 3 λ / 2 f₃ = 3·f₁ = 3·c / (2·L)

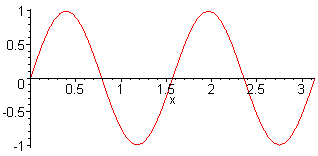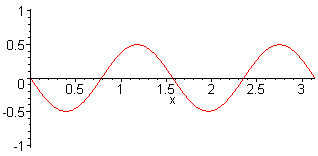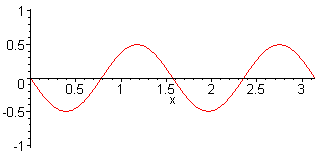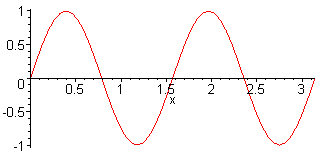4th harm. L = 2 λ f₄ = 4·f₁ = 4·c / (2·L)

Note: Note: The distance between two nodes (knots) or two maxima
(antinodes) is λ/2. The distance between a node (maximum) and an
antinode (minimum) is λ/4.

Note, because there is often confusion:
An antinode in sound pressure (pressure antinode) is at the same time a
node in the displacement of the air particles (particle displacement node).
It is mostly forgotten to tell the viewer of the figures what is shown: sound
pressure derivations or motion of particle displacement. That's a difference.

2 - Standing waves (acoustic resonance) on pipes (flutes)

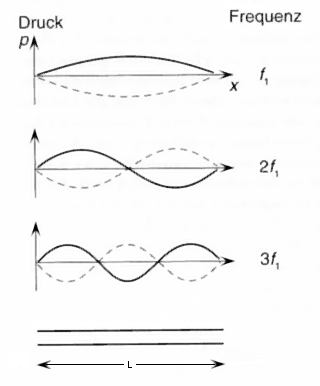Druck = pressure and Frequenz = frequency

1st harm.   L = λ / 2 = π     f₁ = c / (2 · L)

2nd harm.   L = λ                  f₂ = 2 · f₁ = c / L

3rd harm.   L = 3 λ / 2         f₃ = 3 · f₁ = 3 c / (2 · L)

Open tube

Oscillations of a column of air of an open tube (flute). At the open end
theoretically there must be a sound pressure node, if one leaves
aside the end correction.

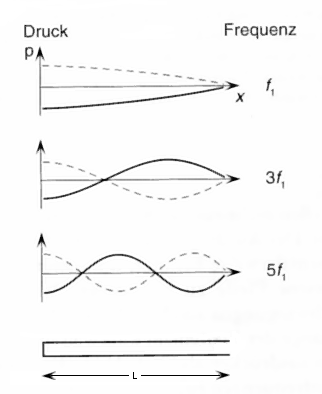Druck = pressure and Frequenz = frequency

1st harm.   L = λ / 4 = π · 1 / 4    f₁ = c / (4 · L)

3rd harm.   L = 3 λ / 4                  f₃ = 3 · f₁ = 3 c / (4 · L)

5th harm.   L = 5 λ / 4                   f₅ = 5 · f₁ = 5 c / (4 · L)

Left single-edge closed tube

Oscillations of an air column of a single-edge closed tube (flute); also stopped
pipe (gedackt). At the closed end theoretically there must be an antinode of the
sound pressure.

There are misunderstandigs of waves in air, because sinusoidal patterns can
indicate the nodes and antinodes of the displacement of the sound, the particle
velocity of the sound, and the sound pressure or the sound density.
Sound engineers using microphones are only interested in the behavior of the
sound pressure deviations.
Notice: A pressure node corresponds to a displacement antinode!

3 - Room modes (standing waves) between sonically hard parallel walls

Where do I set up my speakers? Where is the best listening spot? Where to go with the acoustic treatment?
The following fundamentals for the acoustics of low frequency sound waves in rooms you should know.
This applies to the recording room as well as for the playback room.

The room resonances formed between the boundary surfaces of a room, are called
"standing waves" or room modes, or modes. They arise if a multiple of half the
wavelength (λ/2) fits between the boundary surfaces of an area. Therefore, one need
not necessarily parallel walls. Sound technicians are interested in the behavior of the
sound pressure, because by its effect our eardrums and the microphone
diaphragms are moved, see: Effect and cause.

A standing wave as sound pressure distribution:
3rd harmonic (2nd overtone) − 3 nodes and 4 antinodes

Room modes as sound pressure distribution

Calculation of the three modes (eigenmodes) - resonances of rectangular rooms

An eigenmode (eigentone) is the European name for a standing wave.

Note: In practice only low frequencies as sound pressure below 300 Hz are
considered as room modes. Higher modal frequencies become less important,
because their disturbing effect is masked by other acoustic effects.
On the walls there are formed by the modes always sound pressure maxima -
that are sound pressure antinodes (or particle velocity minima = nodes).

By the following formula standing waves that are room resonances (modes), which are built
between the reverberant boundary surfaces of a rectangular room, can be determined in
their frequency. On a sound-reflecting wall (boundary) the absorption coefficient is α = 0.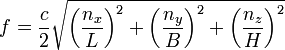

formula room modes

Where:
f = frequency of the mode in Hz
c = speed of sound 343 m/s at 20 °C
n_x = numbers of natural oscillations (room length) (1, 2, 3, ...)
n_y = numbers of natural oscillations (room width) (1, 2, 3, ...)
n_z = numbers of natural oscillations (room height) (1, 2, 3, ...)
L, B, H = length, width and height of the room in meters
A standing wave 1st order of the fundamental frequency = f₁ occurs, when half the
wavelength of the excitation frequency fits between the sonically hard boundary surfaces.
For the axial mode we get the lowest frequency :

f₁ = c / (2 · L)

Where:
c = speed of sound343 m/s at 20 °C
f₁ = frequency in Hz of the axial mode
L = longest distance in meters of the boundary surfaces.

The standing waves of higher order are calculated from the integer multiples of the
1st order mode.
f₂ = 2 · f₁
f₃ = 3 · f₁
f₄ = 4 · f₁

Antinodes pressure maximum	Nodes zero crossing	Wavelength	Frequency	Harmonics	Overtones
2	1	λ = 2 × L	f₁ = 1 × c / (2 × L)	1st harmonic	fundamental

3	2	λ = L	f₁ = 2 × c /(2 × L)	2nd harmonic	1st overtone

4	3	λ = (2 × L) / 3	f₁ = 3 × c / (2 × L)	3rd harmonic	2nd overtone

k + 1	k	λ = (2 × L) / k	f₁ = k × c / (2 × L)	k harmonic	(k − 1) overtone

k = 1, 2, 3, ...

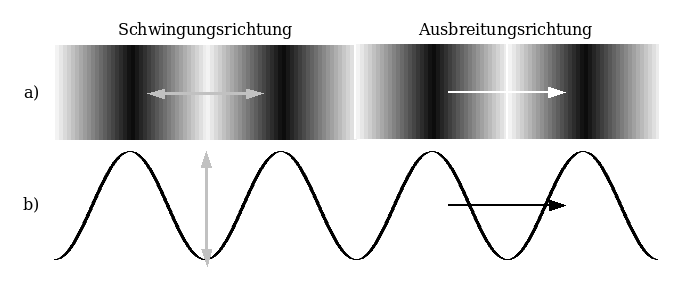
The sound pressure is actually a longitudinal wave a),
in contrast to this more presentable transverse wave b).

Direction of oscillation Direction of propagation

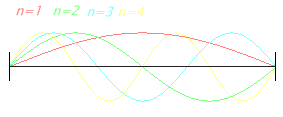
Standing wave modes as sound pressure distribution
between the walls. Wave with two open ends.

1st harm. L = λ/2 = π f₁ = c / (2·L)

2nd harm. L = λ f₂ = 2·f₁ = c / L

3rd harm. L = 3 λ / 2 f₃ = 3·f₁ = 3·c / (2·L)

4th harm. L = 2 λ f₄ = 4·f₁ = 4·c / (2·L)

Here, the sound pressure of a sine wave with harmonics is presented
between two totally reflecting walls which in reality is a longitudinal wave.
It is important that in the case of resonance there is always a
maximum sound pressure on the walls. In many figures this is wrongly
shown as a vibration of a string, which has always a fixed node (knot) at
each end, as in the following example:

This is not the representation
of sound pressure vibrations
between walls in a small room.

These are vibrations of a string
(displacement amplitudes).

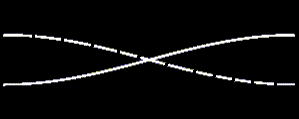
A typical wrong figure with
nodes at the walls.

Showing the air displace-
ment was not desired.

A string is clamped between two "fixed ends". At the ends will be a wave node.
A wave between two hard walls is considered as a sound pressure with "loose ends".
Therefore on the sides of the wall there appears as sound pressure a wave maximum
or an antinode.

Not good: Standing Wave - Wikipedia and Resonant room modes - Wikipedia
This is correct : From Wikibooks, the open-content textbooks collection

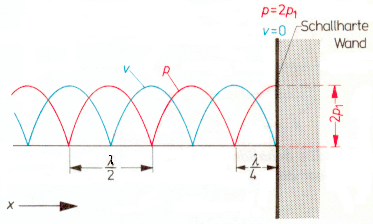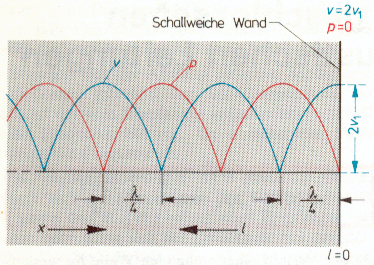
Sonically hard wall

Spatial distribution of sound pressure p (red) and particle velocity v (blue) in a
schematized standing wave with total reflection from a sonically hard wall.
At a distance of λ / 4 from the wall the sound pressure is p = 0.
Since the absorption effect increases in a material with the sound velocity,
the absorber should be effective in the velocity maximum at the distance of λ / 4
from the wall or should have an appropriate density. Much easier measurable is
the sound pressure minimum, at the exact spot of velocity maximum.

Here is a nice animation of a standing wave - Explanation by
superposition with the reflected wave. This setting must be:
"Reflection from a free end".
http://www.walter-fendt.de/ph14e/stwaverefl.htm

Conclusion:
The vibrations of sound pressure between parallel walls in
standing waves as room modes are looking much different
with "open ends" at the walls (antinodes) than the vibrations
of strings between two "fixed ends" (nodes).

Remember:
At reflective walls (boundaries) we find always the maximum
sound pressure, a so called wave antinode.
This is also the principle of the boundary layer microphones.

The frequency at which the first (lowest) room mode occurs, is calculated using the
following formula: Frequency = speed of sound c / (longest room dimension × 2)

Comparison of the reflections in an echo chamber
and an extremely highly damped room.

Sound pressure reflections (modes) at sonically hard walls, like in an echo chamber (wet).

Sound pressure reflections (modes) at sonically soft walls, like in a reflection free room (dry).

Sonically soft wall

Spatial distribution of sound pressure p (red) and particle velocity v (blue) in
a schematized standing wave with total reflection from a sonically soft wall.
At a distance of λ / 4 from the wall the sound pressure is p = maximum.

A typical room (control room) with axial modes and sound pressure anti nodes at the walls

Room Eigenmodes Calculator − Jörg Hunecke
This calculator determines the room eigenmodes with the 20 lowest eigenfrequencies
for rectangular rooms and presents them in ascending order.

The Pressure Chamber Effect

Even below the lowest room mode low frequencies are reproducible.
One uses the pressure chamber effect in a with hard boundary surfaces
equipped small room, where the room must be sealed pressure-tight.
The "dB Drag Racing" fans need that for their car loudness competitions.

RPG Triffusor

Absorption - Reflection - Diffusion - Combination

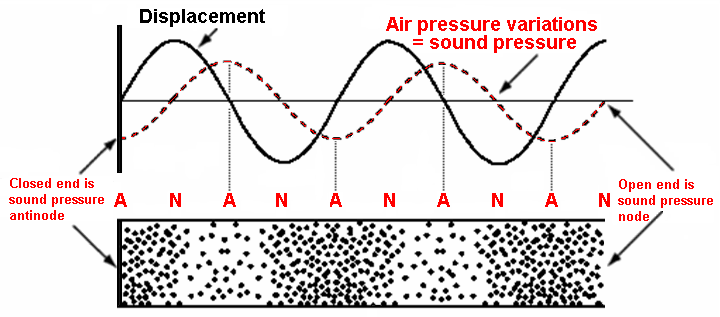Displacement sound pressure node antinode

Notice: At a hard reflecting wall (closed end) there is a sound
pressure antinode but at the same time there is a particle
displacement node. When one speaks of standing waves, it must be
expressed clearly that we mean amplitudes of the acoustic pressure
changes that move our eardrums.
That is mostly forgotten. The sound pressure derivtions of air are
oscillating with antinodes and nodes - at the same time the
displacement of air particles are oscillating with nodes and
antinodes.
The relationship between the maximum pressure change Δ p_m
and the maximum displacement amplitude of the air particles ξ_m is:
Δ p_m = (v ρ ω) ξ_m.

Amplitudes of the Soundfield Quantities of a Plane Wave

Distinguish the amplitudes of particle displacement, sound pressure, sound
velocity, and pressure gradient.
Sound pressure antinode is particle displacement node of the air particles.
Particle displacement antinode of the air particles is sound pressure node.

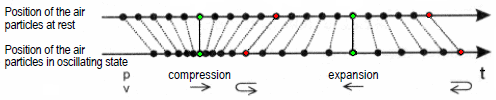At rest, a green air particle has the same position as in the oscillation
condition. The displacement of air particles is going through a zero
crossing while the sound pressure amplitude with p maximum
(condensation, compression) or a minimum (rarefaction, expension)
shows. At rest, a red air particle is at the maximum or minimum of the
amplitude of the same time there is a zero crossing of the sound
pressure wave. Thus, there the sound pressure is zero; ie the normal
static air pressure is present alone.

In graphic representations of standing waves (room modes) between two
walls, usually there is not specified whether there is shown the sound
pressure as the pressure variation in the air, or the displacement of the air.
However, this clarification is really necessary.
The figures above show the important difference.
Left = sound pressure (antinodes) and right = displacement (nodes).

Notice: The effect of standing waves reports our hearing, but the sound
pressure deviations (fluctuations, variations) move effectively our eardrums.

back

Search Engine

home