

| English version |
| Rges | 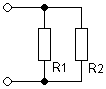 |
Formel: Rges = R1·R2/(R1+R2) |
Gleichung oder Formel für die Berechnung der Parallelschaltung zweier Widerstände R1 and R2:
![]()
![]()
Berechnung des notwendigen Parallelwiderstands R2, wenn R1 und der Gesamtwiderstand Rges gegeben ist:

|
Auflösen der Formel Rges= (R1· R2) / (R1 + R2) nach R1: 1/Rges = 1/R1 + 1/R2 Rges · R1 · R2[1/Rges = 1/R1 + 1/R2] R1 · R2 = Rges · R2 + Rges · R1 R1 · R2 − Rges · R1 = Rges · R2 R1(R2 − Rges) = R2 · Rges Letzter Schritt: R1 = R2 · Rges / (R2 − Rges) beziehungsweise: R2 = R1 · Rges / (R1 − Rges) |
Merke: Berechnung der Parallel-Widerstände ist genau das Gleiche, wie die Berechnung
der Parallelschaltung von Spulen oder die Reihenschaltung von Kondensatoren.
![]()
• Suche die Widerstände R1 und R2, wenn der Gesamtwiderstand bekannt ist: •
Berechnung: Widerstand-Parallelschaltung durch Iteration
Finden von R1 und R2 bei bekanntem Gesamt-Widerstand
![]()
● Berechne viele parallele Widerstände ●
| Hier kann man den Gesamt-Widerstand berechnen - bis zu 10 parallelgeschaltete Widerstände. Gib die Widerstandswerte in die unteren Felder ein und wenn alle Werte eingegeben sind, dann klicke auf 'Berechnung'. Das Ergebnis wird darunter angegeben. Als Test kann man einmal die Werte 4, 6 und 12 Ohm eingeben; das Ergebnis sollte 2 Ohm sein. Achtung: Das Leeren der Felder von Hand löscht nicht die gespeicherten Werte. |
Das Ohmsche Gesetz - Ohmsches Gesetz
Zwei parallelgeschaltete Widerstände und der berechnete Gesamtwiderstand
Widerstände von 1 bis 100 Ohm
| R2 | R1 | |||||||||||
| 1 | 1,5 | 2,2 | 3,3 | 4,7 | 6,8 | 10 | 15 | 22 | 33 | 47 | 68 | |
| 1 | 0,5 | 0,6 | 0,69 | 0,77 | 0,83 | 0,87 | 0,91 | 0,93 | 0,95 | 0,97 | 0,98 | 0,99 |
| 1,5 | 0,6 | 0,75 | 0,89 | 1,03 | 1,14 | 1,22 | 1,30 | 1,36 | 1,40 | 1,43 | 1,45 | 1,46 |
| 2,2 | 0,69 | 0,89 | 1,1 | 1,32 | 1,50 | 1,66 | 1,82 | 1,92 | 2,0 | 2,06 | 2,10 | 2,13 |
| 3,3 | 0,77 | 1,03 | 1,32 | 1,65 | 1,94 | 2,22 | 2,48 | 2,70 | 2,87 | 3,00 | 3,08 | 3,14 |
| 4,7 | 0,83 | 1,14 | 1,50 | 1,94 | 2,35 | 2,78 | 3,20 | 3,58 | 3,87 | 4,12 | 4,27 | 4,39 |
| 6,8 | 0,87 | 1,22 | 1,66 | 2,22 | 2,78 | 3,40 | 4,05 | 4,68 | 5,19 | 5,64 | 5,94 | 6,18 |
| 10 | 0,91 | 1,30 | 1,82 | 2,48 | 3,20 | 4,05 | 5,0 | 6,0 | 6,9 | 7,7 | 8,3 | 8,7 |
| 15 | 0,93 | 1,36 | 1,92 | 2,70 | 3,58 | 4,68 | 6,0 | 7,50 | 8,9 | 10,3 | 11,4 | 12,2 |
| 22 | 0,95 | 1,40 | 2,00 | 2,87 | 3,87 | 5,19 | 6,9 | 8,9 | 11,0 | 13,2 | 15,0 | 16,6 |
| 33 | 0,97 | 1,43 | 2,06 | 3,0 | 4,12 | 5,64 | 7,7 | 10,3 | 13,2 | 16,5 | 19,4 | 22,2 |
| 47 | 0,98 | 1,45 | 2,1 | 3,08 | 4,27 | 5,94 | 8,3 | 11,4 | 15,0 | 19,4 | 23,5 | 27,8 |
| 68 | 0,99 | 1,46 | 2,13 | 3,14 | 4,39 | 6,18 | 8,7 | 12,2 | 16,6 | 22,2 | 27,8 | 34,0 |
Hinweis: Dieser Rechner kann auch andere mathematische Probleme lösen.
Berechnung von parallelel-geschalteten Widerständen ist genau das gleiche wie
die für parallel-geschaltete Induktivitäten oder in Reihe geschaltete Kondensatoren.
| Umgesetzte Leistung in einem Widerstand: P = U · I, P = U2 / R, P = I2 · R. |
| Merke: Für die Widerstände in Reihe ist der Strom für jeden Widerstand der gleiche und für Widerstände in Parallel, ist die Spannung für jeden Widerstand die gleiche. |
| zurück |
Suchmaschine |
Startseite |