

| English version |
| Die folgende Tabelle fasst die Eigenschaften der stehenden Welle des Schalls
in Luft als Schalldruck p für die erste "Harmonische" zwischen zwei harten
reflektierenden Wänden zusammen. Dieses sollten Tontechniker schon kennen. Die 1. Harmonische ist die Grundschwingung (Frequenz) der stehenden Welle. |
nische |
der Knoten |
der Bäuche |
Darstellung Raum-Wände |
Beziehung |
| Die folgende Tabelle fasst die Eigenschaften der stehenden Welle als Teilchen-Auslenkung ξ (Amplitude) für die ersten Harmonischen einer eingespannten Saite zusammen, die an beiden Endpunkten fixiert sein muss. |
nische |
der Knoten |
der Bäuche |
Darstellung einer Saite |
Beziehung |
| In der Abbildung ganz oben wird der Schallwechseldruck einer Sinusschwingung
und ihren Harmonischen zwischen zwei total schallreflektierenden, d. h.
schallharten Wänden dargestellt. Wichtig ist, dass sich im Resonanzfall an den
Wänden immer ein Schalldruckmaximum (Schalldruckbauch) befindet. In einigen Darstellungen zur Erklärung der Raummoden wird unrichtig die Abbildung der Saitenschwingung verwendet, die dann an jedem Ende immer einen festen Knoten hat, wie z. B. hier: |
| Dieses sind keine Darstellungen von Schalldruckschwingungen zwischen zwei Wänden in einem kleinen Raum ... ... sondern das sind Saiten- schwingungen (Amplituden). |
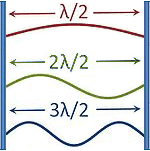 |
Eine typische Falschdarstellung mit Knoten an den Wänden. Die Darstellung der Schallauslenkung war nicht gewünscht. |
| Eine Saite ist zwischen zwei "festen Enden" eingespannt. An den Enden erscheint ein Wellenknoten. Eine Welle zwischen zwei harten Wänden wird beim Schalldruck mit "losen Enden" betrachtet. Daher erscheint als Schalldruck an den Wandseiten ein Wellenmaximum bzw. ein Wellenbauch. Bei den Raummoden interessiert uns Tontechniker allein die Amplitude des Schalldrucks p (Schalldruckamplitude), denn diese Größe bewegt unsere Trommelfelle und lässt uns damit die störenden tieffrequenten Raummoden hören. Weniger beachten sollten wir die Amplitude der Schallauslenkung ξ (Amplitude der Teilchenauslenkung der Luft), die Amplitude der Schallschnelle v (Amplitude der Teilchengeschwindigkeit) = Geschwindigkeitsamplitude der Teilchen und die Amplitude des Druckgradienten Δ p; siehe: "Was ist eine Amplitude?" und "Die Schallfeldgrößen einer ebenen Welle − Die Amplituden". |
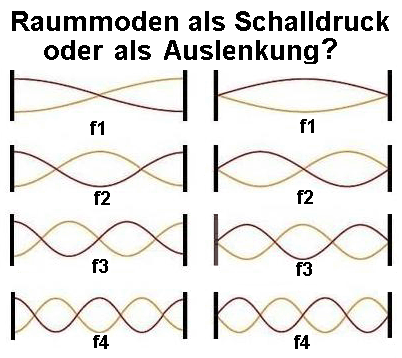
| Zur Beachtung, denn es gibt häufig Verwirrung: Ein Bauch beim Schallwechseldruck (pressure antinode) ist zur gleichen Zeit (!) ein Knoten bei der Auslenkung der Luftteilchen (particle displacement node). Es ist ein Problem, dass überwiegend vergessen wird, dem Betrachter der Abbildungen zu sagen, worum es sich handelt: um den Schallwechseldruck oder um die Bewegung der Auslenkung von Luftteilchen. |
 |
| Eine stehende Welle ist der Schwingungszustand eines zusammenhängenden Systems. Als
Musterbeispiel wird dafür üblicherweise die schwingende Saite eines Musikinstruments oder die
Luftsäule in einer Orgelpfeife genommen. Diese Wellen haben zwar ein wellenartiges Aussehen,
bewegen sich aber nirgendwohin; d. h. sie schwingen zeitlich aber nicht örtlich − sie sind ortsfest. Die Saite ist mit einer Länge L zwischen zwei festen Enden eingespannt, an denen sich immer ein Schwingungsknoten befindet. Zwischen diesen beiden Knoten (Nulldurchgang) ergibt sich ein Maximum, das auch Schwingungsbauch oder Wellenbauch genannt wird. |
| Wo stelle ich meine Lautsprecher hin? Wo ist der beste Abhörplatz? Wohin mit der akustischen
Dämpfung? Folgende Grundlagen zur Akustik der Schallwellen bei tiefen Frequenzen in Räumen sollte man dazu kennen. Das gilt für den Aufnahmeraum genauso wie für den Wiedergaberaum = Regieraum oder das Wohnzimmer. |
| Die Raumresonanzen, die sich zwischen den Begrenzungsflächen eines Raumes bilden,
nennt man "stehende Wellen" oder Raumeigenmoden, auch kurz Moden. Sie entstehen,
wenn ein Vielfaches der halben Wellenlänge (λ/2) zwischen die Begrenzungsflächen
eines Raums passt. Voraussetzung für eine Raummode ist eine stehende Welle. Uns Tontechniker interessiert das Verhalten des Schalldrucks, weil durch seine Wirkung unsere Trommelfelle und die Mikrofonmembranen bewegt werden; siehe: Die Wirkung und die Ursache beim Schall. Raummoden sind nichts anderes als stehende Wellen, die sich in jedem Raum bei tiefen Frequenzen unter 300 Hz ausbilden. Nicht-parallele Wände sind kein Mittel dagegen. |
| Die Ausbildung von stehenden Wellen im Raum an schallharten Wänden
(Raummoden) ist von den Saitenschwingungen zwischen zwei fest
eingespannten Punkten klar zu unterscheiden. Für schwingungsfähige Systeme gilt allgemein, dass die Amplitude, genauer die Schalldruckamplitude viel stärker ausgeprägt ist, wenn die Erregung mit einer Eigenfrequenz des Systems erfolgt. Dieser Spezialfall wird in der Physik allgemein als Resonanz bezeichnet; siehe: "Stehende Wellen und akustische Resonanz bei idealen Saiten": http://www.sengpielaudio.com/StehendeWellen.htm "Berechnen der drei Moden (Raumeigenmoden) − Raumresonanzen von Rechteck-Räumen": http://www.sengpielaudio.com/Rechner-raum-moden.htm Zwischen zwei zueinander parallelen Wänden wird eine Schallwelle hin und her reflektiert. Bei einer bestimmten Wellenlänge λ = 2 · L (L = Raum- Länge, Breite oder Höhe) passen beide Wellen exakt übereinander und prägen eine stehende Welle voll aus. Wenn der Abstand der parallelen Wände gerade dem Vielfachen der halben Wellenlänge entspricht, dann gibt es 'stehende' Wellen, also eine Schalldruckerhöhung. Die Frequenz, bei der das passiert, nennt man auch Resonanzfrequenz oder Raummode. Bei Frequenzen, die nicht ein Vielfaches dieser Frequenz sind, befinden sich die Schalldruckmaxima an verschiedenen Stellen, wodurch sich die Effekte zum Teil aufheben und sich stehende Wellen wenig ausprägen oder gar auslöschen. Praktisch werden nur tiefe Frequenzen unterhalb von 300 Hz als Raummoden hörbar auffällig. Höhere modale Frequenzen verlieren an Bedeutung, denn ihre Störwirkung wird durch andere raumakustische Effekte überdeckt. In der Nähe von reflektierenden Wänden zeigen sich als Moden immer Schalldruckmaxima − das sind Wellenbäuche, wenn der wirksame Schalldruck betrachtet wird. |
| zurück |
Suchmaschine |
Startseite |