

| Deutsche Version |
1 – Sensitivity (new): dB re 1 V/Pa ← → Transfer factor: mV/Pa
| International standards have established 1 pascal (Pa) as 94 dBSPL (sound pressure level). This reference point is now accepted for specifying the sensitivity of microphones. The μbar found in some non-European specifications refers to 74 dBSPL (20 dB less than 1 Pa) and the sensitivity or the sensitivity factor is not expressed as transfer factor in the usual form of "mV/Pa" as open circuit voltage rating. In the data sheets the sensitivity always applies to the frequency 1 kHz, unless otherwise noted. Microphones simply convert the sound pressure deviations p (pascal Pa) to audio voltage V (volts V). Forget necessarily the energy as output power of the microphone! |
| Transfer factor, at 1 kHz and 1 Pa ≡ 94 dB SPL M = 50 mV/Pa or Sensitivity (level), dB re 1V/Pa (1 kHz) LM = 20 × log10 (M/MR) = −26 dBV with MR = 1V/Pa |
![]()
2 – Sensitivity (old): dB re 1 V/dyne/cm2 ← → Transfer factor: mV/Pa
| Microphone firms in the USA are partly still using the old sensitivity of "dB re 1 V/dyne/cm2" or "dB re 1 V/µbar" (74 dBSPL) and do not show the usual form "mV/Pa". In the data sheets the sensitivity always applies to the frequency 1 kHz, unless otherwise noted. |
| 1 µbar = 1 dyne/cm2 = 0.1 Pascal and 1 pascal = 10 µbars = 10 dynes/cm2 1 mV/µbar or 1 mV/Pa = 0.1 mV/µbar = 10 mV/Pa and pascal = newton/m2 |
| Pascal is written in English with lower-case letter beginning: We have the pascal and we
have the dyne, and the plural dynes which are microbars. A typical condenser microphone,
having 10 mV/Pa is the same as 1.0 mV/µbar; but 10 Pa are 100 µbar. −40 dB "re 1V/Pa" equals to −60 dB "re 1V/microbar". There is a difference of 20 dB. The sound pressure p is precisely the sound pressure as an effective value (RMS). |
| All field quantities, like voltage, or sound pressure are always RMS values in audio engineering, unless otherwise stated. |
| An often heard question: Why are microphone output levels
expressed in negative decibels (dB)? Answer: Because all microphones produce a voltage level which is less than 1 volt ≡ 0 dB for the reference sound pressure level of 94 dB or 74 dB. |
| The sensitivity (transfer factor) in mV / Pa shows clearly that microphones change sound pressure (Pa) to audio voltage (mV). Energy and power play no role for these microphone transducers. Our eardrums are also moved by the sound pressure deviations. Sound pressure as a sound field quantity cannot be the same like acoustic intensity or sound power as a sound energy quantity. |
| At the output of microphones there is no output power to find. |
|
Forget the power ratings. They have no relevance to microphones. The term "dB SPL" is a measurement
of Sound Pressure Level, or SPL which is the force per area that acoustical sound waves apply to air
particles. Microphones are sensors in the sound field which deliver an analogous voltage. Microphones
measure sound pressure, or sometimes they may measure the particle velocity, but they never measure
sound intensity directly. Intensity stereo is an unfortunate linguistic misnomer which has come to mean the
recording of stereophonic signals that are distinguished only by level differences. In stereo the level
differences have been called "intensity" differences, but sound intensity is a specifically defined quantity
and cannot be sensed by a simple microphone, nor would it be valuable in music recording if it could.
"Intensity" stereophony is a misnomer and is better called level difference stereophony. Ears
(earsdrum) are directly sensitive to sound pressure, like microphones (diaphragm). Forget both
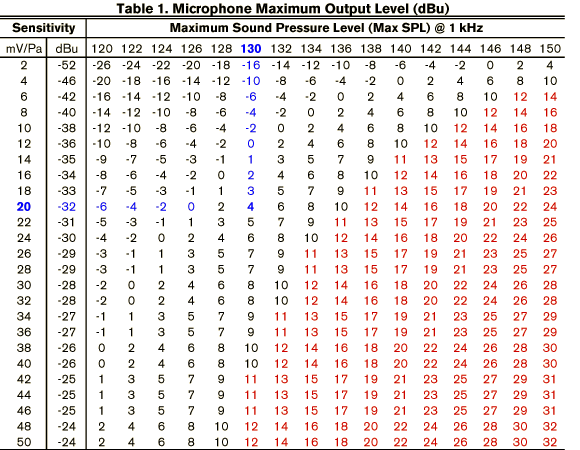
intensity and the power. A studio microphone is never attached to a load equal to its own internal resistance. The load resistor (impedance) should always to be at least ten times greater than the internal source resistor of the microphone (open circuit). Here only voltage is important and not the power. Sound intensity and energy are both energy and power quantities as well as computational tools for acousticians and sound protectors (noise fighters), and not so important for sound engineers. Note: The output voltage of a microphone is proportional to the incident sound pressure. To obtain the microphone maximum output level in dBu, find your microphone's sensitivity rating on the left side and then move right until you are directly below your microphone's maximum SPL rating. As an example, for a microphone with a sensitivity rating of 20 mV/Pa and a max SPL equal to 130 dB. Table 1 tells us that the maximum output voltage is +4 dBu. You now have what you need to compare preamps regarding maximum input level. |
 |
Microphone Dynamic Range Calculation
| Enter any TWO of the following values, then press the calculate button. The missing value will be calculated. 10 μbar = 1 pascal ≡ 94 dBSPL rating is used here. |
| Self-noise may be entered using any weighting factor (A, CCIR 468 etc.) but
the dynamic range will be predicated by that weighting. "S/N re 94 dB SPL" is 94 dB minus self noise. The max. SPL for less than 0.5 % THD should be used. If you find there values for 1 % THD, then do a 6 dB subtraction, for a more correct comparison. |
| Note: There is no conversion formula for weighted dBA values to sound pressure level dBSPL or vice versa. |
| Pro audio equipment often lists an A-weighted noise spec − not because it correlates well with our hearing − but because it can "hide" nasty hum components that make for bad noise specs. Words to bright minds: Always wonder what a manufacturer is hiding when they use A-weighting. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane
Readings of a pure 1 kHz tone should be identical, whether weighted or not.
Transfer factor in mV/Pa and sensitivity
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
The sensitivity must be a negative dB value.
The sometimes found microphone "power level" in dB is wrong.
It really has to be "sensitivity in dB re 1 V/Pa".
Interconnection of microphone and preamplifierZout < Zin
Data of condenser microphones in comparison
| The sensitivity (transfer factor) in mV / Pa shows clearly that microphones are sensors and change sound pressure (Pa) to audio voltage (mV). Energy and power plays no role for this microphone transducers. Our eardrums are effectively moved by the sound pressure deviations. Sound pressure as sound field quantity cannot be the same as sound intensity as sound energy quantity. |
| "Input sensitivity" is basically the same thing as sensitivity - putting the word "input" in front of it is somewhat redundant. Input sensitivity controls are commonly found on amplifiers and other audio equipment, but not on microphones. |
Conversion of sound units (levels)
Acoustic equivalent for ohm's law
|
|
| In the "Specification Data" you will not find the word "electret microphone" because this fact is hidden by the term "pre-polarized condenser microphone". |
| back |
Search Engine |
home |