Note names of musical notes keyboard piano frequencies = octave piano keys number tone tones 88 notes frequency names of all keys on a grand piano standard concert pitch tuning German English system MIDI 88

● Keyboard and frequencies ●
● Naming of musical notes and piano keys ●

Music notation systems − Music frequencies of equal temperament tuning

Chord name finder by note entry

The English and American scientific system versus the German system
Scientific Pitch Notation (SPN), also known as American Standard Pitch Notation

The standard pitch tuning is A4 (A above middle C) − in German-speaking countries it is called a’.
The notes have different names. The German system is used also in many other countries, as there are
e.g. Poland, Czech Republic, and Russia.
A "normal" piano has the following dimensions: width 145 to 150 cm, height 115 to 125 cm, depth 52 to 60 cm.
A typical "keyboard" has 61 keys today. The sound frequencies of the 88 keys on the piano are:

Piano key number	English notation	German notation	Frequency Hz
88	C8 - Last tone	c’’’’’ - Highest	4186.01
87	B7	h’’’’	3951.07
86	A7/B7	ais’’’’/b’’’’	3729.31
85	A7	a’’’’	3520.00
84	G7/A7	gis’’’’/as’’’’	3322.44
83	G7	g’’’’	3135.96
82	F7/G7	fis’’’’/ges’’’’	2959.96
81	F7	f’’’’	2793.83
80	E7	e’’’’	2637.02
79	D7/E7	dis’’’’/es''''	2489.02
78	D7	d’’’’	2349.32
77	C7/D7	cis’’’’/des’’’’	2217.46
76	C7	c’’’’	2093.00
75	B6	h’’’	1975.53
74	A6/B6	ais’’’/b’’’	1864.66
73	A6	a’’’	1760.00
72	G6/A6	gis’’’/as’’’	1661.22
71	G6	g’’’	1567.98
70	F6/G6	fis’’’/ges’’’	1479.98
69	F6	f’’’	1396.91
68	E6	e’’’	1318.51
67	D6/E6	dis’’’/es’’’	1244.51
66	D6	d’’’	1174.66
65	C6/D6	cis’’’/des’’’	1108.73
64	C6 (high C)	c’’’	1046.50
63	B5	h’’	987.767
62	A5/B5	ais’’/b’’	932.328
61	A5	a’’	880.000
60	G5/A5	gis’’/as’’	830.609
59	G5	g’’	783.991
58	F5/G5	fis’’/ges’’	739.989
57	F5	f’’	698.456
56	E5	e’’	659.255
55	D5/E5	dis’’/es’’	622.254
54	D5	d’’	587.330
53	C5/D5	cis’’/des’’	554.365
52	C5	c’’	523.251
51	B4	h’	493.883
50	A4/B4	ais’/b’	466.164
49	A4 concert pitch	a’ Kammerton	440.000
48	G4/A4	gis’/as'’	415.305
47	G4	g’	391.995
46	F4/G4	fis’/ges’	369.994
45	F4	f’	349.228
44	E4	e’	329.628
43	D4/E4	dis’/es’	311.127
42	D4	d’	293.665
41	C4/D4	cis’/des’	277.183
40	C4 (middle C)	c’ (Schloss-C)	261.626
39	B3	h	246.942
38	A3/B3	ais/b	233.082
37	A3	a	220.000
36	G3/A3	gis/as	207.652
35	G3	g	195.998
34	F3/G3	fis/ges	184.997
33	F3	f	174.614
32	E3	e	164.814
31	D3/E3	dis/es	155.563
30	D3	d	146.832
29	C3/D3	cis/des	138.591
28	C3	c	130.813
27	B2	H	123.471
26	A2/B2	Ais/B	116.541
25	A2	A	110.000
24	G2/A2	Gis/As	103.826
23	G2	G	97.9989
22	F2/G2	Fis/Ges	92.4986
21	F2	F	87.3071
20	E2	E	82.4069
19	D2/E2	Dis/Es	77.7817
18	D2	D	73.4162
17	C2/D2	Cis/Des	69.2957
16	C2 (low C)	C	65.4064
15	B1	,H	61.7354
14	A1/B1	,Ais/,B ~60 Hz	58.2705
13	A1	,A	55.0000
12	G1/A1	,Gis/,As	51.9130
11	G1	,G ~50 Hz	48.9995
10	F1/G1	,Fis/,Ges	46.2493
9	F1	,F	43.6536
8	E1	,E	41.2035
7	D1/E1	,Dis/,Es	38.8909
6	D1	,D	36.7081
5	C1/D1	,Cis/,Des	34.6479
4	C1	,C	32.7032
3	B0	,,H	30.8677
2	A0/B0	,,Ais/,,B	29.1353
1	A0 - First tone	,,A - Lowest	27.5000

In the twelve-semitone scale the frequency of the next semitone (halftone) is higher by
the factor of twelfth root of two = 1.0594630943592952645618252949463 or lower by
the factor 0.94387431268169349664191315666757.

A sound engineer should know the following: The AC hum of 50 Hz in Europe is close to
the pitch of G1 = 48.99 Hz (49 Hz). The AC hum of 60 Hz in the U.S. is a minor third higher
close to the pitch of A

1/B

1 = 58.27 Hz (58 Hz).
So you can find out logically, whether a sound recording was made in Europe or in the U.S.

A pure tone with the frequency f = 440 Hz has the amplitude function:
A = sin (880 π×t) - where t is given in seconds.

The following equation will give the frequency f of the
nth piano key number, as shown in the table:
$f(n) = 440\ (\sqrt[12]{2}\,)^{n-49}\,$
Alternatively, this can be written as:
$f(n) = 440 \times 2^{\frac{n-49}{12}}\,$

"Middle C" is in any case only approximately in the middle for the
modern concert piano. For most other instruments it is not in the middle
at all. It is is the lowest note on the standard flute, almost the highest note
on the bassoon. Notationally it is the point of symmetry between the
treble and bass staffs (the current position of the clefs being relatively
modern inventions, and relative to modern human vocal ranges); that is
the only other sense in which it is "in the middle".

Notes and keyboard

The concert pitch A₄ = a’ on the piano lies in the
octave between C₄= c’ (middle C) and C₅= c’’.

The middle C note as octave C₄ and the next octave C₅.

"Middle C" is designated C₄ in scientific pitch notation with a frequency of 261.6 Hz,
because of the note's position as the fourth C key on a standard 88 key piano keyboard.

Some manufacturers label the 440 Hz concert pitch not correctly as A3. It is really A4.
Cubase, Akai, and ProTools are starting differently at octave −2, or octave 1. That's not the standard.
The first tone is the note A0 and that is 27.5 Hz. The classical music world is counting this way.
The tuning pitch for the Western music (concert pitch), is 440 Hz. It is named A4 or a’.

Musical note A4: http://www.wolframalpha.com/input/?i=musical+note+A4&lk=1

Name and frequency of the octave positions
English	A0	A1	A2	A3	A4	A5	A6	A7	A8
German	,,A	,A	A	a	a’	a’’	a’’’	a’’’’	a’’’’’
Frequency in Hz	27.5	55	110	220	440	880	1760	3520	7040

Numbers of the lowest c note for the respective musical octave.

Ranges of some popular instruments

Instrument	Start	End
guitar	E2	E6
seven string guitar	B1	E6
cello	C2	A6
4-string bass guitar	E1	E5
piano	A0	C8
piccolo	C5	C8
violin	G3	E7

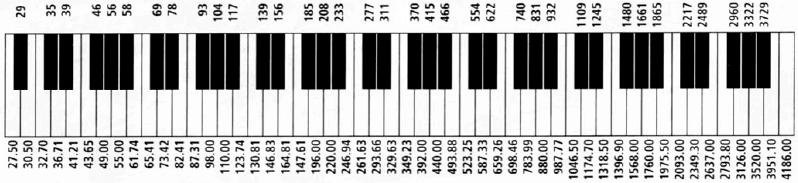
All piano keys

Frequencies of the equal temperament − table or chart
Octave	0	1	2	3	4	5	6	7	8	9	10
C / B#	16.352	32.703	65.406	130.813	261.626	523.251	1046.502	2093.005	4186.009	8372.018	16744.036
C# / Db	17.324	34.648	69.296	138.591	277.183	554.365	1108.731	2217.461	4434.922	8869.844	17739.688
D	18.354	36.708	73.416	146.832	293.665	587.330	1174.659	2349.318	4698.636	9397.273	18794.545
D# / Eb	19.445	38.891	77.782	155.563	311.127	622.254	1244.508	2489.016	4978.032	9956.063	19912.127
E / Fb	20.602	41.203	82.407	164.814	329.628	659.255	1318.510	2637.020	5274.041	10548.082	-
F / E#	21.827	43.654	87.307	174.614	349.228	698.456	1396.913	2793.826	5587.652	11175.303	-
F# / Gb	23.125	46.249	92.499	184.997	369.994	739.989	1479.978	2959.955	5919.911	11839.822	-
G	24.500	48.999	97.999	195.998	391.995	783.991	1567.982	3135.963	6271.927	12543.854	-
G# / Ab	25.957	51.913	103.826	207.652	415.305	830.609	1661.219	3322.438	6644.875	13289.750	-
A	27.500	55.000	110.000	220.000	440.000	880.000	1760.000	3520.000	7040.000	14080.000	-
A# / Bb	29.135	58.270	116.541	233.082	466.164	932.328	1864.655	3729.310	7458.620	14917.240	-
B / Cb	30.868	61.735	123.471	246.942	493.883	987.767	1975.533	3951.066	7902.133	15804.266	-

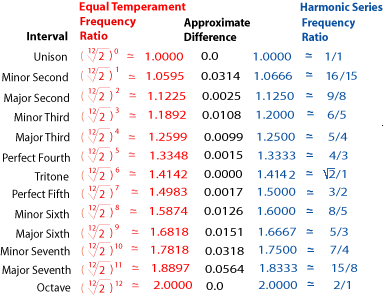
Comparing the Frequency Ratios for Equal Temperament and Pure Harmonic Series

Size (Measure) of all Steinway Grand Pianos

Type	Length	Width	Height
S	155 cm	147 cm	101 cm
M	170 cm	147 cm	101 cm
O	180 cm	147 cm	101 cm
A	188 cm	147 cm	101 cm
B	211 cm	148 cm	101 cm
C	227 cm	155 cm	101 cm
D	274 cm	157 cm	101 cm

Interval conversions - Frequency ratio to cents and vice versa

Frequency domain of musical instruments, singing voices (vocals), and keyboards

Vocal range:

Pitch	Start	End
Bass	82 Hz	349 Hz
Bariton	89 Hz	392 Hz
Tenor	131 Hz	494 Hz
Alt	175 Hz	699 Hz
Soprano	247 Hz	1175 Hz

... and showing the keyboard, and the note names.

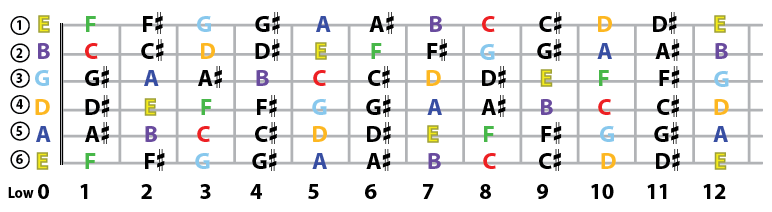
Guitar Fret Board with Notes

MIDI note numbers (midi files)

Octave notation is given here in the international standard ISO system, formerly known as
the ASA (Acoustical Society of America) or ANSI system. In this system, middle C (MIDI
note number 60) is C4; octaves start with C, so the B just below (MIDI number 59) is B3.
The lowest note of the normal modern piano is A0 (MIDI 21), though Boesendorfer
Imperials go down to F0 or even C0. The highest note of the piano is C8 (MIDI 108).

Octave #	MIDI Note Numbers
Octave #	C	C#	D	D#	E	F	F#	G	G#	A	A#	B
−1	0	1	2	3	4	5	6	7	8	9	10	11
0	12	13	14	15	16	17	18	19	20	21	22	23
1	24	25	26	27	28	29	30	31	32	33	34	35
2	36	37	38	39	40	41	42	43	44	45	46	47
3	48	49	50	51	52	53	54	55	56	57	58	59
4	60	61	62	63	64	65	66	67	68	69	70	71
5	72	73	74	75	76	77	78	79	80	81	82	83
6	84	85	86	87	88	89	90	91	92	93	94	95
7	96	97	98	99	100	101	102	103	104	105	106	107
8	108	109	110	111	112	113	114	115	116	117	118	119
9	120	121	122	123	124	125	126	127

Note: The MIDI specification only defines note number 60 as "Middle C", and all
other notes are relative. The absolute octave number designations shown here
are based on Middle C = C4, which is an arbitrary assignment.

Method for finding the corresponding MIDI note number for a given frequency:
Original expression f = 440 × 2^{(n − 69) / 12}
Simplification step 1: f / 440 = 2^{(n − 69) / 12}
Simplification step 2: log₂ (f / 440) = (n − 69) / 12
Simplification step 3: 12 × log₂ (f / 440) = n – 69

Formula for finding a MIDI note number given the frequency in Hz of the MIDI note:
n = (12 × log₂ (f / 440)) + 69
Given the frequency f for a note in Hz, it is possible to find the corresponding MIDI
note number represented by the variable n.

One version of the MIDI system uses C3 to designate Middle C (MIDI note 60 = 261.626 Hz).
That means that the octave designation for MIDI note "0" would be "-2" or notated as C-2.
Another version of the MIDI system uses the lowest note available to the MIDI system.
MIDI note 1 = 8.176 Hz to designate Octave "0" with the notation of C0.
"Middle C" is the MIDI note 60 = 261.626 Hz. That is octave 4 with the notation of C4.

MIDI Notes and their corresponding frequencies

The frequency 261.626 Hz = C4 (middle C),
and not C5 or C3, how some firms try to explain us; look at:
http://www.music.vt.edu/musicdictionary/appendix/octaveregisters/octaveregisters.html

Note	MIDI	Hz	Note	MIDI	Hz	Note	MIDI	Hz	Note	MIDI	Hz
C -	0	8.176	G# 1	32	51.913	E 4	64	329.63	C 7	96	2093.0
C# -	1	8.662	A 1	33	55.000	F 4	65	349.23	C# 7	97	2217.5
D -	2	9.177	A# 1	34	58.270	F# 4	66	369.99	D 7	98	2349.3
D# -	3	9.723	B 1	35	61.735	G 4	67	391.99	D# 7	99	2489.0
E -	4	10.301	C 2	36	65.406	G# 4	68	415.31	E 7	100	2637.0
F -	5	10.913	C# 2	37	69.295	A 4	69	440.00	F 7	101	2793.8
F# -	6	11.562	D 2	38	73.416	A# 4	70	466.16	F# 7	102	2960.0
G -	7	12.250	D# 2	39	77.781	B 4	71	493.88	G 7	103	3136.0
G# -	8	12.978	E 2	40	82.406	C 5	72	523.25	G# 7	104	3322.4
A -	9	13.750	F 2	41	87.307	C# 5	73	554.37	A 7	105	3520.0
A# -	10	14.568	F# 2	42	92.499	D 5	74	587.33	A# 7	106	3729.3
B -	11	15.434	G 2	43	97.998	D# 5	75	622.25	B 7	107	3951.1
C 0	12	16.352	G# 2	44	103.82	E 5	76	659.26	C 8	108	4186.0
C# 0	13	17.324	A 2	45	110.00	F 5	77	698.46	C# 8	109	4434.9
D 0	14	18.354	A# 2	46	116.54	F# 5	78	739.99	D 8	110	4698.6
D# 0	15	19.445	B 2	47	123.47	G 5	79	783.99	D# 8	111	4978.0
E 0	16	20.601	C 3	48	130.81	G# 5	80	830.61	E 8	112	5274.0
F 0	17	21.826	C# 3	49	138.59	A 5	81	880.00	F 8	113	5587.7
F# 0	18	23.124	D 3	50	146.83	A# 5	82	932.32	F# 8	114	5919.9
G 0	19	24.499	D# 3	51	155.56	B 5	83	987.77	G 8	115	6271.9
G# 0	20	25.956	E 3	52	164.81	C 6	84	1046.5	G# 8	116	6644.9
A 0	21	27.50	F 3	53	174.61	C# 6	85	1108.7	A 8	117	7040.0
A# 0	22	29.135	F# 3	54	184.99	D 6	86	1174.7	A# 8	118	7458.6
B 0	23	30.867	G 3	55	195.99	D# 6	87	1244.5	B 8	119	7902.1
C 1	24	32.703	G# 3	56	207.65	E 6	88	1318.5	C 9	120	8372.0
C# 1	25	34.648	A 3	57	220.00	F 6	89	1396.9	C# 9	121	8869.8
D 1	26	36.708	A# 3	58	233.08	F# 6	90	1480.0	D 9	122	9397.3
D# 1	27	38.890	B 3	59	246.94	G 6	91	1568.0	D# 9	123	9956.1
E 1	28	41.203	C 4	60	261.63	G# 6	92	1661.2	E 9	124	10548.1
F 1	29	43.653	C# 4	61	277.18	A 6	93	1760.0	F 9	125	11175.3
F# 1	30	46.249	D 4	62	293.66	A# 6	94	1864.7	F# 9	126	11839.8
G 1	31	48.999	D# 4	63	311.13	B 6	95	1975.5	G 9	127	12543.9

Frequency to Musical Note Converter
Find out what musical note a given frequency is. English system.

The frequency of 440 Hz is the concert pitch note A4.
If someone tells you different, this person is in error.

Since 1939 in many countries the valid standard pitch is set at
A4 = 440 Hz. In German and Austrian symphony orchestras,
however, a tuning for A4 = 443 Hz is common.
In Switzerland it is A4 = 442 Hz. Herbert von Karajan tuned his
Berlin Philharmonic Orchestra at A4 = 444 Hz.
That is however, not the standard pitch.

Overtones, partials and harmonics from fundamental frequency

Frequency domain of musical instruments, singing voices (vocals), and keyboards

Conversions of Intervals - Frequency ratio to cents and cents to frequency ratio

[top of page]

back

Search Engine

home