

| Deutsche Version |
| In acoustics the basic vibration is the 'first harmonic'. The term overtone is used to refer to any resonant frequency above the fundamental frequency. |
| The 'second harmonic' (twice the fundamental frequency) is the first overtone. Persons who count differently are wrong. In counting − harmonics are not overtones. |
|
There are integer multiples of a certain frequency (fundamental), that are called
harmonics, partial tones (partials) or overtones. It is important to note that the
term 'overtones' does not include the fundamental frequency. The first overtone is
therefore already the second harmonic or the second partial. The term overtone
should never be mixed with the other terms, as the counting is unequal. The term harmonic has a precise meaning - that of an integer (whole number) multiple of the fundamental frequency of a vibrating object. A harmonic frequency is a multiple of a fundamental frequency, also called "harmonic". Especially when it comes to counting, do not say: "overtones are harmonics". Musicians prefer the term overtones and physicists prefer the term harmonics. Sound engineers are somewhat uncertain between these two terms. Harmonics and overtones are also called resonant frequencies. |
|
| Comparison to fundamental |
Interval to previous tone |
Frequency ratio |
Tone example |
Frequency in Hz |
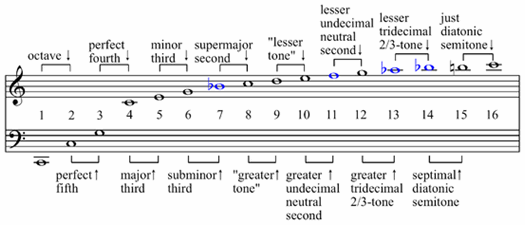
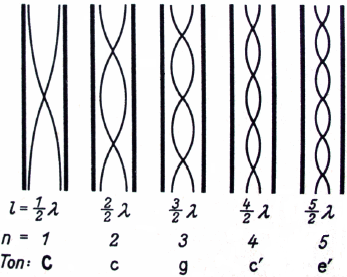
| fundamental frequency | fundamental | 1:1 | C | 65 |
| double frequency | octave | 2:1 | c | 130 |
| trifold frequency | fifth | 3:2 | g | 195 |
| fourfold frequency | fourth | 4:3 | c' | 260 |
| fivefold frequency | major third | 5:4 | e' | 325 |
| sixfold frequency | minor third | 6:5 | g' | 390 |
| sevenfold frequency | 7:6 | natural seventh | 455 | |
| eightfold frequency | 8:7 | c'' | 520 | |
| ninefold frequency | large whole tone | 9:8 | d'' | 585 |
| tenfold frequency | small whole tone | 10:9 | e'' | 650 |
| elevenfold frequency | 11:10 | alphorn F5 | 715 | |
| twelvefold frequency | 12:11 | g'' | 780 | |
| thirteenfold frequency | 13:12 | 845 | ||
| fourteenfold frequency | 14:13 | 910 | ||
| fifteenfold frequency | 15:14 | b'' | 975 | |
| sixteenfold frequency | minor second | 16:15 | c''' | 1040 |
| The frequency ratio results in a natural tone series, not related to the equal stretched temperament. |
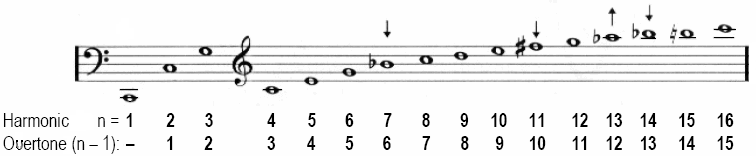
| Harmonics | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Partials | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Overtones | Fundamental | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Frequency | f | 2·f | 3·f | 4·f | 5·f | 6·f | 7·f | 8·f | 9·f | 10·f | 11·f | 12·f | 13·f | 14·f | 15·f | 16·f |
| Example Hz | 65 | 130 | 195 | 260 | 325 | 390 | 455 | 520 | 585 | 650 | 715 | 780 | 845 | 910 | 975 | 1040 |
| Tone name | C2 | C3 | G3 | C4 | E4 | G4 | Bb4 | C5 | D5 | E5 | F#5 | G5 | Ab5 | Bb5 | B5 | C6 |
| gray = even-numbered harmonics, (1f), 2f, 4f, 6f..., e.g. triode valve (tube) and
white = odd-numbered harmonics, 1f, 3f, 5f..., e.g. organ pipe closed at top
and clarinet all integer harmonics, e.g. saw tooth wave. The frequency spectrum of a symmetric square wave signal (pulse-pause ratio of 1:1) has exclusively odd-numbered harmonics of 3, 5, 7… or even-numbered overtones 2, 4, 6… The sound spectra of clarinets tend to have strong odd harmonics (fundamental, 3rd, 5th, 7th etc) and weak even harmonics (2nd, 4th, 6th etc), at least in their lowest registers. Tympanic membranes or bells have a large number of individual vibrations, which are not simply the exact multiples of single fundamental frequency. These are not harmonic overtones and are often called partial tones or partials. Overtones whose frequencies are not an integer multiple of the fundamental are called inharmonic and are often perceived as unpleasant. Inharmonics are not the same as Enharmonics. Bells have more clearly perceptible partials than most instruments. An "exciter" is a special equalizer, which creates new overtones. The processed signal is added to the original input signal. |
 |
| |||
| Even-numbered harmonics | Odd-numbered harmonics | |||
| are odd-numbered overtones | are even-numbered overtones |
| Typical "warm" tube sound, particularly triodes contain predominantly in the spectrum even-numbered multiples of the fundamental frequency, and thus outstanding even-numbered harmonics, or even-numbered partial tones 2, 4, 6… One can also say, tube amplifiers at high levels (distortion) contain strong odd-numbered overtones - that are even-numbered partials or harmonics. Organ pipes closed at the top (gedackt), which are half as long as open organ pipes of the same pitch, have a slightly dull and hollow sound. The spectrum shows predominantly odd-numbered multiples of the fundamental frequency and thus outstanding odd-numbered harmonics, or odd-numbered partial tones 3, 5, 7… One can also say, closed, covered, stopped organ pipes, and also the clarinet contains mostly even-numbered overtones - that are odd-numbered partials or harmonics. Because a clarinet acts like a closed tube resonator, it theoretically produces only odd-numbered harmonics, that are even-numbered overtones. But there are also some even-numbered harmonics content; look at: http://www.phys.unsw.edu.au/jw/clarinetacoustics.html#harmonics |
|
Notice: All harmonics are overtones is correct, but . . . Even-numbered overtones are odd-numbered harmonics, or partial tones. Odd-numbered overtones are even-numbered harmonics, or partial tones. Harmonics do not have the same counting like the overtones. Do not mix overtones with harmonics. It is recommended to mention odd and even multiples of the fundamental frequency, because that coincides with the counting of the harmonics and the partial tones, and if possible avoid the mention of even and odd overtones, which have a different counting, what shows often typical errors. Avoid the word combination "harmonic overtones". |
 |
| The predominant odd-numbered harmonics or alternatively even-numbered overtones of a clarinet The 2nd and the 4 the harmonic are very weak, but important |
Courtesy of Joe Wolfe: http://www.phys.unsw.edu.au/jw/flutes.v.clarinets.html
The words "odd-numbered overtones" are not correct for a clarinet.
Only even overtones or odd harmonics are right here.
| What is the right answer? Which typical overtones are found in a clarinet in addition to the fundamental? ● Even overtones 2, 4 and 6 or odd harmonics 3, 5, and 7? Which typical harmonics are found in a clarinet in addition to the fundamental? Odd harmonics 3, 5 and 7 or even overtones 2, 4, and 6? Which "melodious" overtones are produced by a triode electode tube in addition to the fundamental with a slight overdrive (distortion)? ● Odd overtones 1, 3 and 5 or even harmonics 2, 4, and 6? Which "melodious" harmonics are produced by a triode electrode tube in addition to the fundamental with a slight overdrive (distortion)? Even harmonics 2, 4 and 6 or odd overtones 1, 3, and 5? No wonder that in books and on the Internet many of these statements are rather unwisely. One should have his head quite clear in thinking, and looking at the figure above. |
|
Clarinets odd harmonics 1 3 5 7 9 11 Flutes even harmonics 2 4 6 8 10 12 14 16 18 |
|
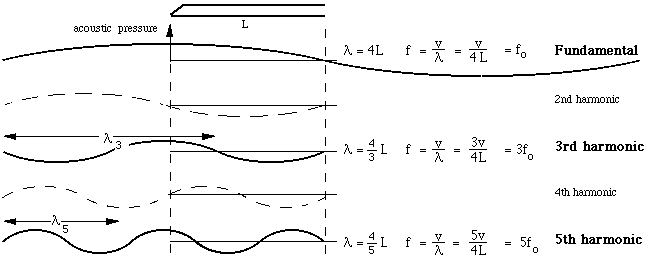
Length calculation for an open pipe:
Length calculation for a closed pipe: |
Frequency of concert pitch A4 and the counting of harmonics and overtones
| Frequency | Order | Harmonics | Overtones |
| 1 × f = 440 Hz | n = 1 | 1st (odd) harmonic | fundamental |
| 2 × f = 880 Hz | n = 2 | 2nd (even) harmonic | 1st (odd) overtone |
| 3 × f = 1320 Hz | n = 3 | 3rd (odd) harmonic | 2nd (even) overtone |
| 4 × f = 1760 Hz | n = 4 | 4th (even) harmonic | 3rd (odd) overtone |
| 4 × f = 2200 Hz | n = 5 | 5th (odd) harmonic | 4th (even) overtone |
| Symmetrical amplifier push/pull circuits must cancel even order harmonics, like 2, 4, 6… and therefore promote odd order harmonics, like 1, 3, 5… when driven into the nonlinear range. |
| Brass instruments: trumpet, baritone horn, trombone, flugelhorn, cornet, tenor horn (alto horn), horn, euphonium, tuba, bass tuba, cimbasso, alphorn, conch, didgeridoo, natural horn, keyed bugle, keyed trumpet, serpent, ophicleide, shofar, vladimirskiy rozhok, vuvuzela |
 |
| "Open ends" displacement "Fixed ends" |
 fn = c / λn = n · f1 = n · c / (2 L) |
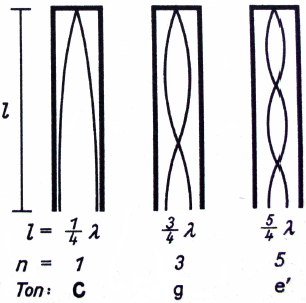 fn = (2n − 1) · f1 = (2n − 1) · c / (4 L) |
| Open pipe with all harmonics or also with all overtones |
Closed pipe with unevenharmonics and therefore only with even overtones |
| In figures of waves is almost never indicated whether the pressure variations
in the air (sound pressure) or the displacement of the air particles
is meant. Here you see the displacement. Notice: To a sound displacement node a sound pressure antinode corresponds. The effect of waves reports our hearing, but only the sound pressure deviations (fluctuations, variations) move effectively our eardrums. |
| back |
Search Engine |
home |