

| English version |

Fülle das Feld oben aus und klicke auf die jeweilige Berechnungs-Taste darunter.
Frequenz bedeutet Schwingungen pro Sekunde in Hertz = Hz = 1/s.
1 Sekunde = 1 s = 1000 ms | 1 ms = 0,001 s | 1 µs = 0,000001 s.
 |
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Oszilloskop: Eingabe der Kästchen (Div.) und der Timebase (Y) ergibt die Frequenz.
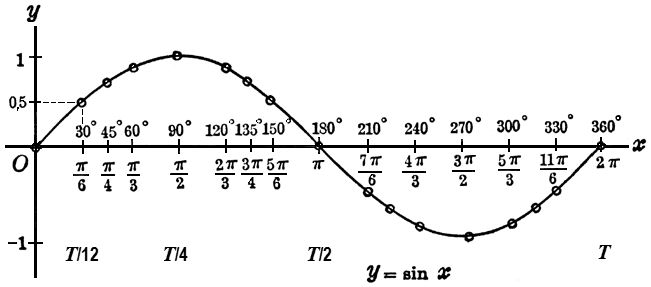
Formel für die Periode T
| Physikalische Größe | Formelzeichen | Maßeinheit | Abkürzung | Formel |
| Periode (Dauer) | T = 1 / f | Sekunde | s | T = λ / c |
| Frequenz | f = 1 / T | Hertz | Hz = 1/s | f = c / λ |
| Wellenlänge | λ | Meter | m | λ = c / f |
| Schallgeschwindigkeit | c | Meter pro Sekunde | m/s | c = λ · f |
| Berechnung von Frequenz in Wellenlänge und zurück Berechnung von Schallgeschwindigkeit aus der Temperatur |
 |
| In der Physik und der Elektrotechnik wird für sinusförmige Vorgänge häufig die Kreisfrequenz ω anstatt der Frequenz f benutzt. Die Drehzahl oder Umdrehungsfrequenz ist eine Größe, die bei − vorzugsweise mechanischen − Drehbewegungen die Häufigkeit der Umdrehungen angibt. Sie ist beispielsweise ein wesentliches Kennzeichen für Motoren. Sie wird in 1/s, als Umdrehungen pro Minute oder auf Englisch in rpm als "revolutions per minute" angegeben. |
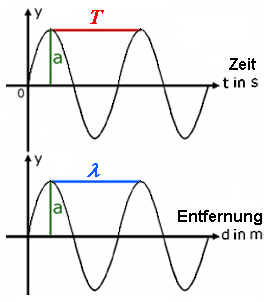 |
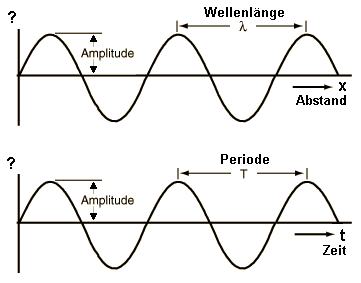
| Die y-Achse zeigt den Schalldruck p (Schalldruckamplitude). Wenn die Abbildung auf der x-Achse die Zeit t zeigt, dann sehen wir die Periodendauer T = 1 / f. Wenn die Abbildung auf der x-Achse den Abstand d zeigt, dann sehen wir die Wellenlänge λ. Die größte Auslenkung oder Elongation wird mit Amplitude a bezeichnet. |
| Die Amplitude hat absolut nichts mit der Frequenz zu tun ... und auch nichts mit der Wellenlänge. |
 |
| In der Akustik hat der Ausdruck für eine Sinuswelle die Form: y = A sin (2 π f T + φ). Wobei ω = 2 π f und A die Amplitude ist und f die Frequenz der Welle gemessen in Hertz. Die mathematische Form ist: y = A sin (B T + φ). Wir erkennen hierbei, dass | B | = 2 π f ist. Daher ist die Frequenz f = | B | / 2 π unddie Periodendauer T = 2 π / | B | = 1 / f. |
| Harmonische, Obertöne und Teiltöne aus der Grundfrequenz Klaviatur, Frequenzen = Notennamen, Piano-Tastatur Frequenzbereich der Musikinstrumente und Gesangsstimmen |
| SI-Präfixe für Hertz (Hz) nach DIN 1301 | ||||||
| Wert | Symbol | Name | Wert | Symbol | Name | |
| 10−1 Hz | dHz | Dezihertz | 101 Hz | daHz | Dekahertz | |
| 10−2 Hz | cHz | Zentihertz | 102 Hz | hHz | Hektohertz | |
| 10−3 Hz | mHz | Millihertz | 103 Hz | kHz | Kilohertz | |
| 10−6 Hz | µHz | Mikrohertz | 106 Hz | MHz | Megahertz | |
| 10−9 Hz | nHz | Nanohertz | 109 Hz | GHz | Gigahertz | |
| 10−12 Hz | pHz | Pikohertz | 1012 Hz | THz | Terahertz | |
| 10−15 Hz | fHz | Femtohertz | 1015 Hz | PHz | Petahertz | |
| 10−18 Hz | aHz | Attohertz | 1018 Hz | EHz | Exahertz | |
| 10−21 Hz | zHz | Zeptohertz | 1021 Hz | ZHz | Zettahertz | |
| 10−24 Hz | yHz | Yoktohertz | 1024 Hz | YHz | Yottahertz | |
| Die üblichen Einheiten sind dick gedruckt. | ||||||
Eine typische Frage: Wie ist die Beziehung zwischen Wellenlänge, Temperatur und Frequenz?
| Erkläre die Beziehung zwischen Entfernung, Zeit und Frequenz um die Wellenänge zubestimmen oder: Wie lautet die Gleichung mit Frequenz, Entfernung und Zeit? Entfernung ist auch Abstand oder Distanz. Geschwindigkeit = Entfernung / Zeit Geschwindigkeit = Wellenlänge × Frequenz deshalb: Wellenlänge × Frequenz = Entfernung / Zeit deshalb: Wellenlänge = Entfernung / (Zeit × Frequenz) |
![]()
Masterclock-Rechner (Taktfrequenz)
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
Klaviatur, Frequenzen, Notennamen und Piano-Tastatur
Berechnen der Harmonischen aus der Grundfrequenz
![]()
Rechner mit Eingabe der Referenz-Frequenz
100 cent entsprechen einem Halbton.
Für Abwärtsstimmung kann Referenz-Frequenz und Flügelstimmung getauscht werden.
Klaviatur, Frequenzen, Notennamen und Piano-Tastatur
Berechnen der Harmonischen aus der Grundfrequenz
![]()
| zurück |
Suchmaschine |
Startseite |